•Article•6 months ago

Binomial coefficient

A combination of $n$ elements taken $k$ at a time is a set of $k$ elements chosen from the given $n$ elements. In this context, sets that differ only in the order of the elements (but not in their composition) are considered identical. It is precisely this property of combinations that distinguishes them from permutations.

For example, consider a set of $5$ elements: ${1, 2, 3, 4, 5}$ . The sets ${2, 1, 3}$ and ${3, 2, 1}$ are identical as combinations (though different as permutations) because they consist of the same elements ${1, 2, 3}$ .

The formula for calculating the number of combinations of $n$ elements taken $k$ at a time is

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!}

The numbers $C_{n}^{k}$ are called binomial coefficients.

When we choose zero elements from a set of $n$ elements, we are essentially making an “empty” choice. The empty set, in this context, is considered a valid combination. Imagine you have a box with $n$ balls, and you want to choose $0$ of them. Even if you don’t choose anything, it is still a valid choice. Thus, $C_{n}^{0}$ is the number of ways to choose $0$ elements from $n$ , which is equal to $1$ .

We can think of this as the one and only way to not choose any elements from the set, which gives the result of $1$ .

C_{n}^{0} = \frac{n !}{0 ! \cdot ( n - 0 )!} = \frac{n !}{1 ! \cdot n !} = 1

When we choose one element from a set of $n$ elements, we have $n$ options to choose from: we can choose any one of the $n$ elements. For example, if we have a set of numbers from $1$ to $5$ ( ${1, 2, 3, 4, 5}$ ), we can choose one number from this set, and we have $5$ options for this choice.

The value $C_{n}^{1}$ equals $n$ because there are $n$ ways to choose one element from a set of $n$ elements.

C_{n}^{1} = \frac{n !}{1 ! \cdot ( n - 1 )!} = n

When choosing $2$ elements from a set of $n$ elements, we form combinations of pairs. To build such a pair, we first choose one element, and then the second.

The first element can be chosen from $n$ elements.
After choosing the first element, we have $n -1$ elements left to choose the second element (since we cannot choose the same element again).

Thus, the total number of combinations of pairs of elements that can be chosen from a set of $n$ elements is the product of the number of ways to choose the first and second elements: $n \cdot (n -1)$ .

However, each pair is counted twice, as the order of elements in the pair does not matter. For example, $(p, q)$ and $(q, p)$ are considered the same pair. To account for this, the total number of combinations should be divided by $2$ . Therefore, the value $C_{n}^{2}$ equals $n \cdot (n -1) /2$ .

C_{n}^{2} = \frac{n !}{2 ! \cdot ( n - 2 )!} = \frac{n \cdot ( n - 1 )}{2}

Symmetry rule: $C_{n}^{k} = C_{n}^{n - k}$ .

The number of ways to choose $k$ elements from $n$ is equal to the number of ways to not choose $(n - k)$ elements from $n$ . There are $C_{n}^{n - k}$ ways to not choose $(n - k)$ elements from $n$ . Therefore $C_{n}^{k} = C_{n}^{n - k}$ .

Exercise. Calculate the values of the following binomial coefficients:

1) $C_{5}^{2}$	3) $C_{5}^{4}$	5) $C_{8}^{1}$
2) $C_{8}^{3}$	4) $C_{7}^{5}$	6) $C_{8}^{5}$

Summation formula: $C_{n}^{k} = C_{n - 1}^{k - 1} + C_{n - 1}^{k}$ .

Proof. Let’s calculate the value of the right-hand side of the equation:

C_{n - 1}^{k - 1} + C_{n - 1}^{k} = \frac{( n - 1 )!}{( k - 1 )! \cdot ( n - k )!} + \frac{( n - 1 )!}{k ! \cdot ( n - k - 1 )!} =

\frac{( n - 1 )! \cdot k + ( n - 1 )! \cdot ( n - k )}{k ! \cdot ( n - k )!} = \frac{( n - 1 )! \cdot ( k + n - k )}{k ! \cdot ( n - k )!} = \frac{n !}{k ! \cdot ( n - k )!} = C_{n}^{k}

Preparing for the calculus exam, Petya spread out $n$ different cheat sheets in front of himself. They were his salvation, as throughout the entire semester Petya had never bothered to properly study the material. There were so many cheat sheets that they didn’t fit into any pocket. Therefore, Petya decided to calculate the maximum number of cheat sheets he could take with him to the exam. And then the question arose: how many ways are there in total to choose the required number of cheat sheets?

Input. Contains the total number of cheat sheets $n (1 \leq n \leq 12)$ and the number of cheat sheets $k (0 \leq k \leq n)$ that Peter can take with him.

Output. Print the number of ways to choose $k$ cheat sheets from $n$ .

Open problem

Binomial coefficients appear in Newton’s binomial:

(x + y)^{n} = k = 0 \sum n C_{n}^{k} x^{k} y^{n - k}

Let’s look at examples:

(x + y)^{2} = C_{2}^{0} x^{2} y^{0} + C_{2}^{1} x^{1} y^{1} + C_{2}^{2} x^{0} y^{2} = x^{2} + 2 x y + y^{2},

(x + y)^{3} = C_{3}^{0} x^{3} y^{0} + C_{3}^{1} x^{2} y^{1} + C_{3}^{2} x^{1} y^{2} + C_{3}^{3} x^{0} y^{3} = x^{3} + 3 x^{2} y + 3 x y^{2} + y^{3}

Let’s consider $2 n$ objects $a_{1}, ..., a_{2 n}$ and find the number of ways to select $n$ objects out of $2 n$ .

We’ll divide the set in half: ${a_{1}, a_{2}, ..., a_{n}, a_{n + 1}, ..., a_{2 n}}$ . To choose $n$ objects from $2 n$ , we’ll select $k (k \leq n)$ objects from the left half (from the set ${a_{1}, a_{2}, ..., a_{n}})$ and $n - k$ objects from the right half (from the set ${a_{n + 1}, a_{n + 2}, ..., a_{2 n}})$ . The number of ways to make such a selection, according to the rule of multiplication, is equal to $C_{n}^{k} \cdot C_{n}^{n - k} = (C_{n}^{k})^{2}$ . Since $k$ can take values from $0$ to $n$ , то $\sum_{k = 0}^{n} (C_{n}^{k})^{2}$ is equal to the number of ways to choose $n$ objects from $2 n$ , which is equal to $C_{2 n}^{n}$ . Thus,

(C_{n}^{0})^{2} + (C_{n}^{1})^{2} + (C_{n}^{2})^{2} + ... + (C_{n}^{n})^{2} = C_{2 n}^{n}

Example

For $n = 3$ the answer is $(C_{3}^{0})^{2} + (C_{3}^{1})^{2} + (C_{3}^{2})^{2} + (C_{3}^{3})^{2} = 1^{2} + 3^{2} + 3^{2} + 1^{2} = 20$

At the same time $C_{6}^{3} = \frac{6 !}{3 ! \cdot 3 !} = \frac{4 \cdot 5 \cdot 6}{6} = 20$ .

Computations will be performed using $64$ -bit unsigned integers (unsigned long long). Its obvious that

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!} = \frac{n \cdot ( n - 1 ) \cdot ( n - 2 ) \cdot ... \cdot ( n - k + 1 )}{1 \cdot 2 \cdot 3 \cdot ... \cdot k} = \frac{n}{1} \cdot \frac{n - 1}{2} \cdot \frac{n - 2}{3} \cdot ... \cdot \frac{n - k + 1}{k}

Let’s assign the value of the variable $res$ to $1$ . Then multiply it by $\frac{n - i + 1}{i}$ for all $i$ from $1$ to $k$ . Each time the division by $i$ will yield an integer result, but multiplication can cause overflow. Let $d = GC D (res, i)$ . Then let’s rewrite the operation

res = res * (n - i + 1) / i

res = (res / d) * ((n - i + 1) / (i / d))

In this implementation we’ll avoid overflow (the answer is $64$ -bit unsigned integer). Note that first we need to perform the division $(n - i + 1) / (i / d)$ , and then multiply $res / d$ by the resulting quotient.

To compute $C_{n}^{k}$ , we must run $k$ iterations. But what to do if we want to compute $C_{2000000000}^{1999999999}$ ? The answer is no more than $2^{64}$ , so such input values are possible. As long as $C_{n}^{k} = C_{n}^{n - k}$ , then for $n - k < k$ we should assign $k = n - k$ .

Example

Consider the next sample:

C_{6}^{3} = \frac{6}{1} \cdot \frac{5}{2} \cdot \frac{4}{3} = 15 \cdot \frac{4}{3}

Let $res = 15$ , and we need to make a multiplication $res \cdot \frac{4}{3} = 15 * \frac{4}{3}$ . Compute $d = GC D (15, 3) = 3$ . So $15 \cdot \frac{4}{3} = (15/3) \cdot \frac{4}{3/3} = 5 \cdot \frac{4}{1} = 20$ .

Rewrite the sum in the form:

1 \cdot C_{n}^{0} + 2 \cdot C_{n}^{1} + 3 \cdot C_{n}^{2} + ... + (n + 1) \cdot C_{n}^{n} =

(C_{n}^{0} + C_{n}^{1} + C_{n}^{2} + ... + C_{n}^{n}) + 1 \cdot C_{n}^{1} + 2 \cdot C_{n}^{2} + ... + n \cdot C_{n}^{n}

The sum in parentheses is $2^{n}$ . If in Newton’s binomial formula

(a + b)^{n} = i = 0 \sum n C_{n}^{i} a^{i} b^{n - i}

we set $a = b = 1$ , then we get the relation: $(1 + 1)^{n} = \sum_{i = 0}^{n} C_{n}^{i} 1^{i} 1^{n - i}$ , or

2^{n} = i = 0 \sum n C_{n}^{i} = C_{n}^{0} + C_{n}^{1} + ... + C_{n}^{n}

Let’s compute the remaining sum:

1 \cdot C_{n}^{1} + 2 \cdot C_{n}^{2} + ... + n \cdot C_{n}^{n} =

1 \cdot \frac{n !}{1 ! \cdot ( n - 1 )!} + 2 \cdot \frac{n !}{2 ! \cdot ( n - 2 )!} + ... + n \cdot \frac{n !}{n ! \cdot ( n - n )!} =

n \cdot (\frac{( n - 1 )!}{0 ! \cdot ( n - 1 )!} + \frac{( n - 1 )!}{1 ! \cdot ( n - 2 )!} + ... + \frac{( n - 1 )!}{( n - 1 )! \cdot ( n - n )!}) =

n \cdot (C_{n - 1}^{0} + C_{n - 1}^{1} + ... + C_{n - 1}^{n - 1}) = n \cdot 2^{n - 1}

So the answer is $2^{n} + n \cdot 2^{n - 1} = (n + 2) \cdot 2^{n - 1}$ .

Example

Compute the value for $n = 3$ . For direct calculation:

1 \cdot C_{3}^{0} + 2 \cdot C_{3}^{1} + 3 \cdot C_{3}^{2} + 4 \cdot C_{3}^{3} = 1 \cdot 1 + 2 \cdot 3 + 3 \cdot 3 + 4 \cdot 1 = 1 + 6 + 9 + 4 = 20

When calculated using the formula: $5 \cdot 2^{2} = 20$ .

You have a piece of paper and you choose a rectangle of size $n \cdot m$ on it. Let’s call this rectangle together with the lines it contains a grid. Starting at the lower left corner of the grid, you move your pencil to the upper right corner, taking care that it stays on the lines and moves only to the right or up. The result is shown on the left:

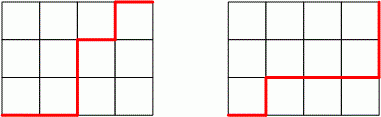
Really a masterpiece, isn’t it? Repeating the procedure one more time, you arrive with the picture shown on the right. Now you wonder: how many different works of art can you produce?

Input. Two positive integers $n$ and $m$ .

Output. Print the number of different art works that can be generated using the procedure described above. You may safely assume that this number fits into a $64$ -bit signed integer.

Open problem

Gunnar is quite an elderly and forgetful researcher. Currently, he is writing a paper on security in social networks that involves some combinatorics. He developed a program to calculate binomial coefficients to assist him in verifying some of his calculations.

The binomial coefficient $C_{n}^{k}$ is a number defined by

C_{n}^{k} = \frac{n !}{k ! \cdot ( n - k )!}

where $n$ and $k$ are non-negative integers.

Gunnar uses his program to calculate $C_{n}^{k}$ and obtains a number $m$ as a result. Unfortunately, being forgetful, he forgot the numbers of $n$ and $k$ he used as input. These two numbers were the result of lengthy computations and were written on one of the many sheets scattered across his desk. Instead of searching through the papers, he decided to reconstruct the numbers $n$ and $k$ from the obtained answer. Can you help him find all possible values?

Input. The first line contains the number of test cases, at most $100$ . Each test is given in a single line and contains an integer $m (2 \leq m \leq 1 0^{15})$ — the result of the Gunnar’s program.

Output. For each test, print two lines. The first line should contain the number of ways to express $m$ using the binomial coefficient. The second line should contain all pairs $(n, k)$ such that $C_{n}^{k} = m$ . Pairs should be sorted in increasing order of $n$ , and in case of equality, in increasing order of $k$ . The output format of pairs is given in the example.

Open problem

If $C_{n}^{k} = m$ , then $C_{n}^{n - k} = m$ . It is sufficient to find the solution for $k \leq n /2$ and, along with the pair $(k, n)$ , also print the pair $(k, n - k)$ . For $k = n /2$ these two pairs coincide.

Let $p$ be the smallest number for which $C_{2 p}^{p} > m$ . Then it is obvious that $0 \leq k < p$ .

Choose $k$ such that $C_{2 k}^{k} \leq m$ and consider the function $f (n) = C_{n}^{k}$ . Then for $2 k \leq n \leq m$ , the function $f (n)$ is monotonically increasing. Therefore, you can solve the equation $f (n) = m$ by binary search.

To solve the problem, one should iterate over the values of $k (0 \leq k < p)$ , and for each such $k$ , solve the equation $C_{n}^{k} = m$ relatively $n$ with binary search. The found value of $n$ must be an integer.

Example

Consider the equation $C_{n}^{k} = 3003$ . Given that $C_{12}^{6} = 924$ and $C_{14}^{7} = 3432$ , it is sufficient to iterate over $0 \leq k \leq 6$ .

Let $k = 2$ , consider the equation $C_{n}^{2} = 3003$ or $\frac{n \cdot ( n - 1 )}{2} = 3003$ , $n \cdot (n -1) = 6006$ . By binary search in the interval $4 \leq n \leq 3003$ , we find an integer solution $n = 78$ . Since $n \neq = 2 \cdot k$ , we have two solutions: $C_{78}^{2} = C_{78}^{76} = 3003$ .

Store the required pairs in the vector of pairs $res$ .

vector<pair<long long,long long> > res;

The Cnk function computes the value of binomial coefficient $C_{n}^{k}$ .

long long Cnk(long long n, long long k)
{
  long long i, Res = 1;
  if (k > n - k) k = n - k;
  for(i = 1; i <= k; i++)
  {

If at the next iteration the result exceeds $m$ (we are searching for a solution to the equation $C_{n}^{k} = m$ ), then stop computations. Exiting the function at this point avoids overflow.

    if (1.0 * Res * (n - i + 1) / i > m) return m + 1;
    Res = Res * (n - i + 1) / i;
  }
  return Res;
}

The main part of the program. Read the input data.

scanf("%d",&tests);
while (tests--) 
{
  res.clear();
  scanf("%lld",&m);

Iterate over the values of $k$ from $0$ until $C_{2 k}^{k} \leq m$ .

  for(k = 0; Cnk(2*k,k) <= m; k++)
  {

Find the value of $n (2 k \leq n \leq m)$ using binary search.

    long long lo = 2*k, hi = m;
    while (lo < hi) 
    {
      long long n = (lo + hi) / 2;
      if (Cnk(n,k) < m) lo = n + 1; else hi = n;
    }

If $C_{l o}^{k} = m$ , then a solution is found. Include one or two pairs of solutions in the result.

    if (Cnk(lo,k) == m)
    {
      res.push_back(make_pair(lo,k));
      if (lo != 2*k)
        res.push_back(make_pair(lo,lo - k));
    }
  }

Sort the pairs.

  sort(res.begin(),res.end());

Print the answer — the number of found pairs and the pairs themselves.

  printf("%d\n",res.size());
  for(i = 0; i < res.size(); i++)
    printf("(%lld,%lld) ", res[i].first,res[i].second);
  printf("\n");
}

Asymptotic nonations for the Binomial Coefficients

Theorem 1. There exists a relationship between the binomial coefficients:

C_{n}^{0} < C_{n}^{1} < ... < C_{n}^{⌊ n /2 ⌋} \geq C_{n}^{⌊ n /2 ⌋ + 1} > ... > C_{n}^{n}

Theorem 2. $C_{2 n}^{n} < 4^{n}$ . Follows from the fact that $\sum_{k = 0}^{2 n} C_{2 n}^{k} = (1 + 1)^{2 n} = 2^{2 n} = 4^{n}$

Theorem 3. $C_{2 n}^{n} > \frac{4 ^{n}}{2 n + 1}$ . Follows from the fact that $\sum_{k = 0}^{2 n} C_{2 n}^{k} = 4^{n}$ , and the number of coefficients is $2 n + 1$ . Therefore, the largest of the coefficients will be greater than $\frac{4 ^{n}}{2 n + 1}$ .

Theorem 4. Stirling formula. $n! \approx 2 πn (\frac{n}{e})^{n}$ .

A more accurate approximation is:

n! \approx 2 πn (\frac{n}{e})^{n} (1 + \frac{1}{12 n} + \frac{1}{288 n ^{2}} - \frac{139}{51849 n ^{3}} - \frac{571}{2488320 n ^{4}})

Theorem 5.

C_{2 n}^{n} \approx \frac{4 πn ( \frac{2 n}{e} ) ^{2 n}}{( 2 πn ( \frac{n}{e} ) ^{n} ) ^{2}} = \frac{4 ^{n}}{πn}

Theorem 6.

C_{n}^{k} = \frac{n !}{k ! ( n - k )!} = \frac{n \cdot ( n - 1 ) \cdot ( n - 2 ) \cdot ... \cdot ( n - k + 1 )}{1 \cdot 2 \cdot 3 \cdot ... \cdot k} =

\frac{n !}{k !} \cdot (1 - \frac{1}{n}) \cdot (1 - \frac{2}{n}) \cdot ... \cdot (1 - \frac{k - 1}{n}) =

\frac{n !}{k !} \cdot e^{l n (1 - \frac{1}{n}) + l n (1 - \frac{2}{n}) + ... + l n (1 - \frac{k - 1}{n})} \leq (u se t h e in e q u a l i t y l n (1 - x) \leq - x)

\frac{n !}{k !} \cdot e^{- \frac{1}{n} - \frac{2}{n} - ... - \frac{k - 1}{n}} = \frac{n !}{k !} \cdot e^{- \frac{k \cdot ( k - 1 )}{2 n}}

List of problems

Comments

Nothing yet

Be the first one to start the conversation!

Loading

Just a moment, getting data from the server