•Article•5 months ago

Exploring recursion

The objective of this lesson is to introduce students to the concept of recursion, understanding its fundamentals, and mastering its implementation in programming. By the end of this lesson, students should be able to:

Define recursion and its key characteristics.
Understand the mechanics of recursive functions.
Implement basic recursive algorithms.
Identify scenarios suitable for recursion.

Introduction:

Begin with a brief discussion on problem-solving techniques in programming.
Introduce the concept of recursion with a real-life example.
Define recursion as a programming technique where a function calls itself directly or indirectly to solve a problem.
Highlight the key characteristics of recursion: base case, recursive case, and self-referentiality.

Understanding Recursive Functions:

Explain the mechanics of recursive functions using a simple example (factorial, power $x^{n}$ or Fibonacci sequence).
Demonstrate how recursive functions work step by step, emphasizing the importance of the base case.
Discuss the call stack and how it is used in recursive function calls.
Clarify the concept of infinite recursion and how to avoid it.

Implementing Recursive Algorithms:

Present a series of programming problems suitable for recursion.
Divide students into pairs or small groups to solve these problems using recursion.
Encourage students to write recursive functions from scratch, focusing on defining the base case and recursive case.
Circulate among groups to provide guidance and assistance as needed.

Review and Practice:

Have each group present their recursive solutions to the class.
Discuss the efficiency and readability of different recursive approaches.
Address any common challenges or misconceptions encountered during the exercise.
Provide additional practice problems for students to work on individually or in groups.

Conclusion:

Summarize the key points covered in the lesson, emphasizing the power and versatility of recursion in programming.
Encourage students to continue exploring recursion in their own projects and assignments.

Homework:

Assign homework exercises to reinforce the concepts learned in class, such as implementing recursive algorithms for specific problems or analyzing existing recursive functions in code libraries.

Assessment:

Assess student understanding through their participation in class discussions, their ability to solve recursive programming problems, and their clarity in explaining recursive solutions.
Review homework assignments to gauge individual mastery of recursion concepts and implementation skills.

Introduction

Begin with a brief discussion on problem-solving techniques in programming

In programming, problem-solving is a fundamental skill that you'll use every time you write code. Before we dive into the specifics of recursion, let's take a moment to talk about problem-solving techniques.

Think of problem-solving as a journey. You start with a problem — a task you want your program to accomplish — and you need to figure out how to get from point A (the problem) to point B (the solution). This journey involves breaking down the problem into smaller, more manageable pieces, understanding the rules or constraints involved, and devising a plan to reach the desired outcome.

There are several techniques that programmers use to tackle problems effectively. Here are a few key ones:

Understanding the Problem: Before you can solve a problem, you need to understand it fully. This involves reading and analyzing the problem statement, identifying the inputs and outputs, and clarifying any uncertainties.
Divide and Conquer: Many complex problems can be solved by breaking them down into smaller, more manageable subproblems. This approach, known as divide and conquer, allows you to tackle each subproblem separately and then combine the solutions to solve the larger problem.
Algorithmic Thinking: Algorithms are step-by-step procedures for solving problems. When you're faced with a problem, try to think algorithmically by breaking down the solution into a sequence of logical steps.
Abstraction: Abstraction involves focusing on the essential details of a problem while ignoring irrelevant or distracting information. By abstracting away unnecessary details, you can simplify the problem and concentrate on what's important.
Iteration and Recursion: Iteration involves solving a problem through repeated execution of a loop or sequence of instructions. Recursion, on the other hand, involves solving a problem by breaking it down into smaller instances of the same problem. Both iteration and recursion are powerful problem-solving techniques that you'll encounter frequently in programming.

By mastering these problem-solving techniques, you'll be better equipped to tackle a wide range of programming challenges, including those that involve recursion. So, as we explore recursion in more depth, keep these problem-solving strategies in mind — they'll serve as valuable tools in your programming toolbox.

Introduce the concept of recursion with a real-life example

Alright, let's take a step back from coding for a moment and think about recursion in terms of real-life examples. Imagine you're standing in front of a set of Russian nesting dolls, also known as Matryoshka dolls. These dolls come in various sizes, each fitting inside the next larger one.

Now, let's think about how we could describe the process of opening each doll in the set. You start with the largest doll, and as you open it, you find a smaller doll nested inside. You then open that smaller doll, only to discover an even tinier one inside, and so on, until you reach the smallest doll — the one that doesn't contain any others.

This process of opening each doll can be thought of as recursive. Why? Because each doll is similar in structure to the others, and the action of opening a doll is the same for each one – it involves looking inside to see if there's a smaller doll nested within.

In programming terms, recursion works in a similar way. Instead of opening Russian nesting dolls, we're "opening" functions or methods. A recursive function is one that calls itself, either directly or indirectly, to solve a problem by breaking it down into smaller instances of the same problem.

So, just like with the Matryoshka dolls, recursion involves tackling a problem by breaking it down into smaller, similar subproblems, until we reach a point where the problem is so small and simple that we can solve it directly. This smallest, simplest version of the problem is what we call the base case.

By understanding recursion through real-life examples like the Russian nesting dolls, we can begin to see how it applies to programming and how it can be a powerful tool for solving complex problems in a clear and elegant way. So, as we delve deeper into recursion, keep this visual analogy in mind — it'll help you grasp the concept more intuitively.

Define recursion as a programming technique where a function calls itself directly or indirectly to solve a problem

Now let's break down the definition of recursion into simpler terms. Imagine you have a function — a set of instructions that performs a specific task in your program. Now, what if I told you that this function could call itself? Yes, you heard that right! This is what we call recursion.

Recursion is like a loop, but instead of repeating a set of instructions until a condition is met, a recursive function repeats itself by calling itself — directly or indirectly — until it reaches a specific condition, usually called the base case.

Let me explain this with an example. Imagine you have a function called "countDown" that prints numbers from a given number $n$ down to $1$ . Instead of using a loop, we can define "countDown" recursively. Here's how it works:

The function "countDown" takes a number $n$ as input.
If the number is $1$ (the base case), it simply prints " $1$ " and stops.
If the number is greater than $1$ , it prints the current number and then calls itself with the next smaller number.
This process continues until the function reaches the base case, at which point it stops calling itself and the recursion "unwinds" back to the original call.

def countDown(n):
  # Base case: if n is 1, print it and stop recursion
  if n == 1:
    print(n)
  else:
    # Print current number
    print(n)
    # Call countDown function with the next smaller number
    countDown(n - 1)

# Example usage:
countDown(5)  # Prints numbers from 5 down to 1

So, in essence, recursion is a way of solving problems by breaking them down into smaller, similar subproblems, and then solving those subproblems by calling the same function again and again until we reach a base case where the problem can be solved directly.

Keep in mind that recursion can be a bit mind-bending at first, but with practice and understanding of its principles, you'll be able to wield it as a powerful tool in your programming arsenal.

Highlight the key characteristics of recursion: base case, recursive case, and self-referentiality

Now that we understand what recursion is and how it works, let's delve into its key characteristics. Recursion is like a well-oiled machine — it has specific parts that work together to make it function smoothly. Here are the three key characteristics of recursion that we'll highlight: base case, recursive case, and self-referentiality.

Base Case:

Think of the base case as the stopping point for our recursive function. It's the condition that tells the function when to stop calling itself and start returning values.
Without a base case, our recursive function would keep calling itself indefinitely, leading to what we call infinite recursion, which is not what we want!
In our earlier example of the "countDown" function, the base case was when $n$ became $1$ . At that point, we simply printed $1$ and stopped calling the function.

Recursive Case:

The recursive case is where the magic of recursion happens. It's the part of our function where we call the function itself.
Each time our function encounters the recursive case, it's like taking a step closer to the base case. We're breaking down the problem into smaller and smaller subproblems until we reach the base case.
In the "countDown" function, the recursive case was when $n$ was greater than $1$ . We printed the current value of $n$ , then called the "countdown" function again with $n -1$ .

Self-Referentiality:

This characteristic might sound fancy, but it's quite simple. Self-referentiality means that our function refers to itself.
When we define a recursive function, we're essentially saying, "Hey, function, you can call yourself if you need to."
This self-referential nature is what allows recursion to tackle complex problems by breaking them down into smaller instances of the same problem.
In the "countDown" function, we saw self-referentiality in action when we called countDown within the function itself.

So, to recap, recursion has three key characteristics:

the base case, which tells us when to stop;
the recursive case, which breaks down the problem into smaller subproblems;
self-referentiality, which allows the function to call itself.

Understanding and mastering these characteristics is essential for becoming proficient in recursion and using it effectively in your programming journey.

Understanding Recursive Functions

Explain the mechanics of recursive functions using a simple example

Let's break down the mechanics of recursive functions using the example of computing the factorial of a number.

The factorial of a non-negative integer $n$ , denoted as $n!$ , is the product of all positive integers less than or equal to $n$ . For example, $5!$ (read as "five factorial") is equal to $5 \cdot 4 \cdot 3 \cdot 2 \cdot 1$ , which equals $120$ .

Now, let's implement this using a recursive function:

# The function fact computes the factorial of the number n
def fact(n):
  if n == 0: return 1
  return n * fact(n-1)

# The main part of the program. Read the input value of n
n = int(input())

# Compute and print the answer
print(fact(n))

Now, let's understand how this recursive function works:

Base Case:

In our factorial function, the base case is when $n$ equals $0$ . In these cases, we know that the factorial of $0$ is always $1$ . So, we return $1$ .

Recursive Case:

For any other value of $n$ (when $n$ is greater than $1$ ), we compute the factorial recursively. We call the factorial function with the argument $n - 1$ and multiply the result by $n$ .
This means that to compute $f a c t (n)$ , we need to first compute $f a c t (n - 1)$ , then multiply the result by $n$ . This process continues until we reach the base case.

Let's walk through an example:

If we want to compute $f a c t (5)$ , the function will call $f a c t (4)$ , which will call $f a c t (3)$ , and so on, until we reach the base case.
Once we reach the base case $(f a c t (1))$ , we start "unwinding" the recursive calls.
Each recursive call returns its result and multiplies it by the current value of $n$ .
Finally, the result of $f a c t (5)$ is computed as $f a c t (4) \cdot 5$ , which is further computed as $f a c t (3) \cdot 4 \cdot 5$ , and so on, until we have the final result.

This is how recursion works! It’s like peeling layers of an onion — one layer at a time — until you reach the core. And understanding this recursive process is crucial for mastering recursive functions in programming.

Demonstrate how recursive functions work step by step, emphasizing the importance of the base case

Now let's walk through how recursive functions work step by step using the Fibonacci sequence as an example. The Fibonacci sequence is a series of numbers where each number is the sum of the two preceding ones, typically starting with $0$ and $1$ . So, the sequence goes: $0, 1, 1, 2, 3, 5, 8, 13$ , and so on.

The Fibonacci sequence has the following form:

The largest Fibonacci number that fits into the int type is

f_{46} = 1836311903

For $n \leq 40$ it's sufficient to use the int data type.

Let the function $f ib (n)$ compute the $n$ -th Fibonacci number. Then we have the following recurrence relation:

f ib (n) = ⎩ ⎨ ⎧ f ib (n - 1) + f ib (n - 2), n > 1 1, n = 1 0, n = 0

Now, let's implement a recursive function to compute the Fibonacci numbers:

# The function fib computes the n-th Fibonacci number
def fib(n):
  if (n == 0): return 0
  if (n == 1): return 1
  return fib(n - 1) + fib(n - 2)

# The main part of the program. Read the input value of n
n = int(input())

# Compute and print the answer
print(fib(n))

Now, let's break down how this recursive function works step by step:

Base Case:

The base cases are when $n$ is $0$ and $1$ . In these cases, we know the Fibonacci number directly: $F_{0} = 0$ and $F_{1} = 1$ . These are the simplest cases where we don't need further computation.

Recursive Case:

For any other value of $n$ (when $n > 1$ ), we compute the Fibonacci number recursively. We do this by adding the Fibonacci numbers of the two preceding positions in the sequence ( $f ib (n - 1)$ and $f ib (n - 2)$ ).
This means that to compute $f ib (n)$ , we need to first compute $f ib (n - 1)$ and $f ib (n - 2)$ , and then add their results together. This process continues until we reach the base cases.

Let's walk through an example:

If we want to compute $f ib (4)$ , the function will call $f ib (3)$ and $f ib (2)$ .
$f ib (3)$ will further call $f ib (2)$ and $f ib (1)$ , and $f ib (2)$ will call $f ib (1)$ and $f ib (0)$ .
$f ib (1)$ and $f ib (0)$ are base cases, so they return $1$ and $0$ , respectively.
Once we have the results of $f ib (1)$ and $f ib (0)$ , $f ib (2)$ will add them together $(0 + 1 = 1)$ .
$f ib (3)$ will similarly add the results of $f ib (2)$ and $f ib (1) (1 + 1 = 2)$ .
Finally, $f ib (4)$ will add $f ib (3)$ and $f ib (2) (2 + 1 = 3)$ , and we get the result $3$ .

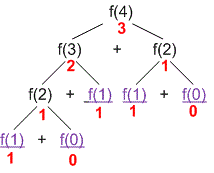
This step-by-step process demonstrates how recursive functions work, gradually breaking down the problem into smaller subproblems until reaching the base cases, and then combining the results to solve the original problem. And as we’ve seen, the base cases play a crucial role in stopping the recursion and providing the starting points for our computation.

Discuss the call stack and how it is used in recursive function calls

Now let's delve into the concept of the call stack and how it's used in recursive function calls. Imagine the call stack as a stack of plates in a cafeteria. When you enter the cafeteria, you pick up a plate and add it to the top of the stack. Similarly, when a function is called in a program, information about that function call is added to the call stack.

Let's see how this works with recursive function calls:

Function Calls and the Call Stack:

When a function is called, a new frame is created on top of the call stack to store information about that function call. This includes the function's parameters, local variables, and the return address — the point in the program where execution should continue after the function call.
Each time a new function is called (whether it's a recursive call or a regular function call), a new frame is added to the top of the call stack.

Recursive Function Calls:

In the case of recursive function calls, the function calls itself within its own body. This means that each recursive call creates a new frame on top of the call stack.
As the recursion progresses, more and more frames are added to the call stack, each representing a separate instance of the function call.
The call stack keeps track of all these function calls, ensuring that the program knows where to return to after each function call completes.

Base Case and Unwinding the Stack:

Eventually, as the recursion progresses, the base case is reached. This is the stopping condition that prevents the recursion from continuing indefinitely.
When the base case is reached, the function stops making further recursive calls and starts "unwinding" the call stack.
Each frame is popped off the call stack, and the program returns to the point where the function was originally called. This process continues until the entire call stack is unwound.

Memory Considerations:

It's important to note that the call stack has a limited size, and excessive recursion can lead to a stack overflow error if the stack becomes too deep.
Therefore, when writing recursive functions, it's crucial to ensure that there's a proper base case to prevent infinite recursion and to limit the depth of recursion to avoid stack overflow.

In summary, the call stack plays a crucial role in managing function calls, including recursive function calls. It keeps track of the sequence of function calls and ensures that the program knows where to return to after each function call completes. Understanding the call stack is essential for understanding how recursion works and for writing efficient and error-free recursive functions.

Clarify the concept of infinite recursion and how to avoid it

Now let's clarify the concept of infinite recursion and discuss how to avoid it.

Infinite Recursion:

Infinite recursion occurs when a recursive function calls itself indefinitely without reaching a base case that would stop the recursion.
In other words, the function keeps making recursive calls without making progress towards a base case, leading to an infinite loop of function calls.
This can quickly consume all available system resources and cause the program to crash or hang indefinitely.

How It Happens:

Infinite recursion typically occurs when there's a missing or incorrect base case in the recursive function.
Without a base case, or with a base case that's never reached due to incorrect logic, the function will keep calling itself forever.

Example:

Let's consider a simple example of a recursive function to count down from a given number:

def countDown(n):
  # Print current number
  print(n)
  # Call countDown function with the next smaller number
  countDown(n - 1)

# Example usage:
countDown(5)  # Prints numbers from 5 down to minus infinity

In this case, there's no base case to stop the recursion, so the function will keep calling itself with a smaller value of $n$ , leading to infinite recursion.

How to Avoid Infinite Recursion:

To avoid infinite recursion, it's crucial to ensure that every recursive function has a proper base case.
The base case should represent a condition under which the function stops making further recursive calls and returns a result.
When writing a recursive function, always ask yourself: "What condition should cause the function to stop and return a result?"
Make sure that the base case is reachable and that the recursive calls lead towards it.

Example Fixed:

Let's fix the previous example by adding a base case to stop the recursion when $n$ reaches $0$ :

def countDown(n):
  # Base case
  if n == 0: return
  # Print current number
  print(n)
  # Call countDown function with the next smaller number
  countDown(n - 1)

# Example usage:
countDown(5)  # Prints numbers from 5 down to 1

Now, the function will stop calling itself when $n$ becomes $0$ , preventing infinite recursion.

In summary, infinite recursion occurs when a recursive function calls itself indefinitely without reaching a base case. To avoid it, always ensure that your recursive functions have a proper base case that stops the recursion and returns a result. Testing your recursive functions with different input values can help catch potential cases of infinite recursion during development.

Implementing Recursive Algorithms

Present a series of programming problems suitable for recursion

Let's discuss some well-known recursive algorithms.

We can solve the problem using $O (n)$ complexity algorithm. We can write a just naive for loop:

# Read the input data
x, n, m = map(int,input().split())

# Initializes a variable res to 1.
# This variable will store the result of x^n mod m
res = 1

# compute the value x^n mod m using n multiplications 
# 1 * x * x * ... * x
for i in range(1,n+1):
  res = (res * x) % m

# print the answer
print(res)

This program exceeds Time Limit. Since $n \leq 1 0^{9}$ , and the time limit for this problem is just $1$ second, you can't perform $1 0^{9}$ operations in $1$ second even using modern computers.

How can we spped up the multiplication process? For example, if we want to compute $x^{100}$ , we can break it down into $(x^{2})^{50}$ . By using just one multiplication to compute $x^{2}$ , we can effectively decrease the power by half: from $100$ to $50$ .

For example, instead of using $16$ multiplications to find $x^{16}$ , we can rewrite the expression as follows: $x^{16} = (((x^{2})^{2})^{2})^{2}$ , thus performing only $4$ multiplications. Similarly, we can conclude that to find $x^{1024}$ , its enough to perform just $10$ multiplications.

If the exponent is odd, for example, $n = 99$ , we compute the value of $x^{99}$ as $x \cdot x^{98}$ .

For example, $x^{15} = ((x^{2} \cdot x)^{2} \cdot x)^{2} \cdot x$ .

We came to the binary exponentiation method, a technique used to compute large powers of a number efficiently. It's based on the principle that any number raised to a power can be expressed as a sequence of powers of $2$ .

Given a base $x$ and an exponent $n$ , we express $n$ as a sum of powers of $2$ . For example, if $n = 13$ , we can write it as $13 = 8 + 4 + 1$ . We then compute $x^{n}$ by multiplying together $x$ raised to each power of $2$ and combine the results.

Let's say we want to compute $x^{13}$ .

Express $13$ in binary: $13 = 1101$ in binary representation.
Then compute $x^{1}$ , $x^{4}$ and $x^{8}$ (corresponding to the set bits in the binary representation of $13$ ).
Finally, multiply these values together: $x^{13} = x^{1} \cdot x^{4} \cdot x^{8}$ .

Advantages. Binary exponentiation reduces the number of multiplications needed compared to naive exponentiation. It's particularly efficient for large exponents, as it requires only $O (l o g_{2} n)$ multiplications instead of $O (n)$ multiplications.

To find the value of $x^{n} m o d m$ , we shall use the formula:

x^{n} m o d m = ⎩ ⎨ ⎧ (x^{2})^{n /2} m o d m, i f n i s e v e n (x \cdot x^{n - 1}) m o d m, i f n i s o dd 1, n = 0

# The myPow function  finds the value of x^n mod m
def myPow(x, n, m):
  if (n == 0): return 1
  if (n % 2 == 0): return myPow((x * x) % m, n / 2, m)
  return (x * myPow(x, n - 1, m)) % m

# The main part of the program. Read the input data
x, n, m = map(int, input().split())

# Compute and print the answer
print(myPow(x, n, m))

Python has a built-in function $p o w (x, n, m)$ , which computes $x^{n} m o d m$ . The previous code can be rewritten as follows:

# Read the input data
x, n, m = map(int, input().split())

# Compute and print the answer
print(pow(x, n, m))

The Greatest Common Divisor (GCD) of two integers $a$ and $b$ is the largest positive integer that divides both $a$ and $b$ without leaving a remainder.

Example:

Let's take two integers, $a = 12$ and $b = 18$ .
The divisors of $12$ are $1, 2, 3, 4, 6$ , and $12$ .
The divisors of $18$ are $1, 2, 3, 6, 9$ , and $18$ .
The common divisors of $12$ and $18$ are $1, 2, 3$ , and $6$ .
Out of these common divisors, the largest one is $6$ .
Therefore, $g c d (12, 18) = 6$ .

Properties:

The GCD is always a positive integer.
If $a$ and $b$ are both zero, then $g c d (a, b) = 0$ .
If $a$ or $b$ (or both) is negative, then $g c d (a, b)$ is the same as the GCD of their absolute values.
If $a$ or $b$ is zero, then $g c d (a, b)$ is the absolute value of the non-zero integer.
The GCD of any number and $0$ is the absolute value of the number itself.

Applications:

GCD is used in various mathematical computations, including simplifying fractions and finding the least common denominator.
It's used in cryptographic algorithms, such as RSA, for key generation and encryption.
It's also used in computer science algorithms, such as the Euclidean algorithm for finding the GCD of two numbers efficiently.

The Euclidean algorithm is an efficient method for finding the GCD of two integers. It's based on the principle that the GCD of two numbers remains the same if we subtract the smaller number from the larger number until one of them becomes zero.

If instead of "minus" operation we'll use "mod" operation, calculations will go faster.

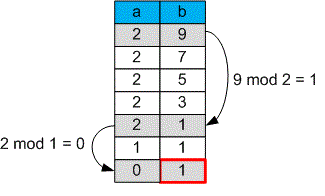
For example, to find the $GC D (1, 1 0^{9})$ using subtraction, $1 0^{9}$ operations should be performed. However, when using the modulo operation, only one action is sufficient.

Given two integers $a$ and $b$ , where $a \geq b$ , we repeatedly perform the following steps:

If $b$ is zero, the GCD is $a$ .
Otherwise, we replace $a$ with $b$ and $b$ with the remainder when $a$ is divided by $b$ . This can be expressed as $a \leftarrow b$ and $b \leftarrow a m o d b$ .
We continue this process until $b$ becomes zero.

The GCD of $a$ and $b$ is the value of $a$ when $b$ becomes zero.

The Euclidean algorithm is efficient, with a time complexity of $O (l o g_{2} min (a, b))$ . It's guaranteed to terminate since the value of $b$ decreases with each iteration, and eventually, $b$ becomes zero.

GCD of two numbers can be found using the formula:

GC D (a, b) = ⎩ ⎨ ⎧ a, b = 0 b, a = 0 GC D (a m o d b, b), a \geq b GC D (a, b m o d a), a < b

def gcd(a, b):
  if a == 0: return b
  if b == 0: return a
  if a > b: return gcd(a % b, b)
  return gcd(a, b % a)

# The main part of the program. Read the input data. 
a, b = map(int, input().split())

# Find and print the GCD of two numbers.
print(gcd(a, b))

The given formula can be expressed in another form:

GC D (a, b) = {a, b = 0 GC D (b, a m o d b), b \neq = 0

def gcd(a, b):
  if b == 0: return a
  return gcd(b, a % b)

# The main part of the program. Read the input data.
a, b = map(int, input().split())

# Find and print the GCD of two numbers.
print(gcd(a, b))

Python has a built-in function $g c d (a, b)$ that computes the Greatest Common Divisor of two numbers. The previous code can be rewritten as follows:

import math

#  Read the input data.
a, b = map(int, input().split())

# Find and print the GCD of two numbers.
print(math.gcd(a, b))

List of problems

Recursive programs:

Fibonacci numbers:

3258. Fibonacci sequence (used in lecture)
8295. Fibonacci string generation

GCD / LCM:

136. The segment
1601. GCD of two numbers (used in lecture)
1602. LCM of two integers
2214. Function 9
7363. Sum of fractions

Binomial coefficient:

3260. How many?

Exponentiation:

273. Modular exponentiation
5198. Modular exponentiation (used in lecture)
9644. Sum of powers
9646. Sum of powers 2

Comments

Nothing yet

Be the first one to start the conversation!

Loading

Just a moment, getting data from the server