Editorial

Let $i\cdot j(i\le j)$ represent the dimensions of a rectangle that can be formed using the squares. Given that $i\le j$ and $i\cdot j\le n$, it follows that $i\le \sqrt{n}$.

Let's iterate over the smaller side of the rectangle $i$ from $1$ to $\sqrt{n}$. For each $i$, iterate over the second side $j$, from $i$ until $i\cdot j\le n$. In the variable $cnt$, count the number of such pairs $(i,j)$.

    cnt = 0;
    for (i = 1; i <= sqrt(n); i++)
    for (j = i; i * j <= n; j++) 
      cnt++;

The second loop can be replaced with a formula. Notice that $j$ in the loop runs from $i$ to $n/i$. Therefore, during the $i$-th iteration, the value of $cnt$ increases by $n/i-i+1$. The double loop can thus be rewritten as follows:

cnt = 0;
for (i = 1; i <= sqrt(n); i++)
  cnt = cnt + (n / i - i + 1);

Example

Consider the first test case where $n=6$. The smaller side of the rectangle iterates from $1$ to $\lfloor \sqrt{6}\rfloor =2$.

For $i=1$, the second side $j$ can take values from $i=1$ to $n/i=6$. This gives us $6$ rectangles:

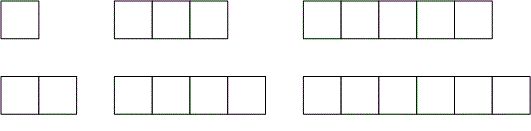
For $i=2$, the second side $j$ can take values from $i=2$ to $n/i=3$. This gives us $2$ rectangles:

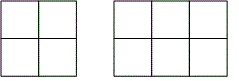
In total, for $n=6$, there are $8$ possible rectangles.

Algorithm realization

Read the input value of $n$.

scanf("%d", &n);

Compute the answer.

cnt = 0;
for (i = 1; i <= sqrt(n); i++)
  cnt = cnt + (n / i – i + 1);

Print the answer.

printf("%lld\n", cnt);

Python realization

import math

Read the input value of $n$.

n = int(input())

Compute the answer.

cnt = 0
for i in range(1, int(math.sqrt(n)) + 1):
  cnt += (n // i - i + 1)

Print the answer.

print(cnt)