Editorial

Note that if the numbers $n$ and $n-3$ are placed in one group, and $n-1$ and $n-2$ are placed in the other (so that the sum of numbers in each group is equal), the problem reduces to a similar problem of smaller size, namely, dividing the numbers $1,2,...,n-4$ into two groups.

For $n\le 3$, the numbers are divided into groups as follows:

• If three numbers $1,2,3$ remain, they can be divided into two groups: $\{1,2\}$ and $\{3\}$.

• If two numbers $1,2$ remain, they can be divided into groups: $\{1\}$ и $\{2\}$. The difference between the sums of the groups will be $1$.

• If one number $1$ remains, it can be placed in either group. The difference between the sums of the groups will be $1$.

If the sum of all numbers from $1$ to $n$ is even, they can be divided into two groups with equal sums.

If the sum of all numbers from $1$ to $n$ is odd, they can be divided into two groups with a sum difference of $1$.

Example

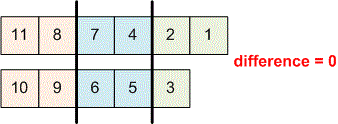
Let $n=10$. The numbers are placed into groups as follows:

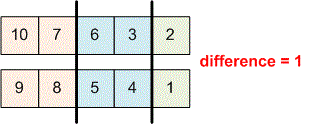
Let $n=11$. The numbers are placed into groups as follows:

Algorithm realization

Read the input value $n$.

scanf("%d", &n);

Initialize the initial sums of the numbers in the groups, $s_1$ and $s_2$ to $0$.

s1 = s2 = 0;

Iterate through the numbers from $n$ down to $1$.

for (i = n; i > 0; i--)

If $s_1<s_2$, place the number $i$ into the first group. Otherwise, place the number $i$ into the second group.

  if (s1 < s2)
  {
    s1 += i;
    a.push_back(i);
  }
  else
  {
    s2 += i;
    b.push_back(i);
  }

Print the sizes of the groups.

printf("%d %d\n", a.size(), b.size());

Print the numbers of the first group.

for (i = 0; i < a.size(); i++)
  printf("%d ", a[i]);
printf("\n");

Print the numbers of the second group.

for (i = 0; i < b.size(); i++)
  printf("%d ", b[i]);
printf("\n");