Editorial

Let the array $v$ store the identification numbers of the songs. Using two pointers, we will maintain a sliding window $[i;j]$ in which the songs do not repeat. In other words, all the songs in the segment $[i;j]$ are unique. The songs from this segment will be stored in a set $s$. For each value of $i$, we will try to extend the segment to the maximum possible length. That is, for a fixed $i$, we will search for such a $j$ that in the segment $[i;j]$ the songs do not repeat, but in the segment $[i;j+1]$ duplicates already appear.

When processing the current song at index $j+1$, there are two possible cases:

• If the song $v_{j+1}$ is not present in the segment $[i;j]$, add it to this segment, extending it to $[i;j+1]$;

• If the song $v_{j+1}$ is already present in the segment, shift the left boundary $i$ to the right until $v_{j+1}$ disappears from the segment $[i;j]$. Then, add $v_{j+1}$ to the segment, extending it to $[i;j+1]$. With each shift of $i$, remove the corresponding elements from the set $s$;

Among all possible segments $[i;j]$ with unique songs, find the maximum length. This will be the answer to the problem.

Example

Let’s consider how the segments with unique songs will change for the first example.

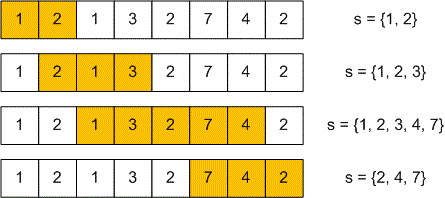
The length of the longest segment is $5$.

Algorithm realization

Read the input data. The identification numbers of the songs are stored in the array $v$.

scanf("%d", &n);
v.resize(n);
for (i = 0; i < n; i++)
  scanf("%d", &v[i]);

Maintain the segment $[i;j-1]$ of unique songs (i.e., the songs from $v_i$ to $v_{j-1}$ do not repeat). In the set $s$, store the identification numbers of the songs from this segment. The variable $res$ tracks the length of the longest fragment with unique songs.

i = res = 0;
for (j = 0; j < n; j++)
{

Consider the current song at index $j$. If it is already in the set $s$, it will not be possible to extend the current segment $[i;j-1]$ by including the $j$-th song. In this case, we need to shift the left boundary $i$, removing the song $v_i$ from the set $s$, until the $j$-th song disappears from the set $s$.

  while (s.find(v[j]) != s.end())
  {
    s.erase(v[i]);
    i++;
  }

Add the $j$-th song to the segment and, accordingly, to the set $s$. Thus, the segment $[i;j]$ will not contain any repeated songs.

  s.insert(v[j]);

Among all possible segments $[i;j]$, find the longest one. The length of the segment $[i;j]$ is $j-i+1$.

  res = max(res, j - i + 1);
}

Print the answer.

printf("%d\n", res);