Editorial

In this problem, your task is to find the shortest distance between two vertices in a directed weighted graph. To solve it, you need to implement Dijkstra's algorithm.

Example

The graph given in the example looks like this:

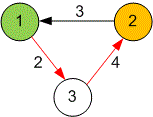
The shortest distance from vertex $1$ to vertex $2$ is $2+4=6$.

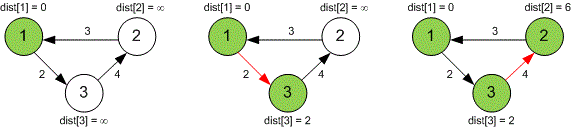
Algorithm implementation

Let's declare the constants and arrays we’ll use.

#define MAX 110
#define INF 0x3F3F3F3F
int m[MAX][MAX], used[MAX], d[MAX];

Read the input data.

scanf("%d %d %d", &n, &s, &f);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
{
  scanf("%d", &m[i][j]);
  if (m[i][j] == -1) m[i][j] = INF;
}

Initialize the arrays.

memset(used, 0, sizeof(used));
memset(d, 0x3F, sizeof(d));
d[s] = 0;

Start the loop for Dijkstra's algorithm. Since the graph contains $n$ vertices, $n-1$ iterations will be sufficient.

for (i = 1; i < n; i++)
{

Find the vertex with the smallest value of $d[j]$ among those for which the shortest distance from the source is not calculated (i.e., for which $used[j]=0$). Let this vertex be $w$.

  mind = INF;
  for (j = 1; j <= n; j++)
    if (used[j] == 0 && d[j] < mind) { mind = d[j]; w = j; }

If it is impossible to find a vertex to include in the set of vertices for which the shortest distance is already calculated, terminate the algorithm.

  if (mind == INF) break;

Relax all the edges outgoing from vertex $w$.

  for (j = 1; j <= n; j++)
    if (used[j] == 0) d[j] = min(d[j], d[w] + m[w][j]);

Mark that the shortest distance to $w$ is calculated (it is stored in $d[w]$).

  used[w] = 1;
}

Print the answer — the value of $d[f]$. If it is equal to infinity, then there is no path to vertex $f$.

if (d[f] == INF) d[f] = -1;
printf("%d\n", d[f]);

Python implementation

Let's declare the constants we'll use.

MAX = 110
INF = float('inf') / 2

Read the input data.

n, s, f = map(int, input().split())

m = [[0] * (n + 1)]
for _ in range(n):
  row = list(map(int, input().split()))
  m.append([0] + [INF if x == -1 else x for x in row])

Initialize the lists.

used = [False] * (n + 1)
d = [INF] * (n + 1)
d[s] = 0

Start the loop for Dijkstra's algorithm. Since the graph contains $n$ vertices, $n-1$ iterations will be sufficient.

for _ in range(n - 1):

Find the vertex with the smallest value of $d[j]$ among those for which the shortest distance from the source is not calculated (i.e., for which $used[j]=0$). Let this vertex be $w$.

  mind = INF
  w = -1
  for j in range(1, n + 1):
    if not used[j] and d[j] < mind:
      mind = d[j]
      w = j

If it is impossible to find a vertex to include in the set of vertices for which the shortest distance is already calculated, terminate the algorithm.

  if mind == INF:
    break

Relax all the edges outgoing from vertex $w$.

  for j in range(1, n + 1):
    if not used[j]:
      d[j] = min(d[j], d[w] + m[w][j])

Mark that the shortest distance to $w$ is calculated (it is stored in $d[w]$).

  used[w] = True

Print the answer — the value of $d[f]$. If it is equal to infinity, then there is no path to vertex $f$.

print(-1 if d[f] == INF else d[f])