Editorial

Find the shortest path in the graph from vertex $s$ to vertex $f$ using breadth first search.

Example

The graph given in the example, has the following form:

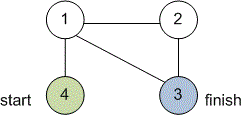
Algorithm realization

Declare an adjacency matrix $g$ to store the graph and an array $d i s t$ to store the shortest distances from the source to the vertices.

#define MAX 101
int g[MAX][MAX], dist[MAX];

The bfs function implements a breadth-first search starting from the vertex $s t a r t$ .

void bfs(int start)
{

Initialize the $d i s t$ array. If $d i s t [i] = - 1$ , it means that vertex $i$ is not visited.

  memset(dist, -1, sizeof(dist));
  dist[start] = 0;

Dclare and initialize a queue $q$ .

  queue<int> q;
  q.push(start);

Continue the breadth-first search as long as the queue is not empty.

  while (!q.empty())
  {

Extract and remove vertex $v$ from the front of the queue.

    int v = q.front(); q.pop();

Where can we go from vertex $v$ ? Iterate over the edges $v \to t o$ .

    for (int to = 1; to <= n; to++)

If there is an edge from $v$ to $t o$ and vertex $t o$ is not visited, then move to it (the edge $(v, t o)$ becomes an edge of the breadth-first search tree).

      if (g[v][to] && dist[to] == -1)
      {

Add vertex $t o$ to the end of the queue and compute the shortest distance $d i s t [t o]$ .

        q.push(to);
        dist[to] = dist[v] + 1;
      }
  }
}

The main part of the program. Read the input data.

scanf("%d %d %d", &n, &s, &f);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
  scanf("%d", &g[i][j]);

Start the breadth-first search from vertex $s$ .

bfs(s);

Print the shortest distance. If there is no path to vertex $f (d i s t [f] < 0)$ , set $d i s t [f] = 0$ .

if (dist[f] < 0) dist[f] = 0;
printf("%d\n", dist[f]);

Algorithm realization — adjacency list

Declare an adjacency list $g$ to store the graph and an array $d i s t$ to store the shortest distances from the source to the vertices.

vector<vector<int> > g;
vector<int> dist;

The bfs function implements a breadth-first search starting from the vertex $s t a r t$ .

void bfs(int start)
{

Initialize the $d i s t$ array. If $d i s t [i] = - 1$ , it means that vertex $i$ is not visited.

  dist = vector<int>(n + 1, -1);
  dist[start] = 0;

Dclare and initialize a queue $q$ .

  queue<int> q;
  q.push(start);

Continue the breadth-first search as long as the queue is not empty.

  while (!q.empty())
  {

Extract and remove vertex $v$ from the front of the queue.

    int v = q.front(); q.pop();

Where can we go from vertex $v$ ? Iterate over the edges $v \to t o$ .

    for (int to : g[v])

If vertex $t o$ is not visited, then move to it (the edge $(v, t o)$ becomes an edge of the breadth-first search tree).

      if (dist[to] == -1)
      {

Add vertex $t o$ to the end of the queue and compute the shortest distance $d i s t [t o]$ .

        q.push(to);
        dist[to] = dist[v] + 1;
      }
  }
}

The main part of the program. Read the input data.

scanf("%d %d %d", &n, &s, &f);
g.resize(n + 1);
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
{
  scanf("%d", &val);
  if (val == 1) g[i].push_back(j);
}

Start the breadth-first search from vertex $s$ .

bfs(s);

Print the shortest distance. If there is no path to vertex $f (d i s t [f] < 0)$ , set $d i s t [f] = 0$ .

if (dist[f] < 0) dist[f] = 0;
printf("%d\n", dist[f]);

Java realization — adjacency matrix

import java.util.*;

public class Main
{
  static int g[][], dist[];
  static int n, s, f;
    
  static void bfs(int start)
  {
    Arrays.fill(dist,-1);
    dist[start] = 0;

    Queue<Integer> q = new LinkedList<Integer>();
    q.add(start);

    while(!q.isEmpty())
    {
      int v = q.poll();
      for(int to = 1; to <= n; to++)
        if (g[v][to] == 1 && dist[to] == -1)
        {
          q.add(to);
          dist[to] = dist[v] + 1;
        }
    }
  }
  
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    n = con.nextInt();
    s = con.nextInt();
    f = con.nextInt();
    g = new int[n+1][n+1];
    dist = new int[n+1];
 
    for (int i = 1; i <= n; i++)
    for (int j = 1; j <= n; j++)    	
      g[i][j] = con.nextInt();
    
    bfs(s);

    if (dist[f] < 0) dist[f] = 0;
    System.out.println(dist[f]);
    
    con.close();
  }
}

Java realization — adjacency list

import java.util.*;

public class Main
{
  static ArrayList<Integer>[] g;	
  static int dist[];
  
  static void bfs(int start)
  {
    Arrays.fill(dist,-1);
    dist[start] = 0;

    Queue<Integer> q = new LinkedList<Integer>();
    q.add(start);

    while(!q.isEmpty())
    {
      int v = q.poll();
      for(int i = 0; i < g[v].size(); i++)
      {
        int to = g[v].get(i);
        if (dist[to] == -1)
        {
          q.add(to);
          dist[to] = dist[v] + 1;
        }
      }
    }
  }
  
  @SuppressWarnings("unchecked")  
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    int n = con.nextInt();
    int s = con.nextInt();
    int f = con.nextInt();
    
    g = new ArrayList[n+1];
    for(int i = 0; i <= n; i++)
      g[i] = new ArrayList<Integer>();
    
    dist = new int[n+1];

    for (int i = 1; i <= n; i++)
    for (int j = 1; j <= n; j++)
    {
      int val = con.nextInt();
      if (val == 1) g[i].add(j);
    }

    bfs(s);

    if (dist[f] < 0) dist[f] = 0;
    System.out.println(dist[f]);
    con.close();
  }
}

Python realization — adjacency matrix

Import the deque.

from collections import deque

The bfs function implements a breadth-first search starting from the vertex $s t a r t$ .

def bfs(start):

Initialize the $d i s t$ list. If $d i s t [i] = - 1$ , it means that vertex $i$ is not visited.

  global dist
  dist = [-1] * (n + 1)
  dist[start] = 0

Declare and initialize a queue $q$ .

  q = deque([start])

Continue the breadth-first search as long as the queue is not empty.

  while q:

Extract and remove vertex $v$ from the front of the queue.

    v = q.popleft()

Where can we go from vertex $v$ ? Iterate over the edges $v \to t o$ .

    for to in range(1, n + 1):

If there is an edge from $v$ to $t o$ and vertex $t o$ is not visited, then move to it (the edge $(v, t o)$ becomes an edge of the breadth-first search tree).

      if g[v][to] == 1 and dist[to] == -1:

Add vertex $t o$ to the end of the queue and compute the shortest distance $d i s t [t o]$ .

        q.append(to)
        dist[to] = dist[v] + 1

The main part of the program. Read the input data.

n, s, f = map(int, input().split())
g = [[] for _ in range(n + 1)]
for i in range(1, n + 1):
  g[i] = [0] + list(map(int, input().split()))

Start the breadth-first search from vertex $s$ .

bfs(s)

Print the shortest distance. If there is no path to vertex $f (d i s t [f] < 0)$ , set $d i s t [f] = 0$ .

if dist[f] < 0: dist[f] = 0
print(dist[f])

Python realization — adjacency list

Import the deque.

from collections import deque

The bfs function implements a breadth-first search starting from the vertex $s t a r t$ .

def bfs(start):

Initialize the $d i s t$ list. If $d i s t [i] = - 1$ , it means that vertex $i$ is not visited.

  global dist
  dist = [-1] * (n + 1)
  dist[start] = 0

Declare and initialize a queue $q$ .

  q = deque([start])

Continue the breadth-first search as long as the queue is not empty.

  while q:

Extract and remove vertex $v$ from the front of the queue.

    v = q.popleft()

Where can we go from vertex $v$ ? Iterate over the edges $v \to t o$ .

    for to in g[v]:

If vertex $t o$ is not visited, then move to it (the edge $(v, t o)$ becomes an edge of the breadth-first search tree).

      if dist[to] == -1:

Add vertex $t o$ to the end of the queue and compute the shortest distance $d i s t [t o]$ .

        q.append(to)
        dist[to] = dist[v] + 1

The main part of the program. Read the input data.

n, s, f = map(int, input().split())

Initialize and construct the adjacency list $g$ .

g = [[] for _ in range(n + 1)]
for i in range(1, n + 1):
  row = [0] + list(map(int, input().split()))
  for j in range(1, n + 1):
    if row[j] == 1: g[i].append(j)

Start the breadth-first search from vertex $s$ .

bfs(s)

Print the shortest distance. If there is no path to vertex $f (d i s t [f] < 0)$ , set $d i s t [f] = 0$ .

if dist[f] < 0: dist[f] = 0
print(dist[f])