Algorithm Analysis

Let's denote by $f(n)$ the number of sought sequences of 0s and 1s of length $n$. If the first position of the sequence contains a 0, then starting from the second position, one can construct $f(n-1)$ sequences. If the first position contains a 1, then both variants are possible for the second position. If there is a 0, then on the next $n-2$ free positions, one can construct $f(n-2)$ sequences. If there is a 1, then a 0 must be present at the third position, and starting from the fourth position, one can construct $f(n-3)$ sequences.

We have the recurrence relation: $f(n)=f(n-1)+f(n-2)+f(n-3)$. It remains to compute the initial values:

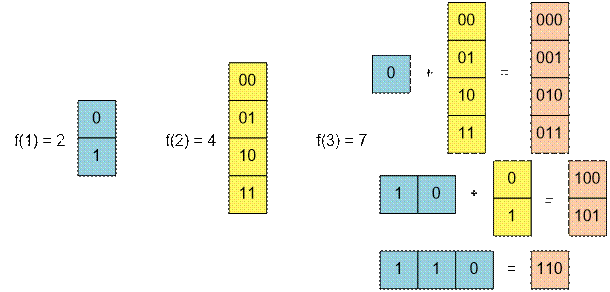
• $f(1)=2$, since there are two sequences of length 1: 0 and 1.

• $f(2)=4$, since there are four sequences of length 2: 00, 01, 10, and 11.

• $f(3)=7$, since there are seven sequences of length 3: 000, 001, 010, 011, 100, 101, and 110.

Example

Algorithm Implementation

Declare an array f, in which we will store the values f(1), f(2), …, f(n).

int f[100010];

Read the input value n.

scanf("%d",&n);

Store in the respective cells of the array f the values f(1), f(2), and f(3).

f[1] = 2; f[2] = 4; f[3] = 7;

Compute the value of f(i) using the recurrence formula. Perform the computation modulo 12345.

for(i = 4; i <= n; i++)
    f[i] = (f[i-1] + f[i-2] + f[i-3]) % 12345;

Output the answer.

printf("%d\n",f[n]);

Algorithm Implementation – Recursion + Memoization

Declare an array dp for memoizing the results: dp[i] will store the value f(i).

int dp[100001];

Implement the function f(n) – the number of sought sequences of 0s and 1s of length n. Use the memoization technique.

int f(int n)
{
    if (n == 1) return 2;
    if (n == 2) return 4;
    if (n == 3) return 7;
    if (dp[n] != -1) return dp[n];
    return dp[n] = (f(n-1) + f(n-2) + f(n-3)) % 12345;
}

The main part of the program. Read the input value n.

scanf("%d",&n);

Initialize the array dp.

memset(dp,-1,sizeof(dp));

Compute and output the value f(n).

printf("%d\n",f(n));

Java Implementation

import java.util.*;

public class Main
{
    public static int MAX = 100010;
    static int f[] = new int[MAX];

    public static void main(String[] args)
    {
        Scanner con = new Scanner(System.in);
        int n = con.nextInt();
        f[1] = 2; f[2] = 4; f[3] = 7;
        for(int i = 4; i <= n; i++)
            f[i] = (f[i-1] + f[i-2] + f[i-3]) % 12345;
        System.out.println(f[n]);
        con.close();
    }
}

Python Implementation

n = int(input())

dp = [0] * (n + 4)
dp[1], dp[2], dp[3] = 2, 4, 7

for i in range(4, n + 1):
    dp[i] = (dp[i-1] + dp[i-2] + dp[i-3]) % 12345;

print(dp[n])

Python Implementation – Recursion with Memoization

Increase the stack size for recursion.

import sys
sys.setrecursionlimit(10000)

def f(n):
    if n == 1: return 2
    if n == 2: return 4
    if n == 3: return 7
    if dp[n] != -1: return dp[n]

    dp[n] = (f(n - 1) + f(n - 2) + f(n - 3)) % 12345
    return dp[n]

n = int(input())

dp = [-1] * 100001

print(f(n))