Исследуя рекурсию

Цель этого урока — познакомить студентов с понятием рекурсии, понять ее основы и овладеть ее реализацией в программировании. К концу этого урока студенты должны быть способны:

• Дать определение рекурсии и описать ее основные характеристики.

• Разобраться в механизме работы рекурсивных функций.

• Реализовать базовые рекурсивные алгоритмы.

• Идентифицировать ситуации, в которых рекурсия является подходящим решением.

Вступление:

• Начните с краткого обсуждения методов решения задач в программировании.

• Приведите пример рекурсии из реальной жизни.

• Определите рекурсию как технику программирования, при которой функция вызывает саму себя напрямую или косвенно для решения задачи.

• Поясните ключевые характеристики рекурсии: базис, рекурсивный шаг и вызов самой себя.

Понимание рекурсивных функций:

• Объясните механизм работы рекурсивных функций, используя простой пример (факториал, вычисление степени $x^n$ или последовательность Фибоначчи).

• Продемонстрируйте работу рекурсивных функций шаг за шагом, подчёркивая важность базового случая.

• Обсудите стек вызовов и его использование при рекурсивных вызовах функций.

• Поясните концепцию бесконечной рекурсии и способы ее избегания.

Реализация рекурсивных алгоритмов:

• Представьте серию задач по программированию, подходящих для решения с помощью рекурсии.

• Разделите студентов на пары или небольшие группы для решения этих задач рекурсивным способом.

• Поощряйте студентов писать рекурсивные функции с нуля, уделяя особое внимание определению базового и рекурсивного случаев.

• Следите за работой групп, чтобы при необходимости предоставлять им помощь и помогать советами.

Обзор и практика:

• Пусть каждая группа представит свои рекурсивные решения классу.

• Обсудите оптимальность и воспринимаемость различных рекурсивных подходов.

• Разберите общие трудности и заблуждения, с которыми столкнулись участники во время выполнения задания.

• Предоставьте дополнительные задачи для практики, чтобы студенты могли работать над ними индивидуально или в группах.

Заключение:

• Подведите итоги основных моментов, рассмотренных на уроке, подчеркнув силу и универсальность рекурсии в программировании.

• Поощряйте студентов продолжать изучать рекурсию в своих проектах и заданиях.

Домашнее задание:

• Дайте домашнее задание для закрепления изученных в классе понятий. Например, реализовать рекурсивные алгоритмы для конкретных задач или проанализировать существующие рекурсивные функции в библиотеках кода.

Оценивание:

• Оцените понимание студентов через их участие в обсуждениях на семинарах, способности решать рекурсивные задачи по программированию и умению чётко объяснять рекурсивные решения.

• Проверьте домашние задания, чтобы оценить индивидуальное освоение концепций рекурсии и навыков их реализации.

Вступление

Начнем с краткого обсуждения методов решения задач в программировании

В программировании решение задач является фундаментальным навыком, который Вы будете использовать каждый раз, когда будете писать код. Прежде чем мы углубимся в особенности рекурсии, давайте поговорим о методах решения задач.

Думайте о решении задач как о путешествии. Вы начинаете с задачи, программу для которой следует написать. И Вам нужно понять, как перейти от точки $А$ (условию) к точке $В$ (решению). Это путешествие включает в себя разбиение задачи на более мелкие части, с которыми удобнее работать, понимание правил или ограничений, а также разработку плана достижения желаемого результата.

Существует несколько техник, которые программисты используют для эффективного решения задач. Вот некоторые из них:

• Понимание задачи: прежде чем Вы начнете решать задачу, Вам необходимо полностью понять её. Это включает в себя чтение и анализ ее условия, определение входных и выходных данных, а также разъяснение любых неясностей.

• Разделяй и властвуй: многие сложные задачи можно решить, разбив их на более мелкие, более простые подзадачи. Этот подход, известный как "разделяй и властвуй", позволяет Вам решать каждую подзадачу отдельно, а затем комбинировать решения, чтобы решить более крупную.

• Алгоритмическое мышление: Алгоритмы — это пошаговые процедуры для решения задач. Когда Вы сталкиваетесь с задачей, попытайтесь мыслить алгоритмически, разбивая решение на последовательность логических шагов.

• Абстракция: Абстракция предполагает сосредоточение на существенных деталях задачи, игнорируя несущественную или отвлекающую информацию. Абстрагируя ненужные детали, Вы сможете упростить задачу и сосредоточиться на важном.

• Итерация и рекурсия: Итерация предполагает решение задачи через многократное выполнение цикла или последовательности команд. Рекурсия, с другой стороны, предполагает решение задачи путем её разбиения на меньшие экземпляры той же самой задачи. Как итерация, так и рекурсия являются мощными методами решения задач, с которыми Вы часто будете сталкиваться в программировании.

Овладев указанными методами решения задач, Вы будете лучше подготовлены к решению широкого спектра задач по программированию, включая те, которые связаны с рекурсией. Поэтому, углубляясь в изучение рекурсии, помните об этих стратегиях решения задач — они станут ценными инструментами в Вашем арсенале программирования.

Приведите концепцию рекурсии на примере из реальной жизни

Давайте на мгновение отойдем от программирования и подумаем о рекурсии на примерах из реальной жизни. Представьте, что Вы стоите перед набором русских матрешек. Эти куклы бывают разных размеров, и каждая помещается внутри следующей, большей по размеру.

Теперь давайте подумаем, как Вы могли бы описать процесс открытия каждой матрешки в наборе. Начинаете Вы с самой большой, и когда ее открываете, то находите внутри меньшую матрешку. Затем Вы открываете эту меньшую матрешку и обнаруживаете внутри еще меньшую, и так далее, пока не достигнете самой маленькой — той, которая не содержит внутри себя других матрешек.

Процесс открытия каждой матрешки можно считать рекурсивным. Почему? Потому что каждая матрешка имеет схожую структуру с другими, и действие по её открытию одинаково для каждой – оно включает в себя взгляд внутрь, чтобы увидеть, есть ли там меньшая матрешка.

В терминах программирования рекурсия работает аналогичным образом. Вместо открытия русских матрешек мы "открываем" функции или методы. Рекурсивная функция — это функция, которая вызывает саму себя, либо напрямую, либо косвенно, чтобы решить задачу, разбивая её на более мелкие экземпляры той же самой задачи.

Как и с матрешками, рекурсия решает задачу путем её разбиения на меньшие, подобные подзадачи, до тех пор, пока мы не достигнем точки, где задача становится настолько маленькой и простой, что мы можем решить её напрямую. Эта самая маленькая и простая версия задачи называется базовым случаем.

Понимая рекурсию через примеры из реальной жизни, такие как русские матрешки, мы видим, как она применяется в программировании, и насколько она может быть мощным инструментом для решения сложных задач. Поэтому, углубляясь в изучение рекурсии, держите эту визуальную аналогию в уме — она поможет Вам интуитивно понять концепцию.

Определите рекурсию как метод программирования, при котором функция вызывает саму себя напрямую или косвенно для решения задачи

Теперь давайте упростим определение рекурсии. Представьте, что у Вас есть функция — набор инструкций, выполняющих определенную задачу в Вашей программе. А теперь представьте, что эта функция может вызывать саму себя. Да, вы не ослышались! Это и называется рекурсией.

Рекурсия похожа на цикл, но вместо того чтобы повторять набор инструкций до тех пор, пока не будет выполнено условие, рекурсивная функция повторяет саму себя, вызывая саму себя – напрямую или косвенно — до тех пор, пока не достигнет определенного условия, обычно называемого базовым случаем.

Позвольте объяснить это на примере. Представьте, что у Вас есть функция "countDown", которая выводит числа от $n$ до $1$. Вместо использования цикла мы можем определить "countDown" рекурсивно. Вот как это работает:

• На вход функции "countDown" подается число $n$.

• Если число равно $1$ (базовый случай), то функция выводит "$1$" и завершается.

• Если число больше $1$, то функция выводит текущее число, а затем вызывает саму себя с меньшим следующим числом.

• Этот процесс продолжается до тех пор, пока функция не достигнет базового случая, после чего она перестает вызывать саму себя, и рекурсия "разворачивается" обратно к исходному вызову.

def countDown(n):
  # Базовый случай: если n = 1, то выводим его и останавливаем рекурсию
  if n == 1:
    print(n)
  else:
    # Выводим текущее число
    print(n)
    # Вызываем функцию countDown со следующим меньшим числом
    countDown(n - 1)

# Пример вызова:
countDown(5)  # Вывести числа от 5 до 1 по убыванию

Таким образом, рекурсия — это способ решения задач путем разбиения их на более маленькие, подобные подзадачи, а затем решения этих подзадач путем многократного вызова одной и той же функции, пока мы не достигнем базового случая, где задачу можно решить напрямую.

Имейте в виду, что рекурсия может быть немного запутанной сначала, но с практикой и пониманием её принципов Вы сможете использовать её как мощный инструмент в своих уроках по программированию.

Выделите ключевые характеристики рекурсии: базис, рекурсивный шаг и вызов самой себя

Теперь, когда мы понимаем, что такое рекурсия и как она работает, давайте углубимся в её ключевые характеристики. Рекурсия подобна хорошо отлаженному механизму – у неё есть определённые части, которые работают вместе, чтобы обеспечить её функционирование. Вот три ключевые характеристики рекурсии, на которых мы остановимся: базис, рекурсивный вызов и вызов самой себя.

Базис:

• Представьте базис рекурсии как точку остановки для рекурсивной функции. Это условие, которое указывает функции, когда прекратить вызывать саму себя и начинать возвращать значения.

• Без базиса рекурсивная функция продолжала бы вызывать саму себя бесконечно, что привело бы к так называемой бесконечной рекурсии, чего мы не желаем.

• В предыдущем примере с функцией “countDown” базовым был случай, когда $n$ становилось равным $1$. В этот момент мы просто выводили $1$ и прекращали вызов функции.

Шаг рекурсии:

• Рекурсивный шаг есть то место, где происходит магия рекурсии. Это часть функции, в которой мы вызываем саму функцию.

• Каждый раз, когда функция производит рекурсивный вызов, мы на шаг становимся ближе к базовому случаю. Мы разбиваем задачу на всё меньшие и меньшие подзадачи, пока не достигнем базового случая.

• В функции "countDown" рекурсивный шаг выполняется когда $n$ больше $1$. Мы выводим текущее значение $n$, а затем снова вызываем функцию "countDown" с аргументом $n–1$.

Вызов самой себя:

• Эта характеристика может звучать сложно, но на самом деле она довольно проста. Самовызов означает, что функция вызывает саму себя.

• Когда мы определяем рекурсивную функцию, мы по сути говорим: "Эй, функция, ты можешь вызвать саму себя, если это необходимо".

• Природа самовызова позволяет рекурсии решать сложные задачи, разбивая их на более мелкие экземпляры той же задачи.

• В функции "countDown" мы видели самовызов в действии, когда вызывали "countDown" внутри самой функции.

Итак, подведем итог. Рекурсия имеет три ключевые характеристики:

1. базовый случай, который описывает нам когда остановиться;

2. шаг рекурсии, который разбивает задачу на более мелкие подзадачи;

3. самовызов, который позволяет функции вызывать саму себя.

Понимание и освоение этих характеристик необходимо для того, чтобы понимать рекурсию и эффективно использовать её в программировании.

Понимание рекурсивных функций

Пояснение механизма рекурсивных функций на примере

Давайте разберем механизм рекурсивных функций на примере вычисления факториала числа.

Факториал неотрицательного целого числа $n$, обозначаемый как $n!$, является произведением всех положительных целых чисел, меньших или равных $n$. Например, $5!$ (читается как "пять факториал") равен $5\cdot 4\cdot 3\cdot 2\cdot 1$, что равно $120$.

Теперь давайте реализуем это с помощью рекурсивной функции:

# Функция fact вычисляет факториал числа n
def fact(n):
  if n == 0: return 1
  return n * fact(n-1)

# Основная часть программы. Читаем входное значение n
n = int(input())

# Вычисляем и выводим ответ
print(fact(n))

Теперь давайте поймем, как работает эта рекурсивная функция:

Базовый случай:

• В функции вычисления факториала базовый случай — это когда значение $n$ равно $0$. Мы знаем, что факториал $0$ равен $1$. Поэтому мы возвращаем $1$.

Шаг рекурсии:

• Для любого другого значения $n$ (когда $n$ больше $1$) мы вычисляем факториал рекурсивно. Мы вызываем функцию факториала с аргументом $n-1$ и умножаем результат на $n$.

• Это означает, что для вычисления $fact(n)$ нам сначала нужно вычислить $fact(n-1)$, а затем умножить результат на $n$. Этот процесс продолжается до тех пор, пока мы не достигнем базового случая.

Давайте рассмотрим пример.

• Если мы хотим вычислить $fact(5)$, то функция вызовет $fact(4)$, которая вызовет $fact(3)$, и так далее, пока мы не достигнем базового случая.

• Когда мы достигнем базового случая $(fact(1))$, то начнем "разматывать" рекурсивные вызовы.

• Каждый рекурсивный вызов возвращает свой результат и умножает его на текущее значение $n$.

• В итоге результат $fact(5)$ вычисляется как $fact(4)\cdot 5$, который далее вычисляется как $fact(3)\cdot 4\cdot 5$ и так далее, пока мы не получим окончательный результат.

Вот как работает рекурсия! Это похоже на снятие слоев с луковицы — слой за слоем — пока не доберешься до сердцевины. Понимание этого рекурсивного процесса необходимо для освоения рекурсивных функций в программировании.

Продемонстрируйте пошаговую работу рекурсивных функций, подчеркивая важность базового случая

Теперь давайте поэтапно рассмотрим, как работают рекурсивные функции, используя последовательность Фибоначчи в качестве примера. Последовательность Фибоначчи — это ряд чисел, в котором каждое число является суммой двух предыдущих, обычно начиная с $0$ и $1$. Таким образом, последовательность выглядит следующим образом: $0,1,1,2,3,5,8,13$ и так далее.

Последовательность Фибоначчи имеет следующий вид:

Наибольшее число Фибоначчи, соответствующее типу int, равно

Для $n\le 40$ достаточно воспользоваться типом данных int.

Пусть функция $fib(n)$ вычисляет $n$-ое число Фибоначчи. Тогда мы имеем следующее рекуррентное соотношение:

Теперь давайте реализуем рекурсивную функцию для вычисления чисел Фибоначчи:

# Функция fib вычисляет n-ое число Фибоначчи
def fib(n):
  if (n == 0): return 0
  if (n == 1): return 1
  return fib(n - 1) + fib(n - 2)

# Основная часть программы. Читаем входное значение n
n = int(input())

# Вычисляем и выводим ответ
print(fib(n))

Теперь давайте шаг за шагом разберем, как работает эта рекурсивная функция:

Базовый случай:

• Базовый случай — это когда $n$ равно $0$ или $1$. В этом случае мы знаем числа Фибоначчи: $F_0=0$ и $F_1=1$. Это самый простой случай, когда нам не нужны дальнейшие вычисления.

Шаг рекурсии:

• Для любого другого значения $n$ (когда $n>1$) мы вычисляем число Фибоначчи рекурсивно. Мы делаем это, складывая числа Фибоначчи двух предыдущих значений в последовательности ($fib(n–1)$ и $fib(n–2)$).

• Это означает, что для вычисления $fib(n)$ нам нужно сначала вычислить $fib(n–1)$ и $fib(n–2)$, а затем сложить эти результаты. Этот процесс продолжается до тех пор, пока мы не достигнем базового случая.

Давайте рассмотрим пример.

• Если мы хотим вычислить $fib(4)$, функция вызовет $fib(3)$ и $fib(2)$.

• $fib(3)$ далее вызовет $fib(2)$ и $fib(1)$, а $fib(2)$ вызовет $fib(1)$ и $fib(0)$.

• $fib(1)$ и $fib(0)$ являются базовыми случаями, поэтому они возвращают $1$ и $0$ соответственно.

• Как только мы получим результаты $fib(1)$ и $fib(0)$, $fib(2)$ сложит их вместе $(0+1=1)$.

• $fib(3)$ аналогичным образом сложит результаты $fib(2)$ и $fib(1)(1+1=2)$.

• Наконец, $fib(4)$ сложит $fib(3)$ и $fib(2)(2+1=3)$, и мы получим результат $3$.

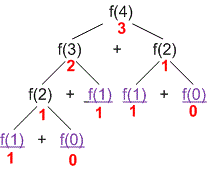
Этот пошаговый процесс демонстрирует, как работают рекурсивные функции. Задача постепенно разбивается на более мелкие подзадачи пока не будут достигнуты базовые случаи, а затем объединяются результаты для решения исходной задачи. И, как мы видели, базовые случаи играют решающую роль в остановке рекурсии и обеспечении отправных точек для наших вычислений.

Обсудите стек вызовов и то, как он используется при рекурсивных вызовах функций

Теперь давайте углубимся в понятие стека вызовов и его использование при рекурсивных вызовах функций. Представьте стек вызовов как стопку тарелок в кафетерии. Когда Вы заходите в кафетерий, Вы берете тарелку и кладете её на верх стопки. Аналогично, когда в программе вызывается функция, информация об этом вызове добавляется в стек вызовов.

Давайте посмотрим, как это работает с рекурсивными вызовами функций:

Вызовы функций и стек вызовов:

• Когда вызывается функция, на вершине стека вызовов создается новый фрейм для хранения информации о вызове этой функции. Он включает в себя параметры функции, локальные переменные и адрес возврата — точку в программе, где должно продолжиться выполнение после вызова функции.

• Каждый раз, когда происходит вызов функции (рекурсивный вызов или обычный вызов функции), новый фрейм добавляется на вершину стека.

Рекурсивные вызовы функций:

• В случае рекурсивных вызовов функция вызывает саму себя внутри своего тела. Это означает, что каждый рекурсивный вызов создает новый фрейм на вершине стека вызовов.

• По мере прогрессирования рекурсии всё больше фреймов добавляется в стек вызовов, и каждый из них представляет собой отдельный экземпляр вызова функции.

• Стек вызовов отслеживает все эти вызовы функций, гарантируя, что программа знает, куда возвращаться после завершения каждого вызова функции.

Базовый случай и разворачивание стека:

• В конечном счете, по мере прогрессирования рекурсии, достигается базовый случай. Он является условием остановки, которое предотвращает бесконечное продолжение рекурсии.

• Когда достигается базовый случай, функция перестает делать дальнейшие рекурсивные вызовы и начинает "разворачивать" стек вызовов.

• Каждый фрейм снимается с вершины стека вызовов, и программа возвращается в точку, где функция была первоначально вызвана. Этот процесс продолжается до тех пор, пока весь стек вызовов не будет полностью развёрнут.

Вопросы памяти:

• Важно отметить, что стек вызовов имеет ограниченный размер, и чрезмерная рекурсия может привести к ошибке переполнения стека, если стек становится слишком глубоким.

• Поэтому при написании рекурсивных функций важно убедиться, что существует корректный базовый случай, чтобы предотвратить бесконечную рекурсию, и ограничить глубину рекурсии, чтобы избежать переполнения стека.

Итак, стек вызовов играет важную роль в управлении вызовами функций, включая рекурсивные вызовы. Он отслеживает последовательность вызовов функций и гарантирует, что программа знает, куда вернуться после завершения каждого вызова функции. Понимание стека вызовов необходимо для понимания работы рекурсии и для написания эффективных и безошибочных рекурсивных функций.

Разъяснить концепцию бесконечной рекурсии и способы ее избежания

Теперь давайте проясним концепцию бесконечной рекурсии и обсудим, как ее избежать.

Бесконечная рекурсия:

• Бесконечная рекурсия происходит, когда рекурсивная функция вызывает саму себя бесконечно, не достигая базового случая, который бы ее остановил.

• Другими словами, функция продолжает делать рекурсивные вызовы, не продвигаясь к базовому случаю, что приводит к бесконечному циклу вызовов функции.

• Бесконечная рекурсия может быстро потребить все доступные системные ресурсы и вызвать аварийное завершение программы или её зависание на неопределенное время.

Как это происходит:

• Бесконечная рекурсия обычно возникает, когда в рекурсивной функции отсутствует или неправильно указан базовый случай.

• Без базового случая или с базовым случаем, который никогда не достигается из-за неправильной логики, функция будет вызывать саму себя бесконечно.

Пример:

Давайте рассмотрим простой пример рекурсивной функции для обратного отсчета от заданного числа:

def countDown(n):
  # Вывод текущего числа
  print(n)
  # Вызов функции countDown с на 1 меньшим аргументом
  countDown(n - 1)

# Пример использования:
countDown(5)  # Вывод чисел с 5 до минус бесконечности

В этой программе нет базового случая остановки рекурсии, поэтому функция будет продолжать каждый раз вызывать себя с меньшим значением $n$, что приводит к бесконечной рекурсии.

Как избежать бесконечную рекурсию:

• Чтобы избежать бесконечной рекурсии, важно убедиться, что каждая рекурсивная функция имеет правильный базовый случай.

• Базовый случай должен представлять собой условие, при котором функция прекращает дальнейшие рекурсивные вызовы и возвращает результат.

• При написании рекурсивной функции всегда спрашивайте себя: "Какое условие должно заставить функцию остановиться и вернуть результат?"

• Убедитесь, что базовый случай достижим и что рекурсивные вызовы ведут к нему.

Исправленный пример:

• Давайте исправим предыдущий пример, добавив базовый случай для остановки рекурсии, когда $n$ достигает $0$:

def countDown(n):
  # Базовый случай
  if n == 0: return
  # Вывод текущего числа
  print(n)
  # Вызов функции countDown с на 1 меньшим аргументом
  countDown(n - 1)

# Пример использования:
countDown(5)  # Вывод чисел с 5 до 1

• Теперь функция прекратит вызывать саму себя, когда $n$ станет $0$. Что и предотвратит бесконечную рекурсию.

Итак, бесконечная рекурсия происходит, когда рекурсивная функция вызывает саму себя бесконечно, не достигая базового случая. Чтобы этого избежать, всегда убеждайтесь, что Ваши рекурсивные функции имеют правильный базовый случай, который останавливает рекурсию и возвращает результат. Тестирование рекурсивных функций с разными входными значениями может помочь выявить потенциальные случаи бесконечной рекурсии во время разработки.

Реализация рекурсивных алгоритмов

Представим серию задач по программированию, подходящих для рекурсии

Давайте обсудим некоторые известные рекурсивные алгоритмы.

Задачу можно решить со сложностью $O(n)$. Для этого достаточно написать наивный цикл for:

# Читаем входные данные
x, n, m = map(int,input().split())

# Инициализируем переменную res значением 1.
# В этой переменной будем вычислять результат x^n mod m
res = 1

# Вычисляем значение x^n mod m используя n операций умножений 
# 1 * x * x * ... * x
for i in range(1,n+1):
  res = (res * x) % m

# Выводим ответ
print(res)

Такая реализация алгоритма превышает Time Limit. Поскольку $n\le 10^9$, а временной лимит для этой задачи составляет всего $1$ секунду, то Вы не сможете выполнить $10^9$ операций за $1$ секунду, даже используя современные компьютеры.

Как мы можем ускорить процесс умножения? Например, если мы хотим вычислить $x^{100}$, то можем представить это выражение в виде $(x^2{)}^{50}$. Используя всего лишь одно умножение для вычисления $x^2$, мы можем эффективно уменьшить степень вдвое: с $100$ до $50$.

Например, вместо использования $16$ умножений для нахождения $x^{16}$, мы можем переписать выражение следующим образом: $x^{16}=(((x^2{)}^2{)}^2{)}^2$, таким образом выполняя всего $4$ умножения. Аналогично можно утверждать, что для вычисления $x^{1024}$ достаточно выполнить всего $10$ умножений.

Если показатель степени нечетный, например, $n=99$, то значение $x^{99}$ вычисляем как $x\cdot x^{98}$.

Например, $x^{15}=((x^2\cdot x{)}^2\cdot x{)}^2\cdot x$.

Мы подошли к методу бинарного возведения в степень, технике, используемой для эффективного вычисления больших степеней числа. Он основан на принципе, что любое число, возведенное в степень, можно выразить как последовательность степеней двойки.

По заданным основанию $x$ и показателю степени $n$, мы выражаем $n$ как сумму степеней двойки. Например, если $n=13$, мы можем записать это как $13=8+4+1$. Затем мы вычисляем $x^n$, умножая вместе значения $x$, возведенные в каждую степень двойки, и объединяем результаты.

Допустим, мы хотим вычислить $x^{13}$.

• Выразим $13$ в двоичной системе: $13=1101$ в двоичном представлении.

• Затем вычислим $x^1$, $x^4$ и $x^8$ (соответствующие установленным битам в двоичном представлении $13$).

• Наконец, перемножаем эти значения: $x^{13}=x^1\cdot x^4\cdot x^8$.

Преимущества. Бинарное возведение в степень сокращает количество необходимых умножений по сравнению с наивным возведением в степень. Оно особенно эффективно для больших степеней, поскольку требует всего $O(lo{g}_{2}n)$ умножений вместо $O(n)$ умножений.

Чтобы найти значение $x^{n}modm$, мы будем использовать формулу:

# Функция myPow вычисляет значение x^n mod m
def myPow(x, n, m):
  if (n == 0): return 1
  if (n % 2 == 0): return myPow((x * x) % m, n / 2, m)
  return (x * myPow(x, n - 1, m)) % m

# Основная часть программы. Читаем входные данные
x, n, m = map(int, input().split())

# Вычисляем и выводим ответ
print(myPow(x, n, m))

В Python имеется встроенная функция $pow(x,n,m)$, которая вычисляет $x^{n}modm$. Предыдущий код можно переписать следующим образом:

# Читаем входные данные
x, n, m = map(int, input().split())

# Вычисляем и выводим ответ
print(pow(x, n, m))

Наибольший общий делитель (НОД) двух целых чисел $a$ и $b$ — это наибольшее положительное число, которое делит и $a$, и $b$ без остатка.

Пример:

• Рассмотрим два числа $a=12$ и $b=18$.

• Делителями числа $12$ будут $1,2,3,4,6$ и $12$.

• Делителями числа $18$ будут $1,2,3,6,9$ и $18$.

• Общими делителями чисел $12$ и $18$ будут $1,2,3$ и $6$.

• Из этих делителей наибольшим будет $6$.

• Поэтому $НОД(12,18)=6$.

Свойства:

• НОД является всегда неотрицательным целым числом.

• Если $a$ и $b$ оба нули, то $НОД(a,b)=0$.

• Если $a$ или $b$ (или оба) отрицательны, то $НОД(a,b)$ равен НОД их абсолютных значений.

• Если $a$ или $b$ равно нулю, то $НОД(a,b)$ равно абсолютному значению ненулевого целого числа.

• НОД любого числа и $0$ равно абсолютному значению этого числа.

Приложения:

• НОД используется в различных математических вычислениях, включая упрощение дробей и нахождение наименьшего общего знаменателя.

• НОД используется в криптографических алгоритмах, таких как RSA, для генерации ключей и шифрования.

• НОД также используется в алгоритмах информатики, таких как алгоритм Евклида для эффективного вычисления.

Алгоритм Евклида — это эффективный метод нахождения НОД двух целых чисел. Он основан на принципе, что НОД двух чисел остаётся неизменным, если мы будем вычитать меньшее число из большего до тех пор, пока одно из них не станет равно нулю.

Если вместо операции "минус" использовать операцию "mod", то вычисления будут проходить быстрее.

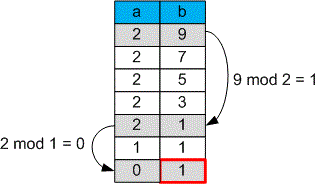
Например, чтобы вычислить $НОД(1,10^9)$ с помощью вычитания, потребуется выполнить $10^9$ операций. Однако при использовании операции взятия остатка достаточно только одного действия.

Для двух целых чисел $a$ и $b$, где $a\ge b$, мы повторяем следующие шаги:

• Если $b$ равно нулю, то НОД равен $a$.

• В противном случае мы заменяем $a$ на $b$, а $b$ на остаток от деления $a$ на $b$. Это можно выразить как $a\leftarrow b$ и $b\leftarrow amodb$.

• Мы продолжаем этот процесс, пока $b$ не станет равно нулю.

НОД $a$ и $b$ — это значение $a$, когда $b$ становится равным нулю.

Алгоритм Евклида эффективен, с временной сложностью $O(lo{g}_{2}min(a,b))$. Он гарантированно завершается, так как значение $b$ уменьшается с каждой итерацией и в итоге становится равным нулю.

НОД двух чисел можно вычислить, используя следующую формулу:

def gcd(a, b):
  if a == 0: return b
  if b == 0: return a
  if a > b: return gcd(a % b, b)
  return gcd(a, b % a)

# Основная часть программы. Читаем входные данные.
a, b = map(int, input().split())

# Вычисляем и выводим НОД двух чисел.
print(gcd(a, b))

Данную формулу можно выразить в другой форме:

def gcd(a, b):
  if b == 0: return a
  return gcd(b, a % b)

# Основная часть программы. Читаем входные данные. 
a, b = map(int, input().split())

# Вычисляем и выводим НОД двух чисел.
print(gcd(a, b))

В Питоне имеется встроенная функция $gcd(a,b)$, которая вычисляет наибольший общий делитель двух чисел. Предыдущий код можно переписать следующим образом:

import math

# Читаем входные данные.
a, b = map(int, input().split())

# Вычисляем и выводим НОД двух чисел.
print(math.gcd(a, b))

Список задач

Рекурсивные программы:

• 1603. Сумма цифр числа

• 1658. Факториал (использовано в лекции)

• 2999. Функция – 10

• 8609. Рекурсия – 1

• 11249. Рекурсия – 2

Числа Фибоначчи:

• 3258. Последовательность Фибоначчи (использовано в лекции)

• 8295. Генерация строк Фибоначчи

НОД / НОК:

• 136. Отрезок

• 1601. НОД двух чисел (использовано в лекции)

• 1602. НОК двух чисел

• 2214. Функция 9

• 7363. Сумма дробей

Биномиальный коэффициент:

• 3260. Сколько?

Возведение в степень:

• 273. Возведение в степень

• 5198. Возведение в степень (использовано в лекции)

• 9644. Сумма степеней

• 9646. Сумма степеней 2