Разбор

Построим $0-1$ граф, присвоив имеющимся рёбрам вес $0$, а их обратным рёбрам — вес $1$. Затем запустим поиск в ширину. Длина кратчайшего пути из вершины $1$ в вершину $n$ будет равна минимальному количеству рёбер, которые нужно обратить.

Пример

Граф, приведенный в примере, выглядит следующим образом:

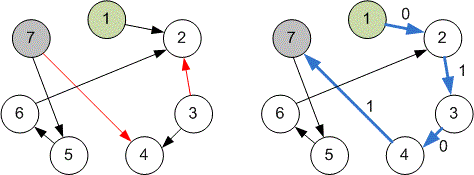
Реализация алгоритма

Объявим константу бесконечность.

#define INF 0x3F3F3F3F

Объявим массив кратчайших расстояний $dist$ и список смежности графа $g$. Для каждого ребра вместе со смежной вершиной храним вес ребра ($0$ или $1$).

vector<int> dist;
vector<vector<pair<int, int> > > g;

Функция bfs реализует поиск в ширину из вершины $start$.

void bfs(int start)
{
  dist = vector<int>(n + 1, INF);
  dist[start] = 0;

  deque<int> q;
  q.push_back(start);

  while (!q.empty())
  {
    int v = q.front(); q.pop_front();
    for (auto edge : g[v])
    {
      int to = edge.first;
      int w = edge.second;
      if (dist[to] > dist[v] + w)
      {
        dist[to] = dist[v] + w;

В зависимости от веса ребра $w$ добавляем вершину $to$ в конец или в начало очереди.

        if (w == 1)
          q.push_back(to);
        else
          q.push_front(to);
      }
    }
  }
}

Основная часть программы. Читаем входные данные.

scanf("%d %d", &n, &m);
g.resize(n + 1);
for (i = 0; i < m; i++)
{
  scanf("%d %d", &a, &b);

Ориентированному ребру $a\to b$ присваиваем вес $0$, обратному ребру присваиваем вес $1$.

  g[a].push_back({ b, 0 });
  g[b].push_back({ a, 1 });
}

Запускаем поиск в ширину из вершины $1$.

bfs(1);

Выводим ответ — кратчайшее расстояние до вершины $n$.

if (dist[n] == INF)
  printf("-1\n");
else
  printf("%d\n", dist[n]);