Разбор

При помощи поиска в глубину вычислим XOR сумму между вершиной $1$ и всеми остальными вершинами. XOR сумму между вершинами $1$ и $v$ занесем в $x[v]$. Пусть $ones$ — количество единиц, а $zeroes$ — количество нулей в массиве $x(ones+zeroes=n)$. Тогда ответом на задачу будет число $ones\cdot zeroes$.

Пример

Рассмотрим граф, приведенный в примере.

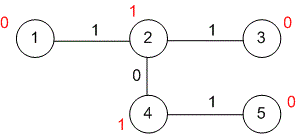
Возле каждой вершины $v$ записана XOR сумма $x[v]$ между $1$ и $v$. Если $x[v]=x[u]$ для некоторых вершин $v$ и $u$, то XOR сумма между ними равна $0$, таким образом совершая вклад $0$ в общую сумму. XOR сумма для каждой пары вершин $(v,u)$, для которой $x[v]\ne x[u]$, дает вклад $1$ в общую сумму.

Следовательно ответ равен количеству пар вершин $(v,u)$, для которых $x[v]\ne x[u]$. Это число равно $ones\cdot zeroes=2\cdot 3=6$. Парами вершин, дающими $1$ в общую сумму, будут: $(1,2),(1,4),(2,3),(2,5),(3,4),(4,5)$.

Реализация алгоритма

Входной граф храним в списке смежности $g$. Объявим массив $x$.

vector<vector<pair<int,int> > > g;
vector<int> x;

Функция dfs реализует поиск в глубину, который вычисляет XOR сумму $x[v]$ между вершинами $1$ и $v$. Текущая XOR сумма между $1$ и $v$ равна $cur\_xor$. Предком вершины $v$ является $p$.

void dfs(int v, int cur_xor, int p = -1)
{
  x[v] = cur_xor;
  for (auto z : g[v])
  {
    int to = z.first;
    int w = z.second;
    if (to != p) dfs(to, cur_xor ^ w, v);
  }
}

Основная часть программы. Читаем входной граф.

scanf("%d", &n);
g.resize(n + 1);
x.resize(n + 1);

for (i = 1; i < n; i++)
{
  scanf("%d %d %d", &u, &v, &d);
  g[u].push_back(make_pair(v, d));
  g[v].push_back(make_pair(u, d));
}

Запускаем поиск в глубину из вершины $1$.

dfs(1, 0, -1);

Вычисляем количество нулей $zeroes$ и единиц $ones$ в массиве $x$.

ones = 0;
for (i = 1; i <= n; i++)
  if (x[i] == 1) ones++;
zeroes = n - ones;

Выводим ответ.

printf("%lld\n", 1LL * ones * zeroes);

Python реализация

Функция dfs реализует поиск в глубину, который вычисляет XOR сумму $x[v]$ между вершинами $1$ и $v$. Текущая XOR сумма между $1$ и $v$ равна $cur\_xor$. Предком вершины $v$ является $p$.

def dfs(v, cur_xor = 0, p = -1):
  x[v] = cur_xor
  for to, w in g[v]:
    if to != p:
      dfs(to, cur_xor ^ w, v)

Основная часть программы. Читаем входной граф.

n = int(input())
g = [[] for _ in range(n + 1)]
for _ in range(n - 1):
  u, v, d = map(int, input().split())
  g[u].append((v, d))
  g[v].append((u, d))

Инициализируем массив $x$.

x = [0] * (n + 1)

Запускаем поиск в глубину из вершины $1$.

dfs(1)

Вычисляем количество нулей $zeroes$ и единиц $ones$ в массиве $x$.

ones = sum(x)
zeroes = n - ones

Выводим ответ.

print(ones * zeroes)