Разбор

Пусть массив $m$ содержит точки распила: $m_{1}, ..., m_{n}$ . Добавим начальную и конечную точки: $m_{0} = 0, m_{n + 1} = l$ .

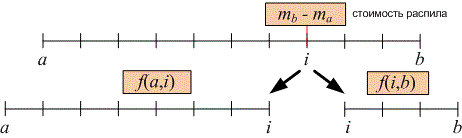
Пусть функция $f (a, b)$ возвращает минимальную стоимость распила куска палки от $m_{a}$ до $m_{b}$ с учётом необходимых точек распила, находящихся внутри отрезка. Внутри отрезка $[m_{a}; m_{a + 1}]$ точек распила нет, поэтому $f (a, a + 1) = 0$ . Ответом на задачу будет значение $f (0, n + 1)$ . Вычисленные значения $f (a, b)$ сохраняем в ячейках массива $d p [a] [b]$ .

Пусть отрезок палки $[m_{a}, m_{b}]$ следует распилить на несколько частей. Если первый распил мы произведем в точке $m_{i} (a < i < b)$ , то стоимость самого распила составит $m_{b} - m_{a}$ . Далее следует распилить оставшиеся куски соответственно за цену $f (a, i)$ и $f (i, b)$ . Значение $i$ следует выбрать так, чтобы минимизировать суммарную стоимость:

f (a, b) = a < i < b min (f (a, i) + f (i, b)) + m_{b} - m_{a}

Пример

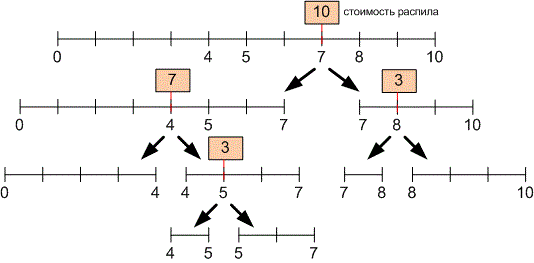
Рассмотрим второй тест. Приведем один из возможных методов распила палки длины $10$ стоимостью $10 + 7 + 3 + 3 = 23$ :

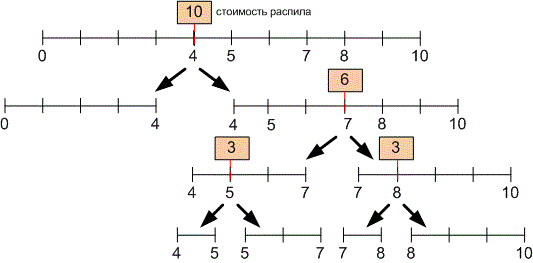
Рассмотрим оптимальный метод распила стоимостью $10 + 6 + 3 + 3 = 22$ :

Реализация алгоритма

Объявим константы и рабочие массивы.

#define MAX 55
#define INF 0x3F3F3F3F
int dp[MAX][MAX];
int m[MAX];

Функция $f (a, b)$ возвращает минимальную стоимость разреза куска палки на отрезке $[a; b]$ с учётом точек распила, находящихся внутри этого отрезка.

int f(int a, int b)
{

Если $a + 1 = b$ , то внутри отрезка $[a; b]$ точек разреза нет. Возвращаем $0$ .

  if (b - a == 1) return 0;

Если значение $f (a, b)$ уже вычислено, то возвращаем его.

  if (dp[a][b] != INF) return dp[a][b];

Совершаем разрез в точке $i (a < i < b)$ . Вычисляем стоимость следующим образом:

f (a, b) = a < i < b min (f (a, i) + f (i, b)) + m_{b} - m_{a}

  for (int i = a + 1; i < b; i++)
    dp[a][b] = min(dp[a][b], m[b] - m[a] + f(a, i) + f(i, b));

Возвращаем результат $f (a, b) = d p [a] [b]$ .

  return dp[a][b];
}

Основная часть программы. Читаем входные данные для каждого теста.

while(scanf("%d",&l),l)
{
  scanf("%d",&n);

Добавим начальную и конечную точки распила: $m_{0} = 0, m_{n + 1} = l$ .

  m[0] = 0; m[n+1] = l;
  for(i = 1; i <= n; i++)
    scanf("%d",&m[i]);

Инициализируем массив $d p$ .

  memset(dp,0x3F,sizeof(dp));

Вычисляем и выводим ответ.

  printf("The minimum cutting is %d.\n",f(0,n+1));
}