Разбор

Рассмотрим, какие значения принимает выражение $f(i,j)=i/n-j/m$, где $i,j\in Z$ при фиксированных $n$ и $m$. Например, $f(n,m)=n/n-m/m=0$.

Рассмотрим, например, функцию $f(i,j)=i/3-j/5$. Тогда

Согласно расширенному алгоритму Евклида, всегда существуют такие целые $i$ и $j$, что $i/3-j/5=1$. Следовательно, наименьшим положительным значением, которое может принимать выражение $i/3-j/5$, является $1/15$. Отсюда следует, что это выражение может принимать все возможные значения вида $k/15$, где $k\in Z$.

Теорема. Если $f(i,j)=i/n-j/m$, то эта функция принимает значения вида $k/НОК(n,m)$, где $k\in Z$.

Доказательство. Действительно,

Поскольку числа $m/НОД(n,m)$ и $n/НОД(n,m)$ являются взаимно простыми, то всегда существуют такие $i$ и $j$, что числитель дроби равен $1$. Следовательно, функция $f(i,j)$ может принимать все возможные значения вида $k/НОК(n,m)$, где $k\in Z$.

Теперь рассмотрим исходную функцию

Ее значения — расстояния от точки $t$ до ближайшей точки вида $k/НОК(n,m),k\in Z$. Для максимизации функции $f(t)$ значение $t$ следует выбрать таким образом, чтобы оно находилось точно посередине между соседними точками $k/НОК(n,m)$ и $(k+1)/НОК(n,m)$, где $k$ — целое число. Значение функции в такой точке равно $1/2\cdot НОК(n,m)$, что и будет ответом.

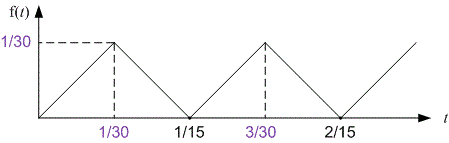
Пример

Пусть $f(t)=mi{n}_{i,j\in Z}|\frac{i}{3}-\frac{j}{5}+t|$. Очевидно, что $f(0)=0$. Равенство $f(1/15)=0$ справедливо, так как существуют такие $i$ и $j$, что $i/3-j/5=-1/15$ (например, $i=1,j=2$). Из этого также следует, что $f(k/15)=0$, где $k\in Z$.

Однако $f(k/15+1/30)=1/30$, и это будет наибольшим значением функции, так как точка $k/15+1/30$ находится на максимальном расстоянии от нулей функции.

Реализация алгоритма

Функция gcd вычисляет наибольший общий делитель чисел $a$ и $b$.

long long gcd(long long a, long long b)
{
  return b == 0 ? a : gcd(b, a % b);
}

Функция lcm вычисляет наименьшее общее кратное чисел $a$ и $b$.

long long lcm(long long a, long long b)
{
  return a / gcd(a, b) * b;
}

Основная часть программы. Читаем входные данные.

while (scanf("%lld %lld", &n, &m) == 2)
{

Вычисляем и выводим ответ.

  d = 2 * lcm(n, m);
  printf("%lld/%lld\n", 1, d);
}