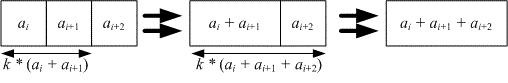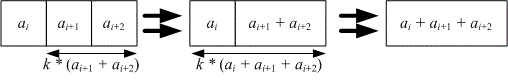Разбор

Пусть $f (i, j)$ — минимальная стоимость, за которую можно свести массив $[a_{i}, ..., a_{j}]$ до одного элемента. Это значение будем хранить в ячейке $d p [i] [j]$ .

Очевидно, что $f (i, i) = 0$ .

Из условия задачи следует, что

f (i, i + 1) = k \cdot (a_{i} + a_{i + 1})

Вычислим значение $f (i, i + 2)$ . Объединение трех чисел в одно можно совершить двумя способами:

Объединить $a_{i}$ и $a_{i + 1}$ за $k \cdot (a_{i} + a_{i + 1})$ , после чего объединить $a_{i} + a_{i + 1}$ и $a_{i + 2}$ за $k \cdot (a_{i} + a_{i + 1} + a_{i + 2})$ .
Объединить $a_{i + 1}$ и $a_{i + 2}$ за $k \cdot (a_{i + 1} + a_{i + 2})$ , после чего объединить $a + i$ и $a_{i + 1} + a_{i + 2}$ за $k \cdot (a_{i} + a_{i + 1} + a_{i + 2})$ .

Таким образом

f (i, i + 2) = min (k \cdot (a_{i} + a_{i + 1}) + k \cdot (a_{i} + a_{i + 1} + a_{i + 2}), k \cdot (a_{i + 1} + a_{i + 2}) + k \cdot (a_{i} + a_{i + 1} + a_{i + 2}))

Теперь рассмотрим вычисление значения $f (i, j)$ . Для преобразования массива $[a_{i}, ..., a_{j}]$ в один элемент, который будет равен $a_{i} + ... + a_{j}$ , следует выбрать некоторое значение $p (i \leq p < j)$ , рекурсивно решить задачу для массивов $[a_{i}, ..., a_{p}]$ и $[a_{p + 1}, ..., a_{j}]$ , после чего объединить элементы $a_{i} + ... + a_{p}$ и $a_{p + 1} + ... + a_{j}$ . Значение $p$ следует выбрать таким образом, чтобы стоимость преобразования была минимальной:

f (i, j) = i \leq p < j min (f (i, p) + f (p + 1, j)) + k \cdot (a_{i} + ... + a_{j})

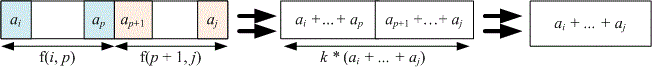
Для быстрых вычислений сумм $a_{i} + ... + a_{j}$ воспользуемся массивом префиксных сумм $p re f$ , в котором

p re f [i] = a_{1} + ... + a_{i},

откуда $a_{i} + ... + a_{j} = p re f [j] - p re f [i - 1]$ .

Реализация алгоритма

Объявим рабочие массивы.

#define MAX 101
#define INF 0x3F3F3F3F
int dp[MAX][MAX], a[MAX], pref[MAX];

Функция $f (i, j)$ возвращает минимальную стоимость, за которую можно преобразовать массив $[a_{i}, ..., a_{j}]$ к одному элементу.

int f(int i, int j)
{
  if (dp[i][j] == INF)
    for (int p = i; p < j; p++)
      dp[i][j] = min(dp[i][j], f(i, p) + f(p + 1, j) + (pref[j] - pref[i - 1]) * k);
    return dp[i][j];
}

Основная часть программы. Читаем входные данные.

scanf("%d %d", &n, &k);
memset(dp, 0x3F, sizeof(dp));
for (i = 1; i <= n; i++)
{
  scanf("%d", &a[i]);
  dp[i][i] = 0;

Вычисляем массив префиксных сумм.

  pref[i] = pref[i - 1] + a[i];
}

Вычисляем и выводим ответ.

printf("%d\n", f(1, n));

Python реализация

Объявим константу бесконечность.

INF = float('inf')

def f(i, j):
  if dp[i][j] == INF:
    for p in range(i, j):
      dp[i][j] = min(dp[i][j], f(i, p) + f(p + 1, j) + (pref[j] - pref[i - 1]) * k)
  return dp[i][j]

Основная часть программы. Читаем входные данные.

n, k = map(int, input().split())
a = [0] + list(map(int, input().split()))

Вычисляем массив префиксных сумм.

pref = [0] * (n + 1)
for i in range(1, n + 1):
  pref[i] = pref[i - 1] + a[i]

Инициализируем массив $d p$ .

dp = [[INF] * (n + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
  dp[i][i] = 0

Вычисляем и выводим ответ.

print(f(1, n))