Разбор

Отсортируем дороги (ребра графа) по возрастанию их опасности. Для решения задачи будем использовать систему непересекающихся множеств. Изначально образуем $n$ множеств, каждое из которых содержит одну вершину. Просматриваем ребра в порядке возрастания опасности. Для каждого ребра $(a, b)$ объединяем множества, содержащие вершины $a$ и $b$ . Как только вершины $1$ и $n$ попадут в одно множество, алгоритм завершается. В этом случае путь от первой вершины до $n$ -ой уже будет существовать, причем опасности дорог, через которые проходит этот путь, будут не большими чем опасность последней рассмотренной дороги.

Таким образом если после рассмотрения ребра $(x, y)$ представители вершин $1$ и $n$ совпадут, то опасность самого безопасного маршрута будет равна опасности дороги $(x, y)$ .

Пример

В первом тесте опасность самого безопасного маршрута равна $1$ .

Рассмотрим второй тест.

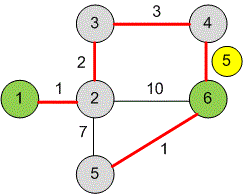
Ребра обрабатываются в порядке возрастания их опасности. Как только будет обработано ребро с опасностью $5$ , вершины $1$ и $6$ соединятся и алгоритм останавливается.

Реализация алгоритма

Объявим массив $ma s$ , используемый системой непересекающихся множеств. В массиве $e$ будем хранить ребера графа.

#define MAX 1000001
int mas[MAX];
struct Edge
{
  int x, y, danger;
} e[MAX];

Функция Repr находит представителя множества, в котором находится вершина $n$ . При этом для избежания вердикта Time Limit используется эвристика: если представителем вершины $n$ является $x$ , то следует положить $ma s [n] = x$ .

int Repr(int n)
{
  if (n == mas[n]) return n;
  return mas[n] = Repr(mas[n]);
}

Функция Union объединяет множества, содержащие вершины $x$ и $y$ .

int Union(int x,int y)
{
  int x1 = Repr(x),y1 = Repr(y);
  mas[x1] = y1;
  return (x1 != y1);
}

Объявим компаратор lt для сравнения ребер. Дороги сортируются по возрастанию их опасности.

int lt(Edge a, Edge b)
{
  return (a.danger < b.danger);
}

Основная часть программы. Читаем количество городов $n$ и дорог $m$ .

scanf("%d %d",&n,&m);

Инициализируем массив $ma s$ .

for(i = 1; i <= n; i++) mas[i] = i;

Читаем ребра графа в массив $e$ .

for(i = 0; i < m; i++)
  scanf("%d %d %d",&e[i].x,&e[i].y,&e[i].danger);

Сортируем ребра по возрастанию опасности.

sort(e,e+m,lt);

Переберем ребра, начиная с наименее опасного. Объединяем множества, содержащие их вершины. Как только вершины $1$ и $n$ попадут в одно множество ( $R e p r (1)$ станет равным $R e p r (n)$ ), самый безопасный путь будет найден. Его опасность будет равна опасности последнего обрабатываемого ребра, то есть $e [i] . d an g er$ .

for(i = 0; i < m; i++)
{
  Union(e[i].x,e[i].y);
  if (Repr(1) == Repr(n)) break;
}

Выводим результат.

printf("%d\n",e[i].danger);

Java реализация

import java.util.*;

class Edge
{
  int x, y, danger;
  Edge (int x, int y, int danger)
  {
    this.x = x;
    this.y = y;
    this.danger = danger;
  }
};

public class Main
{
  static int mas[], size[];
	
  static int Repr(int n)
  {
    if (n == mas[n]) return n;
    return mas[n] = Repr(mas[n]);
  }
	
  static boolean Union(int x,int y)
  {
    x = Repr(x); y = Repr(y);
    if(x == y) return false;

    if (size[x] < size[y])
    {
      int temp = x; x = y; y = temp;
    }
    mas[y] = x;
    size[x] += size[y];
    return true;    
  }
  
  public static class MyFun implements Comparator<Edge>
  {
    public int compare(Edge a, Edge b)
    {
      return a.danger - b.danger;
    }
  }
  
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    int n = con.nextInt();
    int m = con.nextInt();
    mas = new int[n+1];
    size = new int[n+1];
    
    for(int i = 1; i <= n; i++)
    {
      mas[i] = i;
      size[i] = 1;
    }
    
    Vector<Edge> v = new Vector<Edge>();
    for(int i = 0; i < m; i++)
    {
      int x = con.nextInt();
      int y = con.nextInt();
      int dust = con.nextInt();
      v.add(new Edge(x,y,dist));
    }

    Collections.sort(v, new MyFun());
    
    int index = 0;
    for(int i = 0; i < m; i++)
    {
      Union(v.get(i).x,v.get(i).y);
      if (Repr(1) == Repr(n)) 
      {
        index = i;
        break;
      }
    }
    
    System.out.println(v.get(index).danger);
    con.close();
  }
}

Python реализация

Объявим структуру ребро $E d g e$ .

class Edge:
  def __init__(self, x, y, danger):
    self.x = x
    self.y = y
    self.danger = danger

def Repr(n):
  if n == mas[n]:
    return n
  mas[n] = Repr(mas[n])
  return mas[n]

Функция Union объединяет множества, содержащие вершины $x$ и $y$ .

def Union(x, y):
  x1 = Repr(x)
  y1 = Repr(y)
  mas[x1] = y1
  return x1 != y1

Основная часть программы. Читаем количество городов $n$ и дорог $m$ .

n, m = map(int, input().split())

Инициализируем список $ma s$ , используемый системой непересекающихся множеств.

mas = [i for i in range(n + 1)]

Читаем ребра графа в список $e$ .

e = []
for i in range(m):
  x, y, danger = map(int, input().split())
  e.append(Edge(x, y, danger))

Сортируем ребра по возрастанию опасности.

e.sort(key=lambda x: x.danger)

for i in range(m):
  Union(e[i].x, e[i].y)
  if Repr(1) == Repr(n):
    break

Выводим результат.

print(e[i].danger)