Разбор

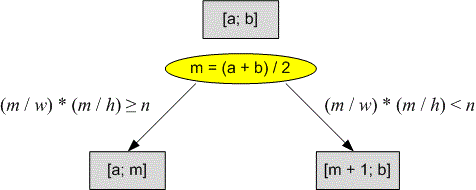
Пусть $x$ — искомая длина стороны квадратной доски. Будем искать $x$ бинарным поиском. Очевидно, что $0<x\le max(w,h)\cdot n$. Поиск начнем на отрезке $[a;b]=[0;max(w,h)\cdot n]$.

Пусть $m=(a+b)/2$ — текущая длина стороны доски. Поскольку диплом имеет размер $w\cdot h$, то на ней можно разместить максимум $(m/w)\cdot (m/h)$ дипломов. Если это число меньше $n$, то размер доски маловат, устанавливаем $a=m+1$. Иначе двигаем правую границу поиска: $b=m$.

Пусть размер диплома $w\times h=2\times 3$.

• На доске $8\times 8$ можно расположить максимум $(8/2)\cdot (8/3)=4\cdot 2=8$ дипломов;

• На доске $9\times 9$ можно расположить максимум $(9/2)\cdot (9/3)=4\cdot 3=12$ дипломов;

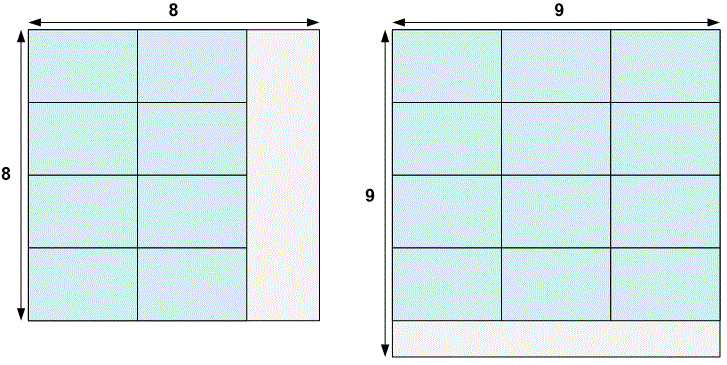
Минимальный размер стороны доски, на которой можно расположить $10$ дипломов, равен $9$.

Реализация алгоритма

Читаем входные данные.

scanf("%lld %lld %lld", &w, &h, &n);

Устанавливаем границы бинарного поиска $[a;b]=[0;max(w,h)\cdot n]$.

a = 0;
b = max(w, h) * n;

Запускаем бинарный поиск.

while (a < b)
{
  m = (a + b) / 2;

Наибольшее количество дипломов размера $w\cdot h$, которое можно расположить на доске со стороной $m$, равно $dip=(m/w)\cdot (m/h)$.

  dip = (m / w) * (m / h);
  if (dip < n) a = m + 1;
  else b = m;
}

Выводим ответ.

printf("%lld\n", b);

Python реализация

Читаем входные данные.

w, h, n = map(int, input().split())

Устанавливаем границы бинарного поиска $[a;b]=[0;max(w,h)\cdot n]$.

a = 0
b = max(w, h) * n

Запускаем бинарный поиск.

while a < b:
  m = (a + b) // 2

Наибольшее количество дипломов размера $w\cdot h$, которое можно расположить на доске со стороной $m$, равно $dip=(m/w)\cdot (m/h)$.

  dip = (m // w) * (m // h)
  if dip < n:
    a = m + 1
  else:
    b = m

Выводим ответ.

print(b)