Интегральные прямоугольники
Рассмотрим прямоугольники, высота h и ширина w которых являются целыми числами. Такие прямоугольники мы называем целочисленными прямоугольниками. В этой задаче мы рассматриваем только широкие целочисленные прямоугольники, то есть те, у которых w > h.
Мы определяем следующий порядок для широких целочисленных прямоугольников. Даны два широких целочисленных прямоугольника:
Прямоугольник с более короткой диагональю считается меньшим.
Если длины диагоналей одинаковы, то прямоугольник с меньшей высотой считается меньшим.
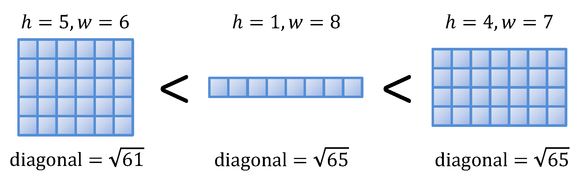
Дан широкий целочисленный прямоугольник. Найдите наименьший широкий целочисленный прямоугольник, который больше данного.
Входные данные
Ввод состоит из нескольких наборов данных. Количество наборов данных не превышает 100. Каждый набор данных описывает широкий целочисленный прямоугольник, указывая его высоту и ширину, а именно h и w, разделенные пробелом в строке:
h w
Для каждого набора данных h и w (> h) являются целыми числами, большими 0 и не превышающими 100.
Конец ввода обозначается строкой из двух нулей, разделенных пробелом.
Выходные данные
Для каждого набора данных выведите в строке два числа, описывающие высоту и ширину, а именно h и w (> h), наименьшего широкого целочисленного прямоугольника, большего описанного в наборе данных. Между числами поставьте пробел. Никакие другие символы в выводе не допускаются.
Для любого широкого целочисленного прямоугольника, заданного во входных данных, ширина и высота наименьшего широкого целочисленного прямоугольника, большего данного, известны как не превышающие 150.
Кроме того, хотя порядок широких целочисленных прямоугольников использует сравнение длин диагоналей, это сравнение может быть заменено сравнением квадратов (самопроизведений) длин диагоналей, что позволяет избежать возможных проблем, связанных с использованием чисел с плавающей запятой.