Досліджуючи рекурсію
Мета цього уроку — познайомити студентів з поняттям рекурсії, зрозуміти її основи та оволодіти її реалізацією в програмуванні. До кінця цього уроку студенти повинні бути здатні:
Дати визначення рекурсії та описати її основні характеристики.
Розібратися в механізмі роботи рекурсивних функцій.
Реалізувати базові рекурсивні алгоритми.
Ідентифікувати ситуації, в яких рекурсія є підходящим рішенням.
Вступ:
Почніть з короткого обговорення методів розв’язання задач у програмуванні.
Наведіть приклад рекурсії з реального життя.
Визначіть рекурсію як техніку програмування, при якій функція викликає саму себе прямо чи опосередковано для розв’язання задачі.
Поясніть ключові характеристики рекурсії: базис, рекурсивний крок і виклик самої себе.
Розуміння рекурсивних функцій:
Поясніть механізм роботи рекурсивних функцій, використовуючи простий приклад (факторіал, обчислення степеня чи послідовність Фібоначчі).
Продемонструйте роботу рекурсивних функцій крок за кроком, підкреслюючи важливість базового випадку.
Обговоріть стек викликів і його використання при рекурсивних викликах функцій.
Поясніть концепцію нескінченної рекурсії та способи її уникнення.
Реалізація рекурсивних алгоритмів:
Представте серію задач з програмування, які підходять для розв'язання за допомогою рекурсії.
Розділіть студентів на пари або невеликі групи для розв'язання цих задач рекурсивним способом.
Заохочуйте студентів писати рекурсивні функції з нуля, приділяючи особливу увагу визначенню базового та рекурсивного випадків.
Слідкуйте за роботою груп, щоб за потреби надавати їм допомогу та поради.
Огляд і практика:
Нехай кожна група представить свої рекурсивні рішення класу.
Обговоріть оптимальність та зрозумілість різних рекурсивних підходів.
Розберіть загальні труднощі та помилки, з якими зіткнулися учасники під час виконання завдання.
Надайте додаткові задачі для практики, щоб студенти могли працювати над ними індивідуально або в групах.
Висновок:
Підсумуйте основні моменти, розглянуті на уроці, підкресливши силу та універсальність рекурсії в програмуванні.
Заохочуйте студентів продовжувати вивчати рекурсію у своїх проєктах і завданнях.
Домашнє завдання:
Дайте домашнє завдання для закріплення вивчених у класі понять. Наприклад, реалізувати рекурсивні алгоритми для конкретних задач або проаналізувати існуючі рекурсивні функції в бібліотеках коду.
Оцінювання:
Оцініть розуміння студентів через їхню участь у дискусіях на семінарах, здатність розв'язувати рекурсивні задачі з програмування та вміння чітко пояснювати рекурсивні рішення.
Перевірте домашні завдання, щоб оцінити індивідуальне засвоєння концепцій рекурсії та навичок їхньої реалізації.
Вступ
Почнемо з короткого обговорення методів розв'язання задач у програмуванні
У програмуванні розв'язання задач є фундаментальною навичкою, яку Ви будете використовувати кожного разу, коли писатимете код. Перш ніж ми заглибимося в особливості рекурсії, давайте поговоримо про методи розв'язання задач.
Думайте про розв'язання задач як про подорож. Ви починаєте з задачі, програму для якої слід написати. І Вам потрібно зрозуміти, як перейти від точки (умови) до точки (розв'язання). Ця подорож включає в себе поділ задачі на менші частини, з якими зручніше працювати, розуміння правил або обмежень, а також розробку плану досягнення бажаного результату.
Існує кілька технік, які програмісти використовують для ефективного розв'язання задач. Ось деякі з них:
Розуміння задачі: перш ніж Ви почнете розв'язувати задачу, Вам необхідно повністю зрозуміти її. Це включає в себе читання та аналіз її умови, визначення вхідних та вихідних даних, а також роз'яснення будь-яких неясностей.
Розділяй і володарюй: багато складних задач можна розв'язати, поділивши їх на менші, простіші підзадачі. Цей підхід, відомий як "розділяй і володарюй", дозволяє Вам розв'язувати кожну підзадачу окремо, а потім комбінувати розв'язання, щоб розв'язати більшу.
Алгоритмічне мислення: алгоритми — це покрокові процедури для розв'язання задач. Коли Ви стикаєтеся із задачею, спробуйте мислити алгоритмічно, розбиваючи розв'язання на послідовність логічних кроків.
Абстракція: абстракція передбачає зосередження на суттєвих деталях задачі, ігноруючи несуттєву або відволікаючу інформацію. Абстрагуючи непотрібні деталі, Ви зможете спростити задачу і зосередитися на важливому.
Ітерація та рекурсія: ітерація передбачає розв'язання задачі шляхом багаторазового виконання циклу або послідовності команд. Рекурсія, з іншого боку, передбачає розв'язання задачі шляхом її поділу на менші екземпляри тієї ж самої задачі. Як ітерація, так і рекурсія є потужними методами розв'язання задач, з якими Ви часто будете стикатися у програмуванні.
Оволодівши зазначеними методами розв'язання задач, Ви будете краще підготовлені до розв'язання широкого спектра задач з програмування, включаючи ті, що пов'язані з рекурсією. Тому, заглиблюючись у вивчення рекурсії, пам'ятайте про ці стратегії розв'язання задач — вони стануть цінними інструментами у Вашому арсеналі програмування.
Приведіть концепцію рекурсії на прикладі з реального життя
Давайте на мить відійдемо від програмування і подумаємо про рекурсію на прикладах з реального життя. Уявіть, що Ви стоїте перед набором російських матрьошок. Ці ляльки бувають різних розмірів, і кожна поміщається всередину наступної, більшої за розміром.
Тепер давайте подумаємо, як Ви могли б описати процес відкриття кожної матрьошки в наборі. Починаєте Ви з найбільшої, і коли її відкриваєте, то знаходите всередині меншу матрьошку. Потім Ви відкриваєте цю меншу матрьошку і знаходите всередині ще меншу, і так далі, поки не досягнете найменшої — тієї, яка не містить всередині себе інших матрьошок.
Процес відкриття кожної матрьошки можна вважати рекурсивним. Чому? Тому що кожна матрьошка має схожу структуру з іншими, і дія по її відкриттю однакова для кожної – вона включає в себе погляд усередину, щоб побачити, чи є там менша матрьошка.
У термінах програмування рекурсія працює аналогічно. Замість відкриття російських матрьошок ми "відкриваємо" функції або методи. Рекурсивна функція — це функція, яка викликає саму себе, або прямо, або опосередковано, щоб розв'язати задачу, поділивши її на менші екземпляри тієї ж самої задачі.
Як і з матрьошками, рекурсія розв'язує задачу шляхом її поділу на менші, подібні підзадачі, доти, поки ми не досягнемо точки, де задача стає настільки малою і простою, що ми можемо розв'язати її безпосередньо. Ця найменша і найпростіша версія задачі називається базовим випадком.
Розуміючи рекурсію через приклади з реального життя, такі як російські матрьошки, ми бачимо, як вона застосовується у програмуванні, і наскільки вона може бути потужним інструментом для розв'язання складних задач. Тому, заглиблюючись у вивчення рекурсії, тримайте цю візуальну аналогію в умі — вона допоможе Вам інтуїтивно зрозуміти концепцію.
Визначте рекурсію як метод програмування, при якому функція викликає саму себе прямо чи опосередковано для розв'язання задачі
Тепер давайте спростимо визначення рекурсії. Уявіть, що у Вас є функція — набір інструкцій, що виконують певну задачу у Вашій програмі. А тепер уявіть, що ця функція може викликати саму себе. Так, Ви не ослухалися! Це і називається рекурсією.
Рекурсія схожа на цикл, але замість того, щоб повторювати набір інструкцій до тих пір, поки не буде виконано умову, рекурсивна функція повторює саму себе, викликаючи саму себе — прямо чи опосередковано — до тих пір, поки не досягне певної умови, зазвичай званої базовим випадком.
Дозвольте пояснити це на прикладі. Уявіть, що у Вас є функція "countDown", яка виводить числа від до . Замість використання циклу ми можемо визначити "countDown" рекурсивно. Ось як це працює:
На вхід функції "countDown" подається число .
Якщо число дорівнює (базовий випадок), то функція виводить "" і завершується.
Якщо число більше , то функція виводить поточне число, а потім викликає саму себе з меншим наступним числом.
Цей процес триває до тих пір, поки функція не досягне базового випадку, після чого вона перестає викликати саму себе, і рекурсія "розгортається" назад до вихідного виклику.
def countDown(n):
# Базовий випадок: якщо n = 1, то виводимо його та зупиняємо рекурсію
if n == 1:
print(n)
else:
# Виводимо поточне число
print(n)
# Викликаємо функцію countDown з наступним меншим числом
countDown(n - 1)
# Приклад визову:
countDown(5) # Вивести числа від 5 до 1 по спаданнюТаким чином, рекурсія — це спосіб розв'язання задач шляхом поділу їх на менші, подібні підзадачі, а потім розв'язання цих підзадач шляхом багаторазового виклику однієї і тієї ж функції, поки ми не досягнемо базового випадку, де задачу можна розв'язати безпосередньо.
Майте на увазі, що рекурсія може спочатку здаватися трохи заплутаною, але з практикою і розумінням її принципів Ви зможете використовувати її як потужний інструмент у своїх уроках з програмування.
Виділіть ключові характеристики рекурсії: базис, рекурсивний крок і виклик самої себе
Тепер, коли ми розуміємо, що таке рекурсія і як вона працює, давайте заглибимося в її ключові характеристики. Рекурсія схожа на добре налагоджений механізм — у неї є певні частини, які працюють разом, щоб забезпечити її функціонування. Ось три ключові характеристики рекурсії, на яких ми зупинимося: базис, рекурсивний виклик і виклик самої себе.
Базис:
Уявіть базис рекурсії як точку зупинки для рекурсивної функції. Це умова, яка вказує функції, коли припинити викликати саму себе і почати повертати значення.
Без базису рекурсивна функція продовжувала б викликати саму себе нескінченно, що призвело б до так званої нескінченної рекурсії, чого ми не бажаємо.
У попередньому прикладі з функцією “countDown” базовим був випадок, коли ставало рівним . У цей момент ми просто виводили і припиняли виклик функції.
Крок рекурсії:
Рекурсивний крок є тим місцем, де відбувається магія рекурсії. Це частина функції, в якій ми викликаємо саму функцію.
Кожного разу, коли функція здійснює рекурсивний виклик, ми на крок наближаємось до базового випадку. Ми розбиваємо задачу на все менші і менші підзадачі, поки не досягнемо базового випадку.
У функції "countDown" рекурсивний крок виконується, коли більше . Ми виводимо поточне значення , а потім знову викликаємо функцію "countDown" з аргументом .
Виклик самої себе:
Ця характеристика може звучати складно, але насправді вона доволі проста. Самовиклик означає, що функція викликає саму себе.
Коли ми визначаємо рекурсивну функцію, ми по суті кажемо: "Гей, функція, ти можеш викликати саму себе, якщо це необхідно".
Природа самовиклику дозволяє рекурсії розв'язувати складні задачі, розбиваючи їх на менші екземпляри тієї ж задачі.
У функції "countDown" ми бачили самовиклик у дії, коли викликали "countDown" всередині самої функції.
Отже, підсумуємо. Рекурсія має три ключові характеристики:
базовий випадок, який описує, коли зупинитися;
крок рекурсії, який розбиває задачу на менші підзадачі;
самовиклик, який дозволяє функції викликати саму себе.
Розуміння і освоєння цих характеристик необхідне для того, щоб розуміти рекурсію і ефективно використовувати її в програмуванні.
Розуміння рекурсивних функцій
Пояснення механізму рекурсивних функцій на прикладі
Давайте розглянемо механізм рекурсивних функцій на прикладі обчислення факторіала числа.
Факторіал невід'ємного цілого числа , позначуваний як , є добутком усіх додатних цілих чисел, менших або рівних . Наприклад, (читається як "п'ять факторіал") дорівнює , що дорівнює .
Тепер давайте реалізуємо це за допомогою рекурсивної функції:
# Функція fact обчислює факторіал числа n def fact(n): if n == 0: return 1 return n * fact(n-1) # Основна частина програми. Читаємо вхідне значення n n = int(input()) # Обчислюємо та виводимо відповідь print(fact(n))
Тепер давайте зрозуміємо, як працює ця рекурсивна функція:
Базовий випадок:
У функції обчислення факторіала базовий випадок — це коли значення дорівнює . Ми знаємо, що факторіал дорівнює . Тому ми повертаємо .
Крок рекурсії:
Для будь-якого іншого значення (коли більше ), ми обчислюємо факторіал рекурсивно. Ми викликаємо функцію факторіала з аргументом та множимо результат на .
Це означає, що для обчислення нам спочатку потрібно обчислити , а потім помножити результат на . Цей процес триває до тих пір, поки ми не досягнемо базового випадку.
Давайте розглянемо приклад.
Якщо ми хочемо обчислити , то функція викличе , яка в свою чергу викличе і так далі, поки ми не досягнемо базового випадку.
Коли ми досягаємо базового випадку , тоді починаємо "розгортати" рекурсивні виклики.
Кожен рекурсивний виклик повертає свій результат і множить його на поточне значення .
У результаті факторіал обчислюється як , який далі обчислюється як і так далі, поки ми не отримаємо остаточний результат.
Отже, ось як працює рекурсія! Це схоже на зняття шарів з цибулі — шар за шаром — до тих пір, поки ми не дійдемо до середини. Розуміння цього рекурсивного процесу необхідне для вивчення рекурсивних функцій в програмуванні.
Продемонструйте пошагову роботу рекурсивних функцій, підкреслюючи важливість базового випадку
Тепер давайте крок за кроком розглянемо, як працюють рекурсивні функції, використовуючи послідовність Фібоначчі в якості прикладу. Послідовність Фібоначчі — це ряд чисел, в якому кожне число є сумою двох попередніх, зазвичай починаючи з та . Таким чином, послідовність виглядає наступним чином: і так далі.
Послідовність Фібоначчі визначається наступним чином:
Для заданого числа знайдіть значення -го елемента послідовності Фібоначчі.
Вхід. Одне натуральне число .
Вихід. Виведіть -ий елемент послідовності Фібоначчі.
2
1
5
5
Послідовність Фібоначчі має наступний вигляд:

Найбільше число Фібоначчі, що вміщується у типі int, дорівнює
Для достатньо використовувати тип даних int.
Нехай функція обчислює -те число Фібоначчі. Тоді маємо наступне рекурентне співвідношення:
Тепер давайте реалізуємо рекурсивну функцію для обчислення чисел Фібоначчі:
# Функція fib обчислює n-е число Фібоначчі def fib(n): if (n == 0): return 0 if (n == 1): return 1 return fib(n - 1) + fib(n - 2) # Основна частина програми. Читаємо вхідне значення n n = int(input()) # Обчислюємо та виводимо відповідь print(fib(n))
Тепер давайте крок за кроком розберемо, як працює ця рекурсивна функція:
Базовий випадок:
Базовий випадок відбувається, коли дорівнює або . У цих випадках ми вже знаємо числа Фібоначчі: і . Це найпростіший випадок, коли нам не потрібні додаткові обчислення.
Крок рекурсії:
Для будь-якого іншого значення (коли ) ми обчислюємо число Фібоначчі рекурсивно. Це відбувається шляхом сумування чисел Фібоначчі двох попередніх значень у послідовності ( і ).
Це означає, що для обчислення нам потрібно спочатку обчислити і , а потім додати ці результати. Цей процес триває доти, доки ми не досягнемо базового випадку.
Давайте розглянемо приклад.
Якщо ми хочемо обчислити , функція спочатку викличе та .
в свою чергу викличе та , а викличе та .
і є базовими випадками, тому вони повернуть та відповідно.
Як тільки ми отримаємо результати та , додасть їх разом .
аналогічним чином додасть результати та .
Нарешті, додасть та , і ми отримаємо результат .
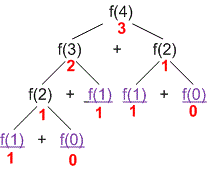
Цей покроковий процес демонструє, як працюють рекурсивні функції. Задача поступово розбивається на менші підзадачі, поки не будуть досягнуті базові випадки, а потім результати об'єднуються для вирішення початкової задачі. І, як ми бачили, базові випадки грають вирішальну роль у зупиненні рекурсії та забезпеченні вихідних точок для наших обчислень.
Обговоріть стек викликів та його використання при рекурсивних викликах функцій
Тепер давайте заглибимося в поняття стеку викликів та його використання при рекурсивних викликах функцій. Уявіть стек викликів як стопку тарілок у кафетерії. Коли Ви заходите до кафетерію, Ви берете тарілку і кладете її на верх стопки. Аналогічно, коли програма викликається функцією, інформація про цей виклик додається до стеку викликів.
Давайте розглянемо, як це працює з рекурсивними викликами функцій:
Виклики функцій та стек викликів:
Коли викликається функція, на вершині стеку викликів створюється новий фрейм для зберігання інформації про цей виклик. Цей фрейм включає параметри функції, локальні змінні та адресу повернення — точку в програмі, де має продовжитися виконання після завершення функції.
Кожен раз, коли відбувається виклик функції (будь то рекурсивний виклик чи звичайний виклик функції), новий фрейм додається на вершину стеку.
Рекурсивні виклики функцій:
У випадку рекурсивних викликів функція викликає саму себе всередині свого тіла. Це означає, що кожен рекурсивний виклик створює новий фрейм на вершині стеку викликів.
По мірі прогресування рекурсії до стеку викликів додаються все більше фреймів, і кожен з них представляє собою окремий екземпляр виклику функції.
Стек викликів відстежує всі ці виклики функцій, забезпечуючи тим самим, що програма знає, куди повернутися після завершення кожного виклику функції.
Базовий випадок і розгортання стеку:
Зрештою, по мірі прогресування рекурсії досягається базовий випадок. Це умова зупинки, яка запобігає безкінечному продовженню рекурсії.
Коли досягається базовий випадок, функція припиняє додаткові рекурсивні виклики і починає "розгортати" стек викликів.
Кожен фрейм знімається з вершини стеку викликів, і програма повертається до точки, де функція була спочатку викликана. Цей процес триває, поки весь стек викликів не буде повністю розгорнутий.
Питання пам'яті:
Важливо зазначити, що стек викликів має обмежений розмір, і надмірна рекурсія може призвести до помилки переповнення стеку, якщо стек стає занадто глибоким.
Тому при написанні рекурсивних функцій важливо переконатися, що існує коректний базовий випадок, щоб уникнути незкінченної рекурсії, і обмежити глибину рекурсії, щоб уникнути переповнення стеку.
Таким чином, стек викликів відіграє важливу роль у керуванні викликами функцій, включаючи рекурсивні виклики. Він відстежує послідовність викликів функцій і гарантує, що програма знає, куди повернутися після завершення кожного виклику функції. Розуміння стеку викликів є необхідним для розуміння роботи рекурсії і для написання ефективних і безпомилкових рекурсивних функцій.
Роз'яснити концепцію нескінченної рекурсії та способи її уникнення
Тепер давайте прояснимо концепцію нескінченної рекурсії та обговоримо, як її уникнути.
Нескінченна рекурсія:
Нескінченна рекурсія відбувається, коли рекурсивна функція викликає саму себе нескінченно, не досягаючи базового випадку, який би її зупинив.
Іншими словами, функція продовжує робити рекурсивні виклики, не просуваючись до базового випадку, що призводить до нескінченного циклу викликів функції.
Нескінченна рекурсія може швидко спожити всі доступні системні ресурси і викликати аварійне завершення програми або її зависання на невизначений час.
Як це відбувається:
Нескінченна рекурсія зазвичай виникає, коли в рекурсивній функції відсутній або неправильно вказаний базовий випадок.
Без базового випадку або з базовим випадком, який ніколи не досягається через неправильну логіку, функція буде викликати саму себе нескінченно.
Приклад:
Давайте розглянемо простий приклад рекурсивної функції для зворотного відліку від заданого числа:
def countDown(n): # Виведення поточного числа print(n) # Виклик функції countDown з на 1 меншим аргументом countDown(n - 1) # Приклад використання: countDown(5) # Виведення чисел з 5 до мінус нескінченності
У цій програмі немає базового випадку зупинки рекурсії, тому функція буде продовжувати кожен раз викликати себе з меншим значенням , що призводить до нескінченної рекурсії.
Як уникнути нескінченної рекурсії:
Щоб уникнути нескінченної рекурсії, важливо переконатися, що кожна рекурсивна функція має правильний базовий випадок.
Базовий випадок повинен представляти собою умову, при якій функція припиняє подальші рекурсивні виклики і повертає результат.
Під час написання рекурсивної функції завжди запитуйте себе: "Яка умова повинна змусити функцію зупинитися та повернути результат?"
Переконайтеся, що базовий випадок досяжний та що рекурсивні виклики ведуть до нього.
Виправлений приклад:
Давайте виправимо попередній приклад, додавши базовий випадок для зупинки рекурсії, коли досягає :
def countDown(n): # Базовий випадок if n == 0: return # Виведення поточного числа print(n) # Виклик функції countDown з на 1 меншим аргументом countDown(n - 1) # Приклад використання: countDown(5) # Виведення чисел з 5 до 1
Тепер функція припинить викликати саму себе, коли стане рівним . Це і стане запобіжником нескінченної рекурсії.
Отже, нескінченна рекурсія відбувається, коли рекурсивна функція викликає саму себе нескінченно, не досягаючи базового випадку. Щоб цього уникнути, завжди переконуйтесь, що ваші рекурсивні функції мають правильний базовий випадок, який зупиняє рекурсію та повертає результат. Тестування рекурсивних функцій з різними вхідними значеннями може допомогти виявити потенційні випадки нескінченної рекурсії під час розробки.
Реалізація рекурсивних алгоритмів
Представимо серію задач з програмування, придатних для рекурсії
Давайте обговоримо деякі відомі рекурсивні алгоритми.
Обчисліть значення виразу .
Вхід. Три натуральних числа .
Вихід. Виведіть одне число, яке дорівнює .
2 3 100
8
Задачу можна розв'язати зі складністю . Для цього достатньо написати наївний цикл for:
# Читаємо вхідні дані x, n, m = map(int,input().split()) # Ініціюємо змінну res значенням 1. # У цій змінній будемо обчислювати результат x^n mod m res = 1 # Обчислюємо значення x^n mod m використовуючи n операцій множення # 1 * x * x * ... * x for i in range(1,n+1): res = (res * x) % m # Виводимо відповідь print(res)
Така реалізація алгоритму перевищує Time Limit. Оскільки , а часовий ліміт для цієї задачі становить лише секунду, то ви не зможете виконати операцій за секунду, навіть використовуючи сучасні комп'ютери.
Як ми можемо прискорити процес множення? Наприклад, якщо ми хочемо обчислити , то можемо представити цей вираз у вигляді . Використовуючи лише одне множення для обчислення , ми можемо ефективно зменшити степінь удвічі: з до .
Наприклад, замість використання множень для знаходження , ми можемо переписати вираз наступним чином: , таким чином виконуючи всього множення. Аналогічно можна стверджувати, що для обчислення достатньо виконати лише множень.
Якщо показник степеня непарний, наприклад, , то значення обчислюємо як .
Наприклад, .
Ми підійшли до методу бінарного піднесення до степеня, техніки, яка використовується для ефективного обчислення великих степенів числа. Він заснований на принципі, що будь-яке число, піднесене до степеня, можна виразити як послідовність степенів двійки.
По заданим основі та показнику степеня , ми виражаємо як суму степенів двійки. Наприклад, якщо , ми можемо записати це як . Потім ми обчислюємо , перемножаючи разом значення , піднесені до кожної степені двійки, і об'єднуємо результати.
Припустимо, ми хочемо обчислити .
Виразимо у двійковій системі: у двійковому представленні.
Потім обчислимо , і (що відповідають встановленим бітам у двійковому представленні ).
Нарешті, перемножимо ці значення: .
Переваги. Бінарне піднесення до степеня скорочує кількість необхідних множень порівняно з наївним піднесенням до степеня. Воно особливо ефективне для великих степенів, оскільки вимагає всього множень замість множень.
Щоб знайти значення , ми будемо використовувати формулу:
# Функція myPow обчислює значення x^n mod m def myPow(x, n, m): if (n == 0): return 1 if (n % 2 == 0): return myPow((x * x) % m, n / 2, m) return (x * myPow(x, n - 1, m)) % m # Основна частина програми. Читаємо вхідні дані x, n, m = map(int, input().split()) # Обчислюємо та виводимо відповідь print(myPow(x, n, m))
Python має вмонтовану функцію , яка обчислює . Попередній код можна переписати наступним чином:
# Читаємо вхідні дані x, n, m = map(int, input().split()) # Обчислюємо та виводимо відповідь print(pow(x, n, m))
Знайдіть НСД (найбільший спільний дільник) двох натуральних чисел.
Вхід. Два натуральних числа та .
Вихід. Виведіть НСД чисел та .
42 24
6
Найбільший спільний дільник (НСД) двох цілих чисел і — це найбільше додатне число, яке ділить і , і без залишку.
Приклад:
Розглянемо два числа та .
Дільниками числа будуть і .
Дільниками числа будуть і .
Спільними дільниками чисел та будуть і .
З цих дільників найбільшим буде .
Тому .
Властивості:
НСД є завжди невід'ємним цілим числом.
Якщо та обидва нулі, то .
Якщо або (або обидва) від'ємні, то дорівнює НСД їх абсолютних значень.
Якщо або дорівнює нулю, то дорівнює абсолютному значенню ненульового цілого числа.
НСД будь-якого числа та дорівнює абсолютному значенню цього числа.
Застосування:
НСД використовується в різних математичних обчисленнях, включаючи спрощення дробів та знаходження найменшого спільного знаменника.
НСД використовується в криптографічних алгоритмах, таких як RSA, для генерації ключів і шифрування.
НСД також використовується в алгоритмах інформатики, таких як алгоритм Евкліда для ефективного обчислення.
Алгоритм Евкліда — це ефективний метод знаходження НСД двох цілих чисел. Він заснований на принципі, що НСД двох чисел залишається незмінним, якщо ми будемо віднімати менше число від більшого до тих пір, поки одне з них не стане рівним нулю.

Якщо замість операції "мінус" використовувати операцію "mod", то обчислення будуть проходити швидше.
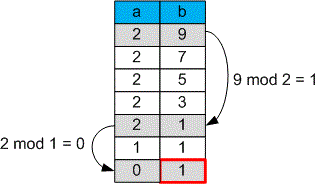
Наприклад, щоб обчислити за допомогою віднімання, знадобиться виконати операцій. Однак при використанні операції взяття остачі достатньо лише однієї дії.
Для двох цілих чисел та , де , ми повторюємо наступні кроки:
Якщо дорівнює нулю, то НСД дорівнює .
У протилежному випадку ми замінюємо на , а на залишок від ділення на . Це можна виразити як та .
Ми продовжуємо цей процес, доки не стане рівним нулю.
НСД та — це значення , коли стає рівним нулю.
Алгоритм Євкліда є ефективним, з часовою складністю . Він завжди завершується, оскільки значення зменшується з кожною ітерацією і в кінці стає рівним нулю.
НСД двох чисел можна обчислити за допомогою наступної формули:
def gcd(a, b): if a == 0: return b if b == 0: return a if a > b: return gcd(a % b, b) return gcd(a, b % a) # Основна частина програми. Читаємо вхідні дані. a, b = map(int, input().split()) # Обчислюємо та виводимо НСД двох чисел. print(gcd(a, b))
Дану формулу можна виразити в іншій формі:
def gcd(a, b): if b == 0: return a return gcd(b, a % b) # Основна частина програми. Читаємо вхідні дані. a, b = map(int, input().split()) # Обчислюємо та виводимо НСД двох чисел. print(gcd(a, b))
Python має вбудовану функцію , яка обчислює найбільший спільний дільник двох чисел. Попередній код можна переписати наступним чином:
import math # Читаємо вхідні дані. a, b = map(int, input().split()) # Обчислюємо та виводимо НСД двох чисел. print(math.gcd(a, b))
Список задач
Рекурсивні програми:
1658. Факторіал (використано в лекції)
Числа Фібоначчі:
3258. Послідовність Фібоначчі (використано в лекції)
НСД / НСК:
1601. НСД двох чисел (використано в лекції)
Біноміальний коефіцієнт:
Піднесення до степеня:
