Періодичні точки
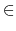
Обчислення кількості фіксованих точок і, загалом, кількості періодичних орбіт у динамічній системі є питанням, яке привертає інтерес з різних галузей досліджень. Однак динаміка може виявитися дуже складною для опису, навіть у, здавалося б, простих моделях. У цьому завданні вам буде запропоновано обчислити кількість періодичних точок періоду n кусочно-лінійного відображення f, яке відображає дійсний інтервал [0, m] у себе. Тобто, маючи відображення f : [0, m] → [0, m], ви повинні обчислити кількість розв'язків рівняння f^n(x) = x для x [0, m], де f^n є результатом ітерації функції f загалом n разів, тобто

де позначає композицію відображень, (gh)(x) = g(h(x)).
На щастя, відображення, з якими вам доведеться працювати, задовольняють деякі особливі властивості:
m буде додатним цілим числом, і образ кожного цілого числа в [0, m] під f знову є цілим числом у [0, m], тобто для кожного k {0, 1,..., m} ми маємо, що f (k) {0, 1,..., m}.
Для кожного k {0, 1,..., m - 1}, відображення f є лінійним на інтервалі [k, k + 1]. Це означає, що для кожного x [k, k + 1], його образ задовольняє f (x) = (k + 1 - x)f (k) + (x - k)f (k + 1), що еквівалентно тому, що його графік на [k, k + 1] є прямолінійним відрізком.

Рисунок 1: Графіки третього відображення у вхідному прикладі, f_3 (ліворуч), та його квадрата, f_3^2 (праворуч).
Оскільки може бути багато періодичних точок, вам доведеться вивести результат за модулем цілого числа.
Вхідні дані
Вхід складається з кількох тестових випадків, розділених одним порожнім рядком. Кожен тестовий випадок починається з рядка, що містить ціле число m (1 ≤ m ≤ 80). Наступний рядок описує відображення f; він містить m+1 цілих чисел f(0), f(1), ..., f(m), кожне з яких знаходиться між 0 та m включно. Тестовий випадок закінчується рядком, що містить два цілі числа, розділені пробілом, n (1 ≤ n ≤ 5 000) та модуль, що використовується для обчислення результату, "mod" (2 ≤ mod ≤ 10 000).
Вхід закінчується рядком, що містить '0'.
Вихідні дані
Для кожного випадку ваша програма повинна вивести кількість розв'язків рівняння f^n(x) = x у інтервалі [0, m] за модулем "mod". Якщо існує нескінченно багато розв'язків, виведіть 'Infinity'.