Two pointers technique
The Two Pointers technique is a strategy commonly used in computer science and programming for solving problems involving arrays or sequences. It involves using two pointers that traverse the array or sequence from different positions, often moving in opposite directions or at different speeds. This technique is particularly useful for solving problems related to searching, optimization, or manipulation of arrays efficiently.

Here's a breakdown of how the Two Pointers technique works:
Initialization: Initially, you set up two pointers, usually at different positions within the array or sequence.
Movement: You iteratively move the pointers based on certain conditions until they meet or reach a specific condition. The movement of pointers can be controlled based on the problem requirements. For example, one pointer might move faster than the other, or they might move in opposite directions.
Condition Checking: At each step of iteration, you check certain conditions based on the problem requirements. These conditions often determine whether to move the pointers, update some variables, or perform other operations.
Termination: The process continues until one or both pointers reach the end of the array or sequence, or until some other termination condition is met.
The Two Pointers technique is especially useful in problems that involve searching for pairs or subarrays that meet specific criteria, finding optimal solutions, or manipulating sequences efficiently without using nested loops. It often provides a more efficient solution compared to brute-force approaches, especially for problems with linear or logarithmic time complexity requirements.
Store the numbers in a linear array. Then print them in reverse order.
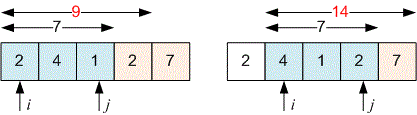
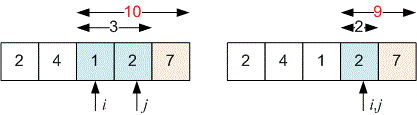
Let’s consider a solution for reversing an array using the two-pointer technique.
Set two variables and (we'll call them pointers):
at the beginning of the array ;
at the end of the array ;
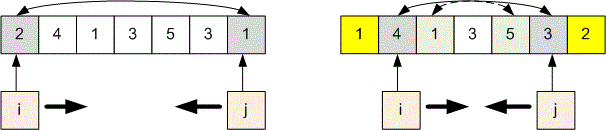
Next, start a while loop, in which:
the values of and are swapped;
then is incremented by , and is decremented by ;
We continue the loop until the pointers and meet.
Note that the values of and can be swapped using an additional variable by performing three operations:

Declare an array.
#define MAX 110 int m[MAX];
Read the input data.
scanf("%d",&n);
for(i = 1; i <= n; i++)
scanf("%d",&m[i]);Reverse the array using the two-pointer technique.
i = 1; j = n;
while(i < j)
{
temp = m[i]; m[i] = m[j]; m[j] = temp;
i++; j--;
}Print the numbers.
for(i = 1; i <= n; i++)
printf("%d ",m[i]);
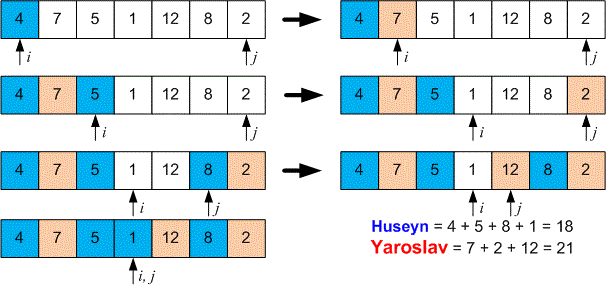
printf("\n");Huseyn and Yaroslav are playing a card game. There are n cards laid out in a row on the table, each with a different number written on it. The players take turns. Huseyn starts the game. On each turn, a player can take either the leftmost or the rightmost card. The player will always choose the card with the highest number. The game ends when there are no cards left on the table. Find the sum of the numbers on the cards collected by Huseyn and Yaroslav at the end of the game.
Input. The first line contains the number of cards on the table. The second line contains positive integers, each indicating the number on a card. All numbers are not greater than .
Output. Print the sum of the numbers on the cards collected by Huseyn and Yaroslav at the end of the game.
7 4 7 5 1 12 8 2
18 21
Let the array contain the numbers written on the cards. We initialize pointers at the beginning of the array and at the end of the array.

On each turn, a player takes the card with the maximum value , after which the card is removed from the table (perform the operation if the card is chosen, and if the card is chosen). For each player, we keep track of the sum of the selected cards in two variables. The process continues until all cards are removed from the table, that is, until the pointers and meet.
Example
The game will proceed as follows.
Declare the arrays. The sum of the numbers on the cards collected by Huseyn and Yaroslav will be stored in and , respectively.
int m[10001], res[2];
Read the input data.
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%d", &m[i]);Set the pointers and .
i = 0; j = n - 1;
The players take turns, making moves in total. Huseyn takes turns for even , and Yaroslav takes turns for odd . Accordingly, Huseyn's sum will accumulate in , and Yaroslav's sum will accumulate in .
for (k = 0; k < n; k++)
{On each turn, the player chooses the card with the maximum value .
if (m[i] > m[j])
res[k % 2] += m[i++];
else
res[k % 2] += m[j--]; ;
}Print the answer.
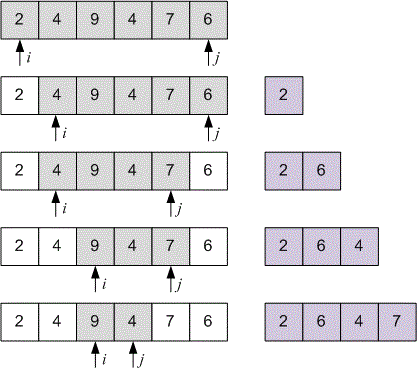
printf("%d %d\n", res[0], res[1]);Huseyn arranged cards in a row with numbers . Then he collected them and rearranged them in a different order: . This is the sequence he gave to Yaroslav. Your task is to help Yaroslav restore Hussein's original sequence.
For example, if Yaroslav received the sequence , then he should return the sequence to Huseyn.
Input. The first line contains one integer , representing the number of cards. The second line contains positive integers written on the cards. All numbers are no greater than .
Output. Print Huseyn's original sequence.
6 2 4 9 4 7 6
2 6 4 7 9 4
7 5 7 34 1 89 4 2
5 2 7 4 34 89 1
Let the array contain the numbers written on the cards. Initialize two pointers: at the beginning of the array and at its end.

To restore the original sequence, alternately take cards from the left and the right until all elements have been processed. With each selection, the corresponding pointer changes its position: moves to the right, moves to the left.
Example
Let’s consider a few steps of the algorithm using the first test case as an example.
Declare an array.
int a[100001];
Read the input data.
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%d", &a[i]);Set the pointers and .
i = 0; j = n - 1;
While the inequality holds, alternately print and , simultaneously moving the pointers.
while (i <= j)
{
printf("%d ", a[i++]);
if (i > j) break;
printf("%d ", a[j--]);
}Huseyn has a string consisting of characters and . To entertain himself, he came up with the following game. Huseyn can perform one of two operations on the string:
append to the left end, and to the right end;
append to the right end, and to the left end;
For example, from the string , Huseyn can obtain or .
You are given a string obtained after all of Huseyn's operations (it is possible that he did not perform any operation). Determine the smallest possible length the string could have initially had.
Input. A single string of length no more than , consisting only of characters and .
Output. Print the smallest possible length of the string that Huseyn could have initially had.
01010010
8
1001110
1
Let's consider the input string — the resulting string after Huseyn has performed all operations. Initialize two pointers: at the start of the string and at the end.
If , then the characters at the ends of the string are different: either on the left and on the right, or on the left and on the right. This means the previous string could have been extended by applying one of the specified operations. In this case, move both pointers and one position towards each other and check again whether the substring could have been obtained through Huseyn's operations.
As soon as the current substring satisfies , it can no longer be produced by the given operations. Print its length — this is the original string that Huseyn had.
Example
Let's perform Huseyn's operations in reverse order.
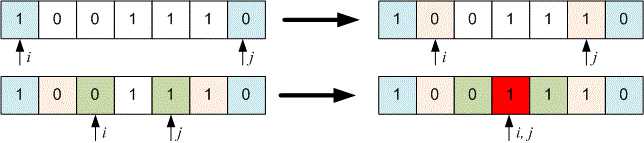
The string was originally the one Huseyn had.
Read the input string and calculate its length, storing it in the variable .
cin >> s; res = s.size();
Initialize two pointers: at the start and at the end of the string.
i = 0; j = s.size() - 1;
If , then the characters at the ends of the string are different. Huseyn could have obtained the substring from the substring .
while ((i < j) && (s[i] != s[j]))
{Move both pointers and one position towards each other and decrease the current size of the substring .
i++; j--; res -= 2; }
Print the answer.
cout << res << endl;
Given an array , sorted in ascending order and containing integers. Determine whether there exists a pair of numbers , where , such that their sum is equal to .
Input. The first line contains two integers and . The second line contains non-negative integers, each of which is not greater than .
Output. Print "YES" if such a pair of elements exists, and "NO" otherwise.
10 13 1 3 5 6 8 10 11 11 11 16
YES
8 61 5 5 8 12 16 21 44 50
NO
Let be the input array of numbers. Initialize pointers to the beginning of the array and to the end of the array. The array is already sorted according to the problem conditions.
While pointers and do not meet, perform the following actions:
If , then the desired pair of elements is found. Print it and terminate the program.
If , then move pointer one position to the right. In this case, the sum will increase;
If , then move pointer one position to the left. In this case, the will decrease;
Example
Let’s consider the first test. Initialize the pointers. Simulate the algorithm’s operation. The value of , we are looking for two numbers with a sum of .

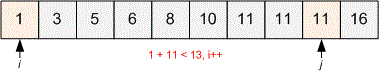


Read the input data.
scanf("%d %d", &n, &x);
v.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &v[i]);Initialize the pointers.
int i = 0, j = v.size() - 1;
Move pointer forward and pointer backward.
while (i < j)
{If , then the desired pair of elements is found. Print it and terminate the program.
if (v[i] + v[j] == x)
{
printf("YES\n");
return 0;
}If , then move pointer one position to the right;
If , then move pointer one position to the left;
if (v[i] + v[j] < x) i++; else j--; }
If the desired pair is not found, print "NO".
printf("NO\n");Given an array of integers and an integer . Find a triplet of numbers in the array whose sum equals . All indices should be different.
Input. The first line contains the size of the array and the value of . The second line contains integers, each of which does not exceed in absolute value.
Output. If the required triplet exists, print it in any order. If multiple triplets exist, print any one of them. If the desired triplet does not exist, print .
8 19 20 3 5 1 15 7 17 12
1 3 15
Let be an input array. Iterate through all possible indices . Then, for each value of , find a pair of indices such that and . This can be achieved on a sorted array using the two-pointer technique in linear time.

Read the input data.
cin >> n >> x; v.resize(n); for (i = 0; i < n; i++) cin >> v[i];
Sort the input array.
sort(v.begin(), v.end());
Iterate through the values .
for (k = 0; k < n - 2; k++)
{Find a pair of indices such that and . Initialize the indices and .
i = k + 1; j = n - 1; s = x - v[k];
Use the two-pointer technique to find the desired pair .
while (i < j)
{
if (v[i] + v[j] == s)
{If the pair is found, print the desired triplet of numbers .
printf("%d %d %d\n", v[k], v[i], v[j]);
return 0;
}If , then move pointer one position to the right;
If , then move pointer one position to the left;
if (v[i] + v[j] < s) i++; else j--; } }
If the triplet of numbers is not found, print .
cout << -1 << endl;
Given a sorted array of integers. For each index , find the number of elements in the array that lie between and inclusive.
Input. The first line contains the size of array . The second line contains integers, each ranging from to , in sorted order.
Output. Print integers. For each index of the array, print the number of elements lying between and inclusive.
10 1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 5 4 3 2 1
The interval will be called good if the numbers in it lie in the range inclusive (meaning ).
We implement a sliding window using two pointers and and maintain it so that the current interval is good, while the interval is bad.
For example, for the following sequence:
the intervals , and are good.
the intervals are bad.
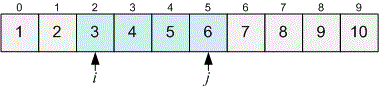
If , extend the current interval to . Otherwise, reduce it to . Before moving the pointer , print the number of elements lying between and inclusive. It equals .
The algorithm’s complexity is linear, i.e. .
Example
Let’s consider the movement of pointers for the given example.
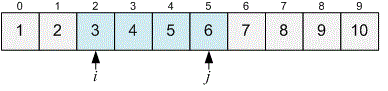
For the given condition , so we move the pointer forward.
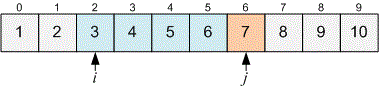
Now . We need to move the pointer forward. However, before moving it, print the number of elements lying between and inclusive. It is equal to .

Move forward until .

Now . Print the answer for (it equals ) and increase by .
Read the input data.
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%d", &a[i]);Initialize the pointers .
i = j = 0;
Move the pointers forward until an answer is found for each value of .
while (i < n) // [i..j]
{If (and has not exceeded the array bounds, meaning ), extend the current interval by incrementing the pointer .
if ((j < n) && (a[j] <= 2 * a[i])) j++;
else
{If , print the answer for index and increment by one.
printf("%d ", j - i);
i++;
}
}Along the beautiful Adriatic coast, there are hotels. Each hotel has its cost in euros. Petr won euros in the lottery. Now he wants to buy a sequence of consecutive hotels one after another so that the sum of the costs of these consecutive hotels is as large as possible, but does not exceed .
You need to calculate this maximum possible total cost.
Input. The first line contains two integers and . The next line contains positive integers less than , representing the costs of the hotels in the order they are located along the coast.
Output. Print the desired maximum cost (it will be greater than in all tests).
5 12 2 1 3 4 5
12
Store the hotel costs in the array. We’ll call the interval good if the sum of hotel costs within it does not exceed .
Let’s implement a sliding window using two indices and , and maintain it so that the current interval is good. Let be the sum of hotel costs within the interval . If , then expand the current interval to . Otherwise, shrink it to . Find the maximum among the costs of all considered good intervals.
Example
Consider the movement of pointers for the given example.
When moves forward until the sum of numbers in the interval does not exceed . Stop at the interval because the sum there is equal to , while the sum in the interval is equal to .
When , we cannot move forward because the sum in the interval is equal to .
When move forward to the interval .

The maximum value among all good intervals is equal to and is achieved in the interval .
Read the input data.
scanf("%d %lld", &n, &m);Initialize the variables:
in , the maximum value among the costs of all processed good intervals is computed;
in , the sum of numbers in the current interval is maintained. All the numbers in the current interval are stored in the queue ;
s = res = 0;
Process the hotel costs sequentially.
for (i = 0; i < n; i++)
{Read and add the cost of the current hotel to the queue.
scanf("%d", &val);
q.push(val);Update the sum within the interval. All elements of the current interval are stored in the queue .
s += val;
If the sum of numbers in the current interval exceeds , we remove elements from the beginning of the interval.
while (s > m)
{
s -= q.front();
q.pop();
}Compute the maximum value among the sums of elements in good intervals (where the cost of hotels does not exceed ).
if (s > res) res = s; }
Print the answer.
printf("%lld\n", res);Given an array of positive integers, find the number of subarrays whose sum is equal to .
Input. The first line contains the size of the array and the target sum . The next line contains integers — the contents of the array.
Output. Print the required number of subarrays.
5 7 2 4 1 2 7
3
Let's implement a sliding window using two pointers, and . For each fixed , expand the interval as much as possible so that the sum of its elements does not exceed . In other words, for each , search for the largest possible such that the sum of elements in the interval does not exceed , while the sum of elements in the interval exceeds .
Let be the sum of numbers in the interval . If , expand the interval to . Otherwise, shrink it to . Count the number of intervals with a sum of .
Example
Let's examine the movement of the pointers for the given example.
, moves forward until the sum of the numbers in the interval exceeds . We stop at the interval , since the sum of the numbers in it is , while in the interval , the sum of the numbers is already .
, moves forward to . The sum of the numbers in the interval is , while in the interval , it is already .
, the considered interval is . The sum of the numbers in it is , but we cannot move the index forward because the sum of the numbers in the interval is , which is greater than .
, the considered interval is . The sum of the numbers in it is , but we cannot move the index forward because the sum of the numbers in the interval is , which is greater than .
, the considered interval is . The sum of the numbers in it is .
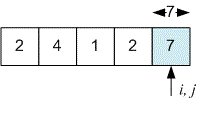
The number of subarrays with a sum of is . They start at indices , and .
Declare an array.
#define MAX 200001 long long a[MAX];
Read the input data.
scanf("%d %lld", &n, &x);
for (i = 0; i < n; i++)
scanf("%lld", &a[i]);Initially, set the current interval . The sum of the numbers in this interval is .
s = j = 0;
For each value of , sequentially process the intervals .
for (i = 0; i < n; i++)
{For the fixed left end of the interval , search for the largest such that the sum of elements in this interval does not exceed .
while ((j < n) && (s + a[j] <= x)) s += a[j++];
If the sum of the numbers in the current interval equals , increase the desired subarray count by .
if (s == x) cnt++;
Recompute the sum for the interval .
s -= a[i]; }
Print the answer.
printf("%lld\n", cnt);Ziya will take part in the sequence competition tomorrow. The number is called the top of some sequence if the sequence is a subsequence of this sequence. The strength of each sequence is considered to be its largest vertex.
Tomorrow all students will go to the competition and the winner of the strongest sequence will be the winner. Zia has the sequence . He wants to take over the competition scoring system and remove sequences from it with more force than himself. However, Zia does not know the power of his own consistency, but really wants to win. Help him calculate the strength of his own sequence.
Input. The first line contains the number of numbers in Zia's sequence. The next line contains integers — the elements of the sequence.
Output. Print one number — the strength of the given sequence.
2 2 10
0
3 1 2 3
1
5 1 10 2 3 1
2
Let be the input array of numbers. Initialize the pointers at the beginning of the array and at the end of the array. We will count the strength of the sequence in the variable . Initially, set .
While the pointers and do not meet, perform the following actions:
Move the pointer one position to the right if it does not point to the number .
Move the pointer one position to the left if it does not point to the number .
If both pointers point to the number , increase by one and move each pointer one position in the corresponding direction.
After the algorithm completes, the answer will be the value .
Example
Consider the second test. Initialize the pointers. Move the pointer to the right and the pointer to the left until they both point to the number .
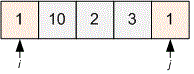
Move the pointer to the right and the pointer to the left until they both point to the number .

The pointers meet, we stop the algorithm. The answer will be the value .
Read the input data.
scanf("%d", &n);
v.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &v[i]);Set the pointers to the start and end of the array .
int i = 0, j = v.size() - 1;
In the variable , we count the strength of the sequence.
k = 1;
while (i <= j)
{Move the pointer to the right until it encounters the number .
if (v[i] != k) i++;
Move the pointer to the left until it encounters the number .
if (v[j] != k) j--;
If both pointers point to the number , then increase by one.
if (v[i] == k && v[j] == k) k++; }
Print the answer.
printf("%d\n", k - 1);Today, programmers have gathered. Each programmer has a rating that reflects his strength. The rating is an integer between and . Your rating as a programmer is . From all the programmers gathered today, you want to choose two for your team. They must be selected in such a way that their total rating is maximized but does not exceed your rating, as you want to be the leader of this team.
Input. The first line contains two integers: — the number of programmers, and — your rating. The second line contains integers — the ratings of the programmers.
Output. Print a single integer — the maximum sum of the ratings of the selected programmers, or if it is impossible to find such two people.
5 8 5 3 4 6 5
8
7 19 8 4 25 1 20 5 12
17
4 76 38 41 39 40
-1
Sort the programmers' ratings in the array . To find two programmers with the maximum total rating, we'll use the two-pointer technique.
Initialize the pointer at the beginning of the array and the pointer at the end of the array.
Among all possible sums , not exceeding , find the maximum. If , move the pointer forward. Otherwise, move the pointer backward. Continue this process until the pointers meet.
Example
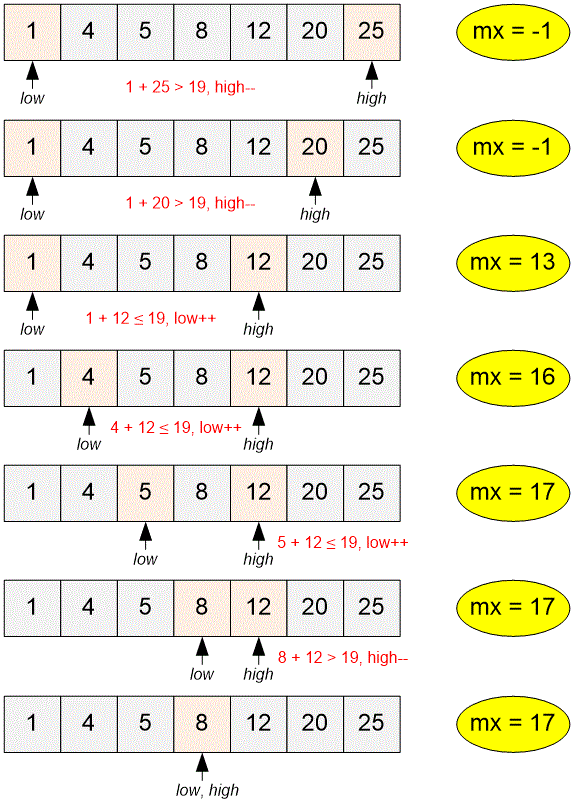
Let's consider the second test. Sort the numbers and initialize the pointers. Simulate the algorithm's execution. In this case, : we are looking for two numbers with the maximum sum that does not exceed .
Read the input data.
scanf("%d %d", &n, &m);
v.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &v[i]);Sort the programmers’ ratings.
sort(v.begin(), v.end());
Initialize the pointers. The variable stores the maximum sum of two elements.
int mx = -1, low = 0, high = n - 1;
The pointer is moved forward, and the pointer is moved backward.
while (low < high)
{Among all possible sums that do not exceed find the maximum. If , move forward. Otherwise, move backward.
if (v[low] + v[high] <= m)
{
mx = max(mx, v[low] + v[high]);
low++;
}
else high--;
}Print the answer.
printf("%d\n", mx);Bessie the cow, always a fan of shiny objects, has taken up a hobby of mining diamonds in her spare time! She has collected diamonds of varying sizes, and she wants to arrange some of them in a display case in the barn.
Since Bessie wants the diamonds in the case to be relatively similar in size, she decides that she will not include two diamonds in the case if their sizes differ by more than (two diamonds can be displayed together in the case if their sizes differ by exactly ). Given , help Bessie determine the maximum number of diamonds she can display in the case.
Input. The first line contains and . The next lines each contain an integer giving the size of one of the diamonds. All sizes will be positive and will not exceed .
Output. Print the maximum number of diamonds that Bessie can showcase.
5 3 1 6 4 3 1
4
Sort the array of diamond sizes. For each index , consider the sequence such that , but at the same time, . Among all such sequences, find the one that contains the largest number of elements.
Example
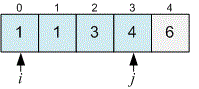
Sort the sizes of the diamonds.
Consider the interval . The difference between the sizes of the diamonds in this interval does not exceed . However, Bessie will not be able to showcase all the diamonds in the interval in the barn, since .
Declare an array to store the sizes of the diamonds.
int m[1000];
Read the input data.
scanf("%d %d", &n, &k);
for (i = 0; i < n; i++)
scanf("%d", &m[i]);Sort the array.
sort(m, m + n);
The maximum number of diamonds that Bessie can display in the barn is counted in the variable .
res = 0;
For each index , consider the sequence of the greatest length such that . Count the length of this sequence in the variable .
for (i = 0; i < n; i++)
{
cnt = 0;
for (j = i; j < n; j++)
{As soon as the condition becomes true, exit the loop.
if (m[j] > m[i] + k) break;
cnt++;
}Among the lengths of all sequences, find the maximum.
if (cnt > res) res = cnt; }
Print the answer.
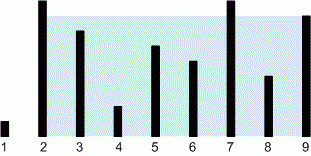
printf("%d\n", res);There is an array of integers of length , representing the heights of vertical lines. For each -th line, its endpoints are defined by the coordinates and .
Find two lines that, together with the -axis, form a container capable of holding the maximum amount of water.
Input. The first line contains the size of the array . The second line contains positive integers, the elements of the array , each of which does not exceed .
Output. Print the maximum volume of water that the container can hold.
9 1 8 6 2 5 4 8 3 7
49
First, compute the volume of water in the container formed by the outermost vertical lines, i.e., between the lines of the pair . Then, move the pointers and towards each other:
if , increase by ;
if , decrease by ;
The volume of water between the lines and is equal to . Among all the calculated values, find the maximum.
The problem can be solved in . However, due to the constraint , such a solution would result in a time limit exceeded (TLE). It is sufficient to iterate over the pairs of lines , where , and for each such pair, calculate the volume of water they can hold. Among all the computed values, find the maximum volume.
Example
The container from the first test looks like this:
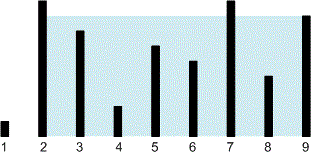
The maximum amount of water can be held between the lines and . The water level height is , and the volume of water is .
Read the input data.
scanf("%d", &n);
h.resize(n);
for (i = 0; i < n; i++)
scanf("%lld", &h[i]);Store the maximum amount of water the container can hold in the variable .
long long res = 0;
Initialize two pointers .
int l = 0, r = h.size() - 1;
Move the pointers and towards each other until they meet.
while (l < r)
{The volume of water between the lines and is equal to . Among all such volumes, find the maximum.
res = max(res, min(h[l], h[r]) * (r - l));
Move the pointers.
if (h[l] < h[r])
l += 1;
else
r -= 1;
}Print the answer.
printf("%lld\n", res);You are given a list of songs that played on Radio 106 FM. The list contains a total of songs. Find the length of the longest fragment of the list that consists of non-repeating songs.
Input. The first line contains the number of songs in the list. The second line contains integers , which are the identification numbers of the songs.
Output. Print the length of the longest fragment of the list that consists of unique songs.
8 1 2 1 3 2 7 4 2
5
4 1 1 2 1
2
Let the array store the identification numbers of the songs. Using two pointers, we will maintain a sliding window in which the songs do not repeat. In other words, all the songs in the segment are unique. The songs from this segment will be stored in a set . For each value of , we will try to extend the segment to the maximum possible length. That is, for a fixed , we will search for such a that in the segment the songs do not repeat, but in the segment duplicates already appear.
When processing the current song at index , there are two possible cases:
If the song is not present in the segment , add it to this segment, extending it to ;
If the song is already present in the segment, shift the left boundary to the right until disappears from the segment . Then, add to the segment, extending it to . With each shift of , remove the corresponding elements from the set ;
Among all possible segments with unique songs, find the maximum length. This will be the answer to the problem.
Example
Let’s consider how the segments with unique songs will change for the first example.
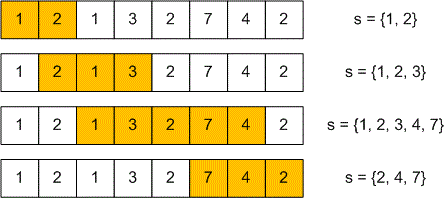
The length of the longest segment is .
Read the input data. The identification numbers of the songs are stored in the array .
scanf("%d", &n);
v.resize(n);
for (i = 0; i < n; i++)
scanf("%d", &v[i]);Maintain the segment of unique songs (i.e., the songs from to do not repeat). In the set , store the identification numbers of the songs from this segment. The variable tracks the length of the longest fragment with unique songs.
i = res = 0;
for (j = 0; j < n; j++)
{Consider the current song at index . If it is already in the set , it will not be possible to extend the current segment by including the -th song. In this case, we need to shift the left boundary , removing the song from the set , until the -th song disappears from the set .
while (s.find(v[j]) != s.end())
{
s.erase(v[i]);
i++;
}Add the -th song to the segment and, accordingly, to the set . Thus, the segment will not contain any repeated songs.
s.insert(v[j]);
Among all possible segments , find the longest one. The length of the segment is .
res = max(res, j - i + 1); }
Print the answer.
printf("%d\n", res);