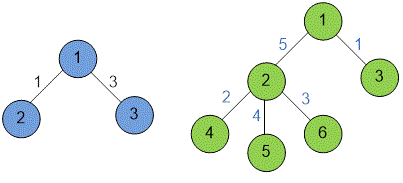
Trees
Trees are one of the key data structures in algorithms and appear in a wide range of problems.
A tree is a connected, acyclic, undirected graph.
A graph is called a tree if it satisfies the following properties:
Connected — there is a path between every pair of vertices in the graph.
Acyclic — the graph contains no cycles.
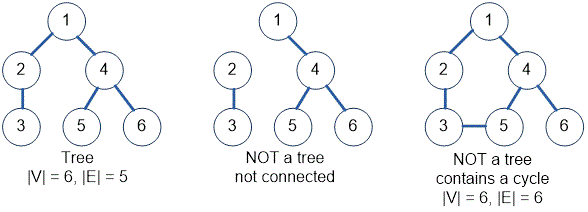
In a tree with vertices, there are always exactly edges.
Fundamental Properties of a Tree
1. Connectivity and Uniqueness of Paths
In a tree, there is a unique path between any pair of vertices.
2. Number of Edges
For any tree:
3. No Cycles
Adding even a single edge to a tree always creates a cycle.
4. Root (for a rooted tree)
If one vertex is chosen as the root, the tree becomes directed from the root to its descendants. This is used in recursive traversals and algorithms (, , etc.).
5. Subtrees
Any vertex along with its descendants forms a subtree. A subtree is itself a tree.
6. Leaves
Vertices with zero children (in a rooted tree) are called leaves.
7. Depth and Height
Depth of a vertex is the distance from the root to that vertex.
Height of a tree is the maximum depth among all vertices.
8. Center of a Tree
The center is the vertex (or a pair of adjacent vertices) that minimizes the maximum distance to all other vertices.
Alternative Definitions of a Tree
The following definitions of a tree are equivalent and can be used in different contexts:
A cycle-free graph that becomes disconnected if any edge is removed.
A connected graph with vertices and edges.
An acyclic graph with edges and exactly one connected component.
Representing Trees in Code
Depending on the problem and the type of tree (general, binary, rooted, etc.), different data structures are used:
1. Adjacency Lists
This approach is often used in competitive programming problems and when working with undirected or directed trees.
int n; vector<vector<int>> tree(n); // tree with n vertices // adding an edge between vertices u and v tree[u].push_back(v); tree[v].push_back(u); // for an undirected tree
2. Parent Array
A very compact representation, especially useful when the tree is already constructed.
vector<int> parent(n); // parent[i] --- he parent of vertex i // if i is the root, parent[i] is usually set to -1 or 0
3. Pointers / Structures (OOP Style)
Commonly used when constructing binary trees, tries, decorators, especially in Python/Java/C++ with object-oriented programming.
Binary Tree:
struct Node
{
int val;
Node* left;
Node* right;
Node(int v) : val(v), left(nullptr), right(nullptr) {}
};General Tree:
struct Node
{
int val;
vector<Node*> children;
Node(int v) : val(v) {}
};A graph with vertices is a tree if and only if:
The graph is connected. Start a depth-first search from the first vertex. Count the number of visited vertices during the search. If it equals , then the graph is connected.
. If the graph is a tree, then it contains edges
The graph does not contain cycles. Start a depth-first search from the first vertex. If a back edge exists, then the graph has a cycle and is not a tree.
Satisfying conditions and or and is sufficient for the graph to be a tree.
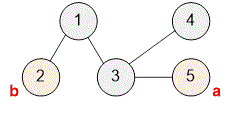
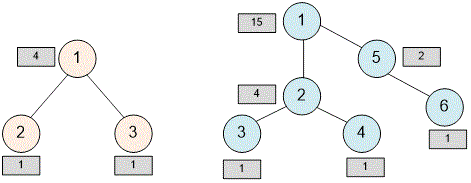
Example
The graph provided in the example is a tree.
Declare the adjacency matrix of the graph and the array .
#define MAX 110 int g[MAX][MAX], used[MAX];
The dfs function performs a depth-first search starting from vertex . The parent of vertex is . If a cycle is detected, the variable is set to .
void dfs(int v, int p)
{If the graph is no longer a tree , there is no need to continue the search.
if (flag) return;
Mark the vertex as visited.
used[v] = 1;
The vertex is visited, increase by .
c++;
The edge will be a back edge and form a cycle if and vertex is already visited . If a cycle is detected, set . If no cycle is detected, continue the search from vertex .
for(int i = 0; i < n; i++)
if ((i != p) && g[v][i])
if(used[i]) flag = 1; else dfs(i,v);
}The main part of the program. Read the input data.
scanf("%d",&n);
for(i = 0; i < n; i++)
for(j = 0; j < n; j++)
scanf("%d",&g[i][j]);Count the number of visited vertices during the depth-first search in the variable . Set if there is no cycle in the graph. If a cycle is detected, becomes .
c = 0; flag = 0;
All vertices are initially unvisited (initialize the array with zeroes).
memset(used,0,sizeof(used));
Start the depth-first search from vertex . Since it is the root of the tree, it has no parent. Pass the value as the second argument to the dfs function.
dfs(0,-1);
The graph is not a tree if there is a back edge or if the graph is not connected .
if (flag || (c != n)) printf("NO\n"); else printf("YES\n");Python implementation — checking the conditions 1) and 3)
The dfs function performs a depth-first search starting from vertex . The parent of vertex is . If a cycle is detected, the variable is set to .
def dfs(v, p):
Declare the global variables used by the function.
global flag, c
If the graph is no longer a tree , there is no need to continue the search.
if flag: return
Mark the vertex as visited.
used[v] = 1
The vertex is visited, increase by .
c += 1
The edge will be a back edge and form a cycle if and vertex is already visited . If a cycle is detected, set . If no cycle is detected, continue the search from vertex .
for i in range(n):
if i != p and g[v][i]:
if used[i]: flag = 1
else: dfs(i, v)The main part of the program. Read the input value of .
n = int(input())
Count the number of visited vertices during the depth-first search in the variable . Set if there is no cycle in the graph. When a cycle is detected, becomes .
c = 0 flag = 0
All vertices are initially unvisited (initialize the list with zeroes).
used = [0] * n
Create an adjacency matrix , initially filled with zeroes.
g = [[0] * n for _ in range(n)]
Read the input adjacency matrix.
for i in range(n): g[i] = list(map(int, input().split()))
Start the depth-first search from vertex . Since it is the root of the tree, it has no parent. Pass the value as the second argument to the dfs function.
dfs(0, -1)
The graph is not a tree if there is a back edge or if the graph is not connected .
if flag or c != n:
print("NO")
else:
print("YES")Declare the adjacency matrix of the graph and the array .
#define MAX 101 int g[MAX][MAX], used[MAX];
The dfs function implements depth-first search from vertex .
void dfs(int v)
{Mark the vertex as visited.
used[v] = 1;
Vertex is visited, increase by .
c++;
Iterate over the vertices , that can be reached from . Moving from to is possible if:
There is an edge , that is ;
The vertex is not visited
If both conditions are true, we continue the depth-first search from vertex .
for (int i = 1; i <= n; i++)
if (g[v][i] && !used[i]) dfs(i);
}The main part of the program. Read the input value of .
scanf("%d", &n); Count the number of edges in the graph in the variable .
Edges = 0;
All vertices are initially unvisited (initialize the array with zeroes).
memset(used, 0, sizeof(used));
Read the adjacency matrix . Count the number of edges in the graph.
for (i = 1; i <= n; i++)
for (j = 1; j <= n; j++)
{
scanf("%d", &g[i][j]);
Edges += g[i][j];
}Since the graph is undirected, edges and are considered the same. Divide the value of by .
Edges /= 2;
Count the number of visited vertices during the depth-first search in variable .
c = 0;
Start the depth-first search from the vertex .
dfs(1);
The graph is a tree if the number of edges in it equals , and also if it is connected .
if ((Edges == n - 1) && (c == n)) printf("YES\n");
else printf("NO\n");Python implementation — checking the conditions 1) and 2)
The dfs function implements depth-first search from vertex .
def dfs(v): global c
Mark the vertex as visited.
used[v] = 1
The vertex is visited, increase by .
c += 1
Iterate over the vertices , that can be reached from . Moving from to is possible if:
There is an edge , that is ;
The vertex is not visited
If both conditions are true, we continue the depth-first search from vertex .
for i in range(1, n + 1):
if g[v][i] and not used[i]: dfs(i)The main part of the program. Read the input value of .
n = int(input())
Count the number of edges in the graph in the variable .
Edges = 0
All vertices are initially unvisited (initialize the array with zeroes).
used = [0] * (n + 1)
Create an adjacency matrix , initially filled with zeroes.
g = [[0] * (n + 1) for _ in range(n + 1)]
Read the adjacency matrix . Count the number of edges in the graph.
for i in range(1, n + 1): g[i] = [0] + list(map(int, input().split())) Edges += sum(g[i])
Since the graph is undirected, edges and are considered the same. Divide the value of by .
Edges //= 2
Count the number of visited vertices during the depth-first search in variable .
c = 0
Start the depth-first search from the vertex .
dfs(1)
The graph is a tree if the number of edges in it equals , and also if it is connected .
if Edges == n - 1 and c == n:
print("YES")
else:
print("NO")A connected undirected graph without loops or multiple edges is given. It is allowed to delete edges from the graph. The goal is to obtain a tree.
Input. The first line contains two integers – the number of vertices and the number of edges in the graph. The following pairs of integers each represent an edge. It is guaranteed that the graph is connected.
Output. Print pairs of integers — the edges that form a tree. The edges can be printed in any order.

4 4 1 2 2 3 3 4 4 1
1 2 2 3 3 4
Perform a depth-first search starting from the first vertex. Build the depth-first search tree and print all of its edges.
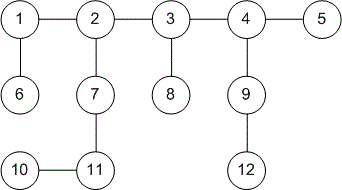
Example
The graph given in the example has the following structure:
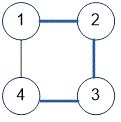
When the depth-first search is started from vertex , the traversal will go through the edges: .
The adjacency matrix of the graph is stored in the array .
#define MAX 101 int g[MAX][MAX], used[MAX];
The dfs function performs a depth-first search starting from vertex . Each edge that is part of the depth-first search tree is printed.
void dfs(int v)
{
used[v] = 1;
for (int i = 1; i <= n; i++)
if (g[v][i] && !used[i])
{
printf("%d %d\n",v,i);
dfs(i);
}
}The main part of the program. Read the input data.
scanf("%d %d",&n,&m);
memset(g,0,sizeof(g)); memset(used,0,sizeof(used));
while(m--)
{
scanf("%d %d",&a,&b);
g[a][b] = g[b][a] = 1;
}Start a depth-first search from the first vertex.
dfs(1);
You are given a tree, which is a simple connected graph without cycles.
Find the maximum number of edges that can be removed from the tree to obtain a forest where each connected component contains an even number of nodes.
For example, in the tree with nodes shown below, you can remove at most edge to create an even forest.

Input. The first line contains two integers is even) and — the number of nodes and edges. Each of the next lines contains two integers representing the nodes connected by an edge in the tree. The root of the tree is node .
Output. Print the maximum number of edges that can be removed.

10 9 2 1 3 1 4 3 5 2 6 1 7 2 8 6 9 8 10 8
2
The task is to decompose the tree into connected components with an even number of vertices, while maximizing the number of such components.
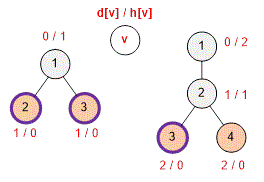
We'll perform a depth-first search starting from vertex , which is the root of the tree. For each vertex , we'll determine the number of vertices in the subtree rooted at . If this number is even, we'll remove the edge connecting to its parent in the depth-first search.
For the root (vertex ), the size of the entire tree is even. However, there is no edge connecting vertex to its parent, so we must subtract from the result obtained using the above algorithm.
Example
Consider the tree shown in the example. Next to each vertex is the size of the subtree when that vertex is considered as the root. Vertices , and have subtrees with an even number of vertices. Since vertex is the root and does not have an edge leading to a parent, we remove two edges: and .

The tree has been decomposed into connected components, each containing an even number of vertices.
Declare the arrays.
#define MAX 101 int g[MAX][MAX], used[MAX];
The dfs function performs a depth-first search starting from vertex and returns the number of vertices in the subtree rooted at .
int dfs(int v)
{
used[v] = 1;In the variable , compute the number of vertices in the subtree rooted at .
int s = 1;
Iterate over the children of vertex . Add the values of to .
for (int i = 1; i <= n; i++)
if (g[v][i] && !used[i]) s += dfs(i);If the size of the subtree is even, remove the edge between and its parent.
if (s % 2 == 0) res++;
Return the number of vertices in the subtree rooted at .
return s; }
The main part of the program. Read the input data and build the graph.
scanf("%d %d", &n, &m);
for (i = 0; i < m; i++)
{
scanf("%d %d", &a, &b);
g[a][b] = g[b][a] = 1;
}Start a depth-first search from vertex . In the variable , count the number of removed edges.
res = 0; dfs(1);
Since there is no edge from to its parent, print .
printf("%d\n", res - 1);Python implementation
The dfs function performs a depth-first search starting from vertex and returns the number of vertices in the subtree rooted at .
def dfs(v): used[v] = 1
In the variable , compute the number of vertices in the subtree rooted at .
s = 1
Iterate over the children of vertex . Add the values of to .
for i in range(1, n + 1):
if g[v][i] and not used[i]:
s += dfs(i)If the size of the subtree is even, remove the edge between and its parent.
if s % 2 == 0:
global res
res += 1Return the number of vertices in the subtree rooted at .
return s
The main part of the program. Read the input data and build the graph.
n, m = map(int, input().split()) g = [[0] * (n + 1) for _ in range(n + 1)] used = [0] * (n + 1) for _ in range(m): a, b = map(int, input().split()) g[a][b] = g[b][a] = 1
Start a depth-first search from vertex . In the variable , count the number of removed edges.
res = 0 dfs(1)
Since there is no edge from to its parent, print .
print(res - 1)
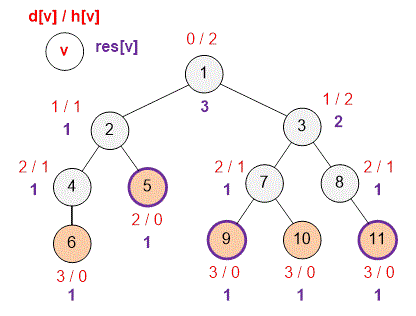
Given the structure of a company, your task is to calculate for each employee the number of their subordinates.
Input. The first line has an integer — the number of employees. The employees are numbered , , ..., , and employee is the general director of the company.
After this, there are integers: for each employee , , ... , their direct boss in the company.
Output. Print integers: for each employee , , ..., the number of their subordinates.

5 1 1 2 3
4 1 1 0 0
The structure of the company is a tree. For each vertex in the tree, determine the number of vertices in the subtree where is the root. The number of subordinates for employee will be (since employee is not his own subordinate).
Initiate a depth-first search starting from vertex , which corresponds to the general director of the company. If are the children of vertex , then
If vertex is a leaf in the tree, set .
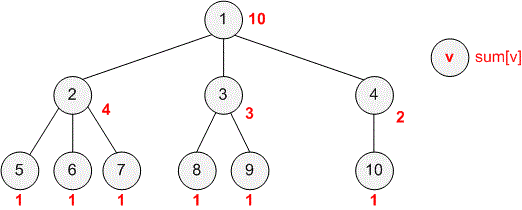
Example
Consider the example. Next to each employee (vertex of the graph), the number of their subordinates is indicated.
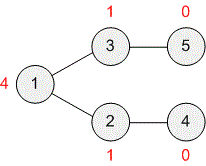
The tree is stored in the adjacency list .
vector<vector<int> > g;
The dfs function performs a depth-first search from vertex and returns the number of vertices in the subtree rooted at . Vertex is the parent of in the depth-first search.
int dfs(int v, int p)
{Initially, the subtree rooted at contains only the vertex .
sum[v] = 1;
Consider the edge . If , add to the number of vertices in the subtree rooted at .
for (int to : g[v])
if (to != p) sum[v] += dfs(to, v);Return the number of vertices in the subtree rooted at .
return sum[v]; }
The main part of the program. Read the input data. Construct a tree.
scanf("%d", &n);
g.resize(n + 1);
for (i = 2; i <= n; i++)
{
scanf("%d", &x);For employee , its immediate supervisor in the company is .
g[i].push_back(x); g[x].push_back(i); }
Start the depth-first search from vertex .
sum.resize(n + 1); dfs(1, -1);
Print the answer. The number of subordinates of employee is equal to .
for (i = 1; i <= n; i++)
printf("%d ", sum[i] - 1);
printf("\n");Java implementation
import java.util.*;
public class Main
{
static ArrayList<Integer>[] g;
static int sum[];
static int n;
static int dfs(int v, int p)
{
sum[v] = 1;
for(int to : g[v])
if (to != p) sum[v] += dfs(to,v);
return sum[v];
}
@SuppressWarnings("unchecked")
public static void main(String[] args)
{
Scanner con = new Scanner(System.in);
n = con.nextInt();
g = new ArrayList[n+1]; // unchecked
sum = new int[n+1];
for (int i = 0; i <= n; i++)
g[i] = new ArrayList<Integer>();
for (int i = 2; i <= n; i++)
{
int x = con.nextInt();
g[i].add(x);
g[x].add(i);
}
dfs(1,-1);
for (int i = 1; i <= n; i++)
System.out.print(sum[i] - 1 + " ");
System.out.println();
con.close();
}
} Python implementation
Increase the stack for recursion.
import sys sys.setrecursionlimit(1000000)
The dfs function performs a depth-first search from vertex and returns the number of vertices in the subtree rooted at . Vertex is the parent of in the depth-first search.
def dfs(v, p):
Initially, the subtree rooted at contains only the vertex .
sum[v] = 1
Consider the edge . If , add to the number of vertices in the subtree rooted at .
for to in g[v]:
if to != p: sum[v] += dfs(to,v)Return the number of vertices in the subtree rooted at .
return sum[v]
The main part of the program. Read the number of employees.
n = int(input())
Initialize the adjacency list of the graph .
g = [[] for _ in range(n+1)]
Read the input data. Construct a tree.
lst = list(map(int, input().split())) for i in range(2,n+1): a = lst[i-2]
For employee , its immediate supervisor in the company is .
g[a].append(i) g[i].append(a)
Initialize the list .
sum = [0] * (n + 1)
Start the depth-first search from vertex .
dfs(1,-1)
Print the answer. The number of subordinates of employee is equal to .
for i in range(1, n+1): print(sum[i] - 1,end=" ")
A tree consisting of vertices is given.
The diameter of a tree is the maximum distance between two vertices. Find the diameter of the given tree.
Input. The first line contains an integer — the number of vertices in the tree. The vertices are numbered from to .
Each of the following lines describes an edge and contains two integers and , indicating that there is an edge between vertices and .
Output. Print one integer — the diameter of the tree.

5 1 2 1 3 3 4 3 5
3
Perform a depth-first search starting from any vertex, for example, from vertex . Find the vertex farthest from and denote it as vertex . Then, start a depth-first search from vertex to find the vertex that is farthest from , which we'll denote as vertex . The distance between vertices and will then be the maximum possible and equal to the diameter of the tree.
Example
Consider the tree from the example.
The diameter of the tree is . The maximum distance is achieved, for example, between vertices and .
Exercise
Find the diameter of the tree.
Store the input tree in the adjacency list . Store the shortest distances from the source to each vertex in the array .
vector<vector<int>> g; vector<int> dist;
The dfs function performs a depth-first search from vertex . The shortest distance from the source to vertex is . The parent of vertex in the depth-first search is .
void dfs(int v, int d, int p = -1)
{Store the shortest distance from the source to vertex in .
dist[v] = d;
Iterate over all edges . For each son to of vertex (where is not a parent of ) initiate a depth-first search. The distance from the source to vertex will be .
for (int to : g[v])
if (to != p) dfs(to, d + 1, v);
}The main part of the program. Read the input data.
scanf("%d", &n);
g.resize(n + 1);
dist.resize(n + 1);Construct an undirected tree.
for (i = 1; i < n; i++)
{
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}Find the shortest distances from vertex to all other vertices. The vertex farthest from it is .
dfs(1, 0, -1);
a = max_element(dist.begin(), dist.begin() + n + 1) –
dist.begin();Find the shortest distances from vertex to all other vertices. The vertex farthest from it is .
dfs(a, 0, -1);
b = max_element(dist.begin(), dist.begin() + n + 1) –
dist.begin();Print the diameter of the tree — the shortest distance from to .
printf("%d\n", dist[b]);A tree consisting of vertices is given.
For each vertex, determine the maximum distance to any other vertex.
Input. The first line contains an integer — the number of vertices in the tree. The vertices are numbered from to .
The next lines describe the edges: each line contains two integers and , indicating that there is an edge between vertices and .
Output. Print integers. For each vertex from to , print the maximum distance to any other vertex in the tree.

5 1 2 1 3 3 4 3 5
2 3 2 3 3
Using two depth-first search (DFS) runs, we find the diameter of the tree.
Since a tree is a connected graph without cycles, both depth-first search (DFS) and breadth-first search (BFS) correctly find the shortest distances from the starting vertex to all others.
Let and be two vertices that are the farthest apart — that is, they define the diameter of the tree.
Compute the shortest distances from vertex to all other vertices and store them in the array , and from vertex — in the array .
Then, for each vertex , the greatest distance to any other vertex is equal to:
Example
Consider a tree from the example.
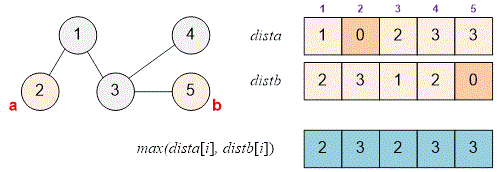
The diameter of the tree can be, for example, the path between vertices and .
The input tree is stored as an adjacency list .
The shortest distances from vertices and are stored in the arrays and , respectively.
vector<vector<int>> g; vector<int> dista, distb;
The function dfs performs a depth-first search starting from vertex .
The parameter represents the shortest distance from the source to vertex .
The results are stored in the array .
The parameter indicates the parent of vertex during the traversal.
void dfs(int v, int d, vector<int>& dist, int p = -1)
{Store the shortest distance from the source to vertex in .
dist[v] = d;
Iterate over all edges . For each child of vertex (i.e., a vertex to that is not the parent of ), perform a depth-first search.
for (int to : g[v])
if (to != p) dfs(to, d + 1, dist, v);
}The main part of the program. Read the input data.
scanf("%d", &n);
g.resize(n + 1);
dista.resize(n + 1);
distb.resize(n + 1);Construct an undirected tree.
for (i = 1; i < n; i++)
{
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}Compute the shortest distances from vertex . The vertex farthest from it is vertex .
dfs(1, 0, dista, -1); a = max_element(dista.begin() + 1, dista.begin() + n + 1) - dista.begin();
Next, compute the shortest distances from vertex and store them in the array . The vertex farthest from turns out to be vertex . The distance between vertices and is the diameter of the tree.
dfs(a, 0, dista, -1); b = max_element(dista.begin() + 1, dista.begin() + n + 1) - dista.begin();
Then compute the shortest distances from vertex and store them in the array .
dfs(b, 0, distb, -1);
For each vertex , print the distance to the farthest vertex from it.
for (i = 1; i <= n; i++)
printf("%d ", max(dista[i], distb[i]));
printf("\n");Python implementation
Increase the recursion stack size.
import sys sys.setrecursionlimit(1000000)
The function dfs performs a depth-first search starting from vertex .
The parameter represents the shortest distance from the source to vertex .
The results are stored in the array .
The parameter indicates the parent of vertex during the traversal.
def dfs(v, d, dist, p =- 1):
Store the shortest distance from the source to vertex in .
dist[v] = d
Iterate over all edges . For each child of vertex (i.e., a vertex to that is not the parent of ), perform a depth-first search.
for to in g[v]:
if to != p:
dfs(to, d + 1, dist, v)The main part of the program. Read the input data.
n = int(input()) g = [[] for _ in range(n + 1)] dista = [0] * (n + 1) distb = [0] * (n + 1)
Construct an undirected tree.
for _ in range(n - 1): u, v = map(int, input().split()) g[u].append(v) g[v].append(u)
Compute the shortest distances from vertex . The vertex farthest from it is vertex .
dfs(1, 0, dista) a = dista.index(max(dista[1:]))
Next, compute the shortest distances from vertex and store them in the array . The vertex farthest from turns out to be vertex . The distance between vertices and is the diameter of the tree.
dfs(a, 0, dista) b = dista.index(max(dista[1:]))
Then compute the shortest distances from vertex and store them in the array .
dfs(b, 0, distb)
For each vertex , print the distance to the farthest vertex from it.
result = [max(dista[i], distb[i]) for i in range(1, n + 1)] print(*result)
Roman's parents gave him an undirected, connected, weighted graph with vertices and edges. Roman wants to find the total length of all paths between every pair of vertices in the graph. The length of a path is defined as the sum of the weights of the edges it includes. Since the path from vertex to vertex is the same as the path from to , Roman treats them as a single path and does not distinguish between them.
Input. The first line contains an integer — the number of vertices in the graph.
Each of the next lines describes an edge and contains three integers: the numbers of the two vertices connected by the edge (vertices are numbered from to ), and the weight of the edge.
Output. Print the total length of all distinct paths between all pairs of vertices, modulo .

3 1 2 1 1 3 3
8
6 1 2 5 1 3 1 2 4 2 2 5 4 2 6 3
90
Perform a depth-first search starting from an arbitrary vertex of the tree. Consider an edge with weight . Let the number of vertices in the subtree rooted at be . Then, there are vertices on one side of the edge and vertices on the other side. The edge is included in distinct paths between pairs of vertices. Therefore, its contribution to the total length of all paths is . We just need to iterate over all edges using depth-first search and sum up their contributions to the overall path length.
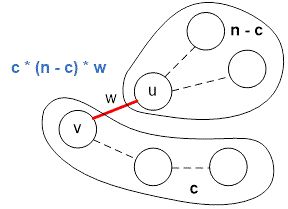
Example
The graphs given in the examples have the following structure:
Consider the contribution of the edges to the total length of all paths in the first example.
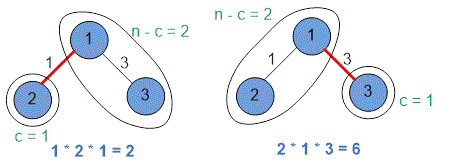
The edge with weight belongs to two paths:
;
;
Its contribution to the total sum is .
The edge with weight belongs to two paths:
;
;
Its contribution to the total sum is .
The total length of all paths is .
In the second example, let us consider the contribution of the edge with weight to the total length of all paths.
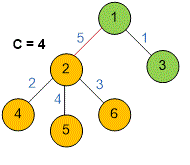
The number of vertices in the subtree rooted at vertex is (including vertex itself). Then, on the other side of the edge there are vertices. Therefore, the number of distinct paths passing through the edge is .
Indeed, these are all pairs of vertices where one lies in the subtree of vertex , and the other lies outside of it:
The contribution of the edge with weight to the total length of all paths is
Declare the value of the modulo as .
#define MOD 1000000000
The input weighted graph is stored in an adjacency list .
vector<vector<pair<int,int> > > g;
The function dfs performs a depth-first search starting from vertex and returns the number of vertices in the subtree rooted at (including itself). The number of such vertices is counted in the variable . Initially, set since the subtree already includes vertex .
int dfs(int v, int p = -1)
{
int cnt = 1;
for (auto edge : g[v])
{
int to = edge.first;
int w = edge.second;Consider the edge with weight . Let be the number of vertices in the subtree rooted at vertex . Then, one side of the edge contains vertices, and the other side contains vertices. The edge is included in different paths between pairs of vertices. Thus, the contribution of the edge to the total length of all paths is
if (to != p)
{
int c = dfs(to, v);
res = (res + 1LL * c * (n - c) * w) % MOD;
cnt += c;
}
}
return cnt;
}The main part of the program. Read the input weighted graph into the adjacency list .
scanf("%d", &n);
g.resize(n + 1);
for (i = 1; i < n; i++)
{
scanf("%d %d %d", &u, &v, &d);
g[u].push_back({v, d});
g[v].push_back({u, d});
}Start a depth-first search from vertex . The vertices of the graph are numbered from to .
dfs(1);
Print the answer.
printf("%lld\n",res);Java implementation
import java.util.*;
import java.io.*;
class Edge
{
int to;
int weight;
public Edge(int to, int weight)
{
this.to = to;
this.weight = weight;
}
}
public class Main
{
static int MOD = 1000000000;
static ArrayList<Edge>[] g;
static int n, m;
static long res;
static int dfs(int v, int p)
{
int cnt = 1;
for(Edge edge : g[v])
{
int to = edge.to;
int w = edge.weight;
if (to != p)
{
int c = dfs(to, v);
res = (res + 1L * c * (n - c) * w) % MOD;
cnt += c;
}
}
return cnt;
}
public static void main(String[] args)
{
FastScanner con = new FastScanner(System.in);
n = con.nextInt();
g = new ArrayList[n+1]; // unchecked
for (int i = 0; i <= n; i++)
g[i] = new ArrayList<Edge>();
for (int i = 1; i < n; i++)
{
int u = con.nextInt();
int v = con.nextInt();
int d = con.nextInt();
g[u].add(new Edge(v,d));
g[v].add(new Edge(u,d));
}
dfs(1,-1);
System.out.println(res);
}
}
class FastScanner
{
BufferedReader br;
StringTokenizer st;
public FastScanner(InputStream inputStream)
{
br = new BufferedReader(new InputStreamReader(inputStream));
st = new StringTokenizer("");
}
public String next()
{
while (!st.hasMoreTokens())
{
try
{
st = new StringTokenizer(br.readLine());
} catch (Exception e)
{
return null;
}
}
return st.nextToken();
}
public int nextInt()
{
return Integer.parseInt(next());
}
}Python implementation
Declare the value of the modulo as .
MOD = 1000000000
The function dfs performs a depth-first search starting from vertex and returns the number of vertices in the subtree rooted at (including itself). The number of such vertices is counted in the variable . Initially, set since the subtree already includes vertex .
def dfs(v, p = -1): global res cnt = 1 for to, w in g[v]:
Consider the edge with weight . Let be the number of vertices in the subtree rooted at vertex . Then, one side of the edge contains vertices, and the other side contains vertices. The edge is included in different paths between pairs of vertices. Thus, the contribution of the edge to the total length of all paths is
if to != p:
c = dfs(to, v)
res = (res + c * (n - c) * w) % MOD
cnt += c
return cntThe main part of the program. Read the input data.
n = int(input()) g = [[] for _ in range(n + 1)] res = 0 for _ in range(n - 1): u, v, d = map(int, input().split()) g[u].append((v, d)) g[v].append((u, d))
Start a depth-first search from vertex . The vertices of the graph are numbered from to .
dfs(1)
Print the answer.
print(res)
A rooted tree consisting of vertices is given. Each vertex is painted in one of colors. For each vertex , determine the number of distinct colors that appear in the subtree rooted at .
Input. The first line contains a single integer . The following lines describe the vertices of the tree. The -th line contains two integers and , where is the parent of vertex , and is the color of vertex . For the root of the tree, .
Output. Print integers — one for each vertex from to . For each vertex, print the number of distinct colors in the subtree rooted at that vertex.
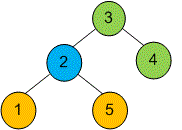
5 2 1 3 2 0 3 3 3 2 1
1 2 3 1 1
Perform a depth-first traversal of the tree starting from the root. For each vertex , maintain a set , which accumulates the colors of all vertices in the subtree rooted at .
If is a child of vertex during the traversal, then the set should be merged into .
The number of distinct colors in the subtree rooted at vertex is equal to the size (cardinality) of the set .
Example
The color of each vertex is shown on the left. The set of colors in its subtree is shown on the right.
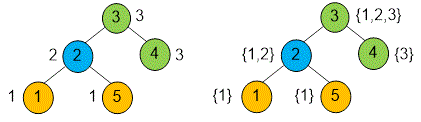
The array stores the color of vertex . The set will accumulate the colors that appear in the subtree rooted at vertex .
The directed tree is represented as an adjacency list . The array stores the number of distinct colors in the subtree rooted at vertex .
#define MAX 1000010 int color[MAX], res[MAX]; set<int> s[MAX]; vector<vector<int> > g;
The function dfs performs a depth-first traversal of the tree starting from vertex .
void dfs(int v)
{First, the color of vertex itself is added to the set .
s[v].insert(color[v]);
Iterate over the tree edges .
for (int to : g[v])
{
dfs(to);For each edge , merge the set into . If the size of is smaller than the size of , swap them first. Then, the content of the smaller set is added to the larger set .
if (s[v].size() < s[to].size()) s[v].swap(s[to]);
s[v].insert(s[to].begin(), s[to].end());Clear the set — it is no longer needed.
s[to].clear(); }
After that, store the number of distinct colors in the subtree in , which is the size of the set .
res[v] = s[v].size(); }
The main part of the program. Read the input data.
scanf("%d",&n);
g.resize(n+1);
for(i = 1; i <= n; i++)
{
scanf("%d %d",&p,&c);
g[p].push_back(i);
color[i] = c;
}Start the depth-first search from the root of the tree — the vertex with index .
dfs(0);
Print the answer.
for(i = 1; i <= n; i++)
printf("%d ",res[i]);
printf("\n");After a long and busy work week, the residents of Manchester and Liverpool decided to go hiking for the weekend. While walking through the forest, they came across a unique tree consisting of vertices. The vertices of the tree are numbered from to , and each one is painted in one of possible colors.
To fight off boredom, they decided to test their logical thinking. The root of the tree is vertex . For each vertex, the participants decided to find its nearest ancestor that shares the same color.
Input. The first line contains two integers and — the number of vertices in the tree and the number of possible colors.
The second line contains integers: the -th of them indicates the parent of vertex .
The third line contains integers — the colors of the vertices. Each color is an integer from to , inclusive.
Output. Print integers in a single line: for each vertex, print the number of its nearest ancestor with the same color. If no such ancestor exists, print .
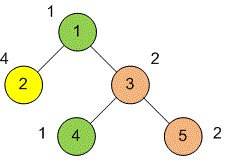
5 4 1 1 3 3 1 4 2 1 2
-1 -1 -1 1 3
Let us consider a simplified version of the problem. Suppose all the vertices of the tree are painted the same color. We initialize an empty stack and perform a depth-first search starting from the root of the tree. When entering a vertex , push it onto the stack. When the processing of vertex is complete, remove the top element from the stack (which will be vertex itself). After the DFS is finished, the stack will once again be empty.
Question: What will be on the top of the stack at the moment we enter vertex , just before we push onto the stack?
Now let us move on to solving the original problem. We create stacks — one for each color (for example, using a vector of stacks). Initially, all stacks are empty. Perform a DFS starting from the root of the tree — vertex . The processing of a vertex , painted in color , includes the following steps:
If the stack is not empty, its top element contains the number of the vertex that is the nearest ancestor of vertex with the same color. If the stack is empty, such a vertex does not exist, and the answer for vertex should be .
Push vertex onto the stack .
Recursively perform a depth-first search from all children of vertex .
After finishing the processing of vertex , remove it from the stack .
During the depth-first search, when we are at vertex , the stacks contain information about the colors of all vertices along the unique path from the root to vertex . In particular, the stack stores the numbers of all vertices on this path that are colored with . These vertices are pushed onto the stack in the order they are visited during the DFS.
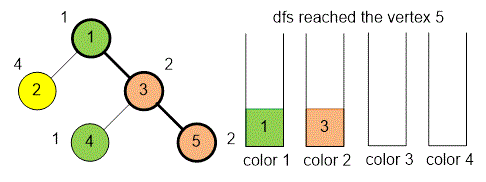
Example
When the depth-first search reaches vertex , two out of the stacks will be empty (those corresponding to colors and ).
Stack number (for color ) will contain vertex , and stack number (for color ) will contain vertex . Since vertex has color , its nearest ancestor with the same color is at the top of stack number .
Therefore, the nearest ancestor of vertex with the same color is vertex .
Declare the arrays.
vector<int> col, res; vector<vector<int> > g; vector<stack<int> > s;
The dfs function performs a depth-first search starting from vertex .
void dfs(int v)
{Vertex has color .
int color = col[v];
The number of the nearest ancestor of vertex with the same color is stored in .
if(s[color].empty())
res[v] = -1;
else
res[v] = s[color].top();Push vertex onto the stack corresponding to its color.
s[color].push(v);
Iterate over all children of vertex and recursively perform a depth-first search from each of them.
for (int to : g[v])
dfs(to);After processing vertex is complete (i.e., upon exiting it), remove it from the stack corresponding to its color.
s[color].pop(); }
The main part of the program. Read the input data. Construct a tree.
scanf("%d %d", &n, &c);
g.resize(n + 1);
for(i = 2; i <= n; i++)
{
scanf("%d",&val);
g[val].push_back(i);
}Read the colors of the tree's vertices.
col.resize(n + 1);
for(i = 1; i <= n; i++)
scanf("%d",&col[i]);Start a depth first search from vertex .
s.resize(c + 1); res.resize(n + 1); dfs(1);
Print the answer.
for(i = 1; i <= n; i++)
printf("%d ",res[i]);
printf("\n");Python implementation
Increase the recursion stack size.
import sys sys.setrecursionlimit(1000000)
The dfs function performs a depth-first search starting from vertex .
def dfs(v):
Vertex has color .
color = col[v]
The number of the nearest ancestor of vertex with the same color is stored in .
if not s[color]:
res[v] = -1
else:
res[v] = s[color][-1]Push vertex onto the stack corresponding to its color.
s[color].append(v)
Iterate over all children of vertex and recursively perform a depth-first search from each of them.
for to in g[v]:
dfs(to)After processing vertex is complete (i.e., upon exiting it), remove it from the stack corresponding to its color.
s[color].pop()
The main part of the program. Read the input data. Construct a tree.
n, c = map(int, input().split()) lst = list(map(int, input().split())) g = [[] for _ in range(n + 1)] for i in range(2, n + 1): val = lst[i - 2] g[val].append(i)
Read the colors of the tree's vertices.
col = [0] * (n + 1) col[1:] = list(map(int, input().split()))
Start a depth first search from vertex .
s = [[] for _ in range(c + 1)] res = [0] * (n + 1) dfs(1)
Print the answer.
print(*res[1:])
In his spare time, Farmer John created his own video-sharing platform called MooTube. On MooTube, his cows can record, publish, and discover lots of funny videos. So far, the cows have uploaded videos, numbered from to .
However, Farmer John doesn't fully understand how to help his cows find new videos they might enjoy. He wants to implement a recommendation system for each video — a list of "recommended videos" based on their similarity to videos already watched.
To determine how similar two videos are, John introduces a relevance metric. He manually evaluates pairs of videos and assigns each pair a relevance score. Using these pairs, John builds a network where each video is a node in a graph, and the selected pairs are connected by edges with the given relevance values.
For convenience, John selects the pairs in such a way that there is exactly one path between any two videos — in other words, the video network forms a tree.
He decides that the relevance between two videos should be defined as the minimum relevance among all edges along the path connecting them.
Now, Farmer John wants to choose a value such that, for any video on MooTube, all other videos with relevance at least to it will be displayed as recommendations. However, he worries that too many recommendations might distract his cows from producing milk, so he wants to precisely estimate how many videos would be recommended for various values of .
Farmer John turns to you for help: you are given several queries, each consisting of a value and a video number. For each query, you need to determine how many other videos would be recommended if the minimum required relevance is .
Input. The first line contains two integers and — the number of videos and the number of queries, respectively.
The next lines describe pairs of videos whose relevance has been manually evaluated by Farmer John. Each of these lines contains three integers и , , meaning that videos and are connected by an edge with relevance .
Then follow lines, each describing one of Farmer John’s queries. The -th line contains two integers and — meaning that in the -th query, Farmer John wants to know how many videos will be recommended for video if the minimum acceptable relevance for recommendations is .
Output. Print lines. In the -th line, output the answer to Farmer John's -th query.

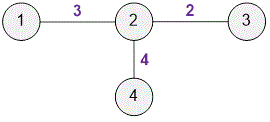
Example. Farmer John has established the following connections between videos:
Video and video have a relevance of ,
Video and video have a relevance of ,
Video and video have a relevance of .
Based on this data, we can compute the relevance between other pairs of videos:
Video and video : relevance = ,
Video and video : relevance = ,
Video and video : relevance = .
Now let’s see which videos will be recommended for the following queries:
From video with , videos , and will be recommended.
From video with , videos and will be recommended.
From video with , no videos will be recommended.
4 3 1 2 3 2 3 2 2 4 4 1 2 4 1 3 1
3 0 2
For each query given by the pair , perform a depth-first or breadth-first search starting from vertex . During the traversal, only follow edges whose relevance is at least .
Count the number of reachable vertices , excluding the starting vertex . The value of is the answer to the query .
Example
Farmer John has established the following connections between videos:
Video and video have a relevance of ,
Video and video have a relevance of ,
Video and video have a relevance of .
Based on this data, we can compute the relevance between other pairs of videos:
Video and video : relevance = ,
Video and video : relevance = ,
Video and video : relevance = .
Now let’s see which videos will be recommended for the following queries:
From video with , videos , and will be recommended.
From video with , videos and will be recommended.
From video with , no videos will be recommended.
Store the input graph in an adjacency list .
vector<vector<pair<int, int>>> g;
The bfs function performs a breadth-first search starting from the vertex and returns the number of visited vertices, excluding the vertex itself. During the search, we only move along edges whose weight is at least the given value .
int bfs(int start, int k)
{The shortest distance array is not needed in this problem — it's sufficient to simply track whether a vertex is visited. If vertex is visited, set .
vector<int> used(n + 1); used[start] = 1;
Initialize a queue and add the starting vertex to it.
queue<int> q; q.push(start);
The number of visited vertices during the breadth-first search (excluding the starting vertex ) is counted in the variable .
int res = 0;
Start the breadth-first search.
while (!q.empty())
{Extract the vertex from the queue .
int v = q.front(); q.pop();
Iterate over all edges adjacent to vertex .
for (auto edge : g[v])
{Consider the edge with weight .
int to = edge.first;
int kto = edge.second;If the edge weight is less than , skip this edge (moving along it is forbidden).
if (kto < k) continue;
If the vertex is not visited yet, add it to the queue, mark it as visited, and increment the counter by .
if (used[to] == 0)
{
q.push(to);
used[to] = 1;
res++;
}
}
}Return the answer to the query.
return res; }
The main part of the program. Read the input data.
scanf("%d %d", &n, &qu);
g.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d %d", &p, &q, &r);Add an undirected edge with weight to the adjacency list.
g[p].push_back({ q, r });
g[q].push_back({ p, r });
}Process the queries one by one.
while (qu--)
{
scanf("%d %d", &k, &v);Perform a breadth-first search (BFS) starting from vertex and print the number of vertices visited during the BFS.
printf("%d\n", bfs(v, k));
}Algorithm implementation — depth first search
Store the input graph in an adjacency list .
vector<vector<pair<int, int>>> g;
The dfs function performs a depth-first search starting from vertex and returns the number of visited vertices. During the search, we only traverse edges whose weight is not less than the given value .
int dfs(int v, int k)
{Mark vertex as visited.
used[v] = 1;
Count the number of vertices visited in the subtree rooted at during the depth-first search in the variable .
int res = 1;
Iterate over all edges adjacent to vertex .
for (auto edge : g[v])
{Consider the edge with weight .
int to = edge.first;
int kto = edge.second;If the weight is less than , skip this edge (moving along it is forbidden).
if (kto < k) continue;
If vertex is not visited yet, perform a depth-first search starting from it. The number of vertices visited in the subtree rooted at is added to .
if (used[to] == 0)
res += dfs(to, k);
}
return res;
}The main part of the program. Read the input data.
scanf("%d %d", &n, &qu);
g.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d %d", &p, &q, &r);Add an undirected edge with weight to the adjacency list.
g[p].push_back({ q, r });
g[q].push_back({ p, r });
}Process the queries one by one.
while (qu--)
{
scanf("%d %d", &k, &v);Perform a depth-first search starting from vertex . Print the number of vertices visited during the depth-first search, excluding the starting vertex .
used.assign(n + 1, 0);
printf("%d\n", dfs(v, k) - 1);
}The tree with vertices is given. The edges of the tree have weights of only or . Let’s find the XOR sum between all pairs of vertices. Compute the sum of all XOR sums.
Input. The first line contains the number of vertices in the graph. The next lines describe the edges. Each line contains three integers: the numbers of the vertices connected by the edge (vertices are numbered from to ) and the weight of the edge ( or ).
Output. Print the sum of XOR sums between all pairs of vertices.
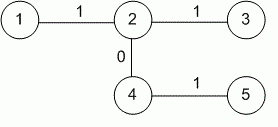
5 1 2 1 2 3 1 2 4 0 4 5 1
6
Using depth-first search, compute the XOR sum between vertex and all other vertices. Store the XOR sum between vertex and in . Let be the number of ones and be the number of zeros in the array . Then the answer to the problem will be .
Example
Consider the graph provided in the example.
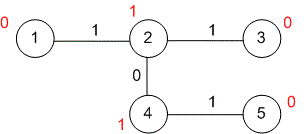
Next to each vertex , the XOR sum between and is written. If for some vertices and , then the XOR sum between them is equal to , thus contributing to the total sum. The XOR sum for each pair of vertices , for which , contributes to the total sum.
Therefore, the answer is equal to the number of pairs of vertices for which . This number is equal to . The pairs of vertices that contribute to the total sum are: .
Store the input graph in the adjacency list . Declare an array .
vector<vector<pair<int,int> > > g; vector<int> x;
The dfs function implements a depth-first search that computes the XOR sum between vertices and . The current XOR sum between and is represented by . The parent of vertex is .
void dfs(int v, int cur_xor, int p = -1)
{
x[v] = cur_xor;
for (auto z : g[v])
{
int to = z.first;
int w = z.second;
if (to != p) dfs(to, cur_xor ^ w, v);
}
}The main part of the program. Read the input graph.
scanf("%d", &n);
g.resize(n + 1);
x.resize(n + 1);
for (i = 1; i < n; i++)
{
scanf("%d %d %d", &u, &v, &d);
g[u].push_back({v, d});
g[v].push_back({u, d});
}Start the depth-first search from vertex .
dfs(1, 0, -1);
Compute the number of and in the array .
ones = 0; for (i = 1; i <= n; i++) if (x[i] == 1) ones++; zeroes = n - ones;
Print the answer.
printf("%lld\n", 1LL * ones * zeroes);Python implementation
The dfs function implements a depth-first search that computes the XOR sum between vertices and . The current XOR sum between and is represented by . The parent of vertex is .
def dfs(v, cur_xor = 0, p = -1):
x[v] = cur_xor
for to, w in g[v]:
if to != p:
dfs(to, cur_xor ^ w, v)The main part of the program. Read the input graph.
n = int(input()) g = [[] for _ in range(n + 1)] for _ in range(n - 1): u, v, d = map(int, input().split()) g[u].append((v, d)) g[v].append((u, d))
Initialize the list .
x = [0] * (n + 1)
Start the depth-first search from vertex .
dfs(1)
Compute the number of and in the array .
ones = sum(x) zeroes = n - ones
Print the answer.
print(ones * zeroes)
A tree with vertices numbered from to is given. The -th edge of the tree connects vertices and . Vertex is colored with color (in this problem, colors are represented by integers).
A vertex is considered good if the shortest path from vertex to vertex does not contain any other vertex with the same color as vertex , except for itself.
Find all good vertices.
Input. The first line contains an integer — the number of vertices.
The second line contains integers — the colors of the vertices: .
Each of the following lines contains two integers and — the edges of the tree.
Output. Print all good vertices, one per line, in ascending order of their indices.

6 2 7 1 8 2 8 1 2 3 6 3 2 4 3 2 5
1 2 3 4 6
10 3 1 4 1 5 9 2 6 5 3 1 2 2 3 3 4 4 5 5 6 6 7 7 8 8 9 9 10
1 2 3 5 6 7 8
Start a depth-first search from vertex . When entering vertex with color , increment the value of by . The value represents how many times the color has appeared on the path from vertex to vertex (inclusive). If this color appears exactly once on the path, then vertex is considered good, and we add it to the result set.
When exiting vertex , decrement the value of by .
Example
The graph from the first example looks as follows:
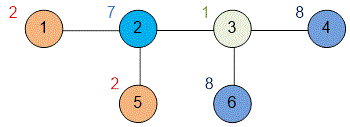
Vertex is not good because on the path , vertices and have the same color.
Vertex is good because on the path , the colors of all intermediate vertices differ from the color of vertex .
Store the input graph in the adjacency list . Declare the arrays.
vector<int> used, color; vector<vector<int>> g; set<int> st;
The dfs function implements depth-first search. The variable is the parent of vertex .
void dfs(int v, int par)
{Vertex has the color . Mark that a vertex with this color is visited on the path from vertex .
used[color[v]]++;
The value indicates how many times the color has appeared on the path from vertex to vertex (inclusive). If this color appears exactly once on the path, then vertex is considered good, and we add it to the result set .
if (used[color[v]] == 1) st.insert(v);
Iterate over all edges originating from vertex . If vertex is not the parent of , start a depth-first search from . In this case, the parent of becomes .
for (int to : g[v])
if (to != par) dfs(to, v);When exiting vertex , decrement the value of by .
used[color[v]]--; }
The main part of the program. Read the number of vertices and the array of colors.
scanf("%d", &n);
color.resize(n + 1);
for (i = 1; i <= n; i++)
scanf("%d", &color[i]);Read the graph.
used.resize(100001);
g.resize(n + 1);
for (i = 1; i < n; i++)
{
scanf("%d %d", &x, &y);
g[x].push_back(y);
g[y].push_back(x);
}Start a depth-first search from vertex .
dfs(1, 1);
Print the good vertices. They are contained in the set .
for (int val : st)
printf("%d\n", val);You are given a tree with vertices and edges. The vertices are numbered from to , and the -th edge connects vertices and .
You have colors available. For each vertex in the tree, you choose one of the colors to paint it, subject to the following condition:
If the distance between two different vertices and is less than or equal to two, then and have different colors.
How many ways are there to color the tree? Find the answer modulo .
Input. The first line contains two numbers and . Each of the following lines contains two integers and .
Output. Print the number of ways to color the tree modulo
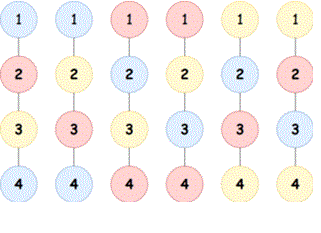
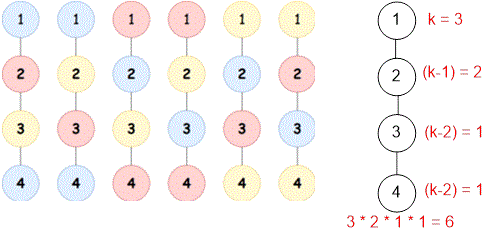
4 3 1 2 2 3 3 4
6
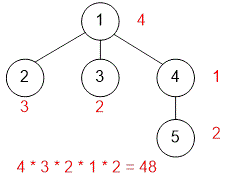
5 4 1 2 1 3 1 4 4 5
48
Let's start coloring the tree from vertex . It can be colored with colors.
Suppose we are at vertex . If it has no parent (), then its children can be colored with colors. If has a parent, then its children can be colored with colors. Since the distance between the children of vertex is , they cannot be colored with the same color.
If vertex has a parent, then the first child of can be colored with colors, the second child with colors, and so on.
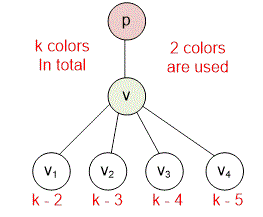
It remains to multiply the numbers of colors that can be used to color each vertex.
Example
For the first example, there are ways of coloring:
Let's consider the second test. Next to each vertex, we'll indicate the number of colors it can be colored with. For example, vertex can be colored with colors, as its color must not match the colors of vertices and . The total number of ways to color the tree is equal to .
Store the input graph in the adjacency list . Declare a constant for the modulo.
#define MOD 1000000007 vector<vector<int>> g;
The dfs function returns the number of ways to color the tree rooted at vertex modulo . The parent of vertex is . Vertex can be colored with colors.
int dfs(int v, int col, int p = -1)
{
long long res = col;We are at vertex . In the variable , we keep track of the number of colors that cannot be used to paint the children of vertex . Initially, set , since the children of vertex cannot have the same color as vertex . If vertex has a parent (), then the children of vertex also cannot have the color of 's parent.
int cnt = 1; if (p >= 0) cnt++;
Iterate over the sons of the vertex .
for (int to : g[v])
if (to != p)
{The vertex can be colored with colors. With each son, the value will be increased by .
res = (res * dfs(to, k - cnt, v)) % MOD;
cnt++;
}
return res;
}The main part of the program. Read the input data.
scanf("%d %d", &n, &k);
g.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}Start the depth-first search from vertex . Vertex number can be colored with colors.
res = dfs(1, k);
Print the answer.
printf("%lld\n", res);Python implementation
Set the maximum depth of the Python interpreter stack to the specified limit.
import sys sys.setrecursionlimit(1000000)
Declare a constant for the modulo.
MOD = 1000000007
The dfs function returns the number of ways to color the tree rooted at vertex modulo . The parent of vertex is . Vertex can be colored with colors.
def dfs(v, col, p = -1): res = col
We are at vertex . In the variable , we keep track of the number of colors that cannot be used to paint the children of vertex . Initially, set , since the children of vertex cannot have the same color as vertex . If vertex has a parent (), then the children of vertex also cannot have the color of 's parent.
cnt = 1 if p >= 0: cnt += 1
Iterate over the sons of the vertex .
for to in g[v]:
if to != p:The vertex can be colored with colors. With each son, the value will be increased by .
res = (res * dfs(to, k - cnt, v)) % MOD
cnt += 1
return resThe main part of the program. Read the input data.
n, k = map(int, input().split()) g = [[] for _ in range(n + 1)] for _ in range(n - 1): a, b = map(int, input().split()) g[a].append(b) g[b].append(a)
Start the depth-first search from vertex . Vertex number can be colored with colors.
res = dfs(1, k)
Print the answer.
print(res)
There are cities in the country and bidirectional roads, such that it is possible to travel from any city to any other city using only these roads. The cities are numbered with integers from to inclusive.
Initially, all roads are considered to be in bad condition, but the government plans to improve the state of some of them. The citizens will be satisfied with the improvements if there is no more than one bad road on the path from the capital, located in city , to any other city.
Determine the number of ways to improve the quality of some roads to meet this requirement. Since the answer can be very large, output it modulo .
Input. The first line contains a single integer — the number of cities in the country. The second line contains positive integers , describing the roads in the country. The number indicates that there is a road connecting city and city .
Output. Print the number of ways to improve the quality of the roads modulo .
3 1 1
4
6 1 2 2 1 5
15
Let denote the number of ways to improve the quality of roads for the subtree rooted at vertex . Let represent a child of vertex .
If the road remains in bad condition, then all roads in the subtree rooted at vertex must be improved.
If the road is improved, then the number of ways to improve the roads for the subtree rooted at vertex is equal to .
Let be the children of . Then
If is a leaf (a vertex with no children), then let .
Example
Consider the examples provided in the problem statement. For each vertex , we'll record the value of .
In the first example, there are ways to improve the quality of roads such that on the path from city 1 to any other city, there is no more than one bad road. Bad roads are represented by dashed lines, while improved roads are represented by solid lines.

All calculations are performed modulo .
#define MOD 1000000007
The dfs function computes the value of — the number of ways to improve the quality of roads for the subtree rooted at vertex . The parent of is vertex .
long long dfs(int v, int p = -1)
{
long long s = 1;If are the children of , then
for (int to : g[v])
if (to != p)
{
long long sub = dfs(to, v);
s = (s * (sub + 1)) % MOD;
}
return s;
}Read the input data. Construct a tree.
scanf("%d", &n);
g.resize(n + 1);
for (i = 2; i <= n; i++)
{
scanf("%d", &p);
g[i].push_back(p);
g[p].push_back(i);
}Compute and print the result.
res = dfs(1);
printf("%lld\n", res);On clear summer days, Nyusha enjoys catching butterflies in the fresh air. But today, she encountered a particularly cunning butterfly — it flew into a labyrinth and tried to hide from her inside.
The labyrinth consists of rooms, numbered from to , some of which are connected by corridors. It is known that there is exactly one simple path between any two rooms, passing only through the corridors. In other words, the labyrinth forms a tree with vertices and edges.
The entrance to the labyrinth is located in room number . A leaf is defined as any room connected to exactly one other room and not being the root (i.e., not room ). Each leaf contains an exit from the labyrinth. The butterfly starts its flight from room , heading toward one of the exits. It moves at a constant speed, never turns around, and travels through one corridor per minute, moving to a neighboring room. All corridors are of equal length.
To catch the butterfly, Nyusha decided to enlist the help of some friends. Initially, each of them can take position in any room that contains an exit. As soon as the butterfly begins its journey from the entrance toward some exit, the friends may immediately start moving from their rooms toward the entrance. They move at the same speed as the butterfly. If any of them encounters the butterfly — whether in a room or in the middle of a corridor — it is considered caught. However, if the butterfly reaches an exit without encountering any of the friends, it successfully escapes to freedom.
Help Nyusha determine the minimum number of friends needed to guarantee catching the butterfly, regardless of which exit it chooses.
Input. The first line contains a single integer — the number of rooms in the labyrinth.
The following lines describe the corridors connecting the rooms. Each line contains two integers and — the indices of the rooms connected by a corridor.
It is guaranteed that the given corridor system forms a tree.
Output. Print a single integer — the minimum number of friends required to guarantee that the butterfly will be caught.
3 1 2 1 3
2
4 1 2 2 3 2 4
1
Perform a depth-first search starting from vertex . For each vertex, compute two values:
— the distance from vertex to vertex . If is the parent of , then
— the distance from vertex v to the nearest leaf in the subtree rooted at . If are the children of vertex , then
If is a leaf of the tree, set .
Next, perform a second depth-first search. During this traversal, compute the value — the minimum number of friends that need to be placed in some of the leaves of the subtree rooted at vertex in order to guarantee catching the butterfly, assuming it chooses to fly into this subtree.
If , then . In this case, it is enough to place one friend in the leaf with the minimal depth in the subtree rooted at vertex : they will reach vertex no later than the butterfly flying from the root.
Otherwise, if are the children of vertex , then
If the butterfly is not caught at vertex itself, we must be prepared to intercept it in any of the subtrees of 's children.
The final answer to the problem is the value .
Example
In the first example (shown in the left diagram), two friends are required, and they should be placed at the two exits. The butterfly can fly from vertex either to vertex or to vertex . In either case, it will be intercepted by one of Nyusha's friends.
In the second example (shown in the right diagram), one friend is enough, who can be placed at either of the two exits — vertex or . The butterfly will fly from vertex to vertex in one minute. During that same time, the friend will reach vertex and catch the butterfly there.
Let us consider the next example.
Nyusha will need three friends to catch the butterfly.
Declare a constant for infinity and arrays.
#define INF 2000000000 vector<vector<int> > g; vector<int> d, h, res;
The function dfs performs a depth-first search starting from vertex and returns the value . Here, is the parent of vertex , and cnt is the distance from vertex to . During the traversal, the values and are computed for each vertex .
int dfs(int v, int p = -1, int cnt = 0)
{The value , which equals the distance from vertex to , is stored in .
d[v] = cnt; int height = INF;
Iterate over all the children of the vertex . Consider the edge . If equals the parent of , skip it and move to the next child.
for (int to : g[v])
if (to != p) In the variable compute the value
where are the children of vertex .
If , then vertex is a leaf, and set . Otherwise rerturn
return h[v] = (height == INF) ? 0 : 1 + height; }
The function dfs2 performs a depth-first search starting from vertex and returns the value . Here, is the parent of vertex .
int dfs2(int v, int p = -1)
{
int s = 0;Let be the children of vertex . In the variable , compute the sum:
for (int to : g[v])
if (to != p)
{
dfs2(to, v);
s += res[to];
}If , then one friend is sufficient, and . Otherwise
return res[v] = (h[v] <= d[v]) ? 1 : s; }
The main part of the program. Read the input data. Construct a graph.
scanf("%d", &n);
g.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}Initialize the arrays.
d.resize(n + 1); h.resize(n + 1); res.resize(n + 1);
Run two depth-first searches. The first traversal computes the values of and for each vertex .
dfs(1); dfs2(1);
Print the answer — the minimum number of friends needed to catch the butterfly.
printf("%lld\n", res[1]);Kefa decided to celebrate his first big salary by going to a restaurant.
He lives near an unusual park. The park is a rooted tree with vertices, rooted at vertex . Kefa's house is located at vertex as well. Unfortunately for our hero, the park is inhabited by cats, and Kefa has already identified the vertices where the cats are located.
The leaf vertices of the park contain restaurants. Kefa wants to choose a restaurant, but he is very afraid of cats. Therefore, he will not go to a restaurant if, on the path from his house to the restaurant, he encounters more than consecutive vertices with cats.
Your task is to help Kefa count the number of restaurants he can safely visit.
Input. The first line contains two integers and — the number of vertices in the tree and the maximum number of consecutive vertices with cats that Kefa can tolerate.
The second line contains integers , where each is either (there is no cat at vertex ) or (there is a cat at vertex ).
The following lines contains the tree's edges in the format , where and are vertices connected by an edge.
It is guaranteed that this set of edges forms a tree.
Output. Print the number of leaf vertices that Kefa can reach if there are no more than consecutive vertices with cats on the way from his house.
7 1 1 1 0 0 0 0 1 1 2 1 3 2 4 2 5 3 6 3 7
2
8 2 1 1 0 1 0 1 0 1 1 2 2 3 2 5 2 6 3 4 6 7 6 8
2
Start a depth first search from vertex , where Kefa's house is located. One of the parameters of the dfs function will store the number of consecutive vertices with cats. If at vertex this number exceeds , we'll not continue the depth-first search from this vertex. We count the number of visited leaf vertices. A vertex is a leaf if its degree is and it is not a root (vertex ).
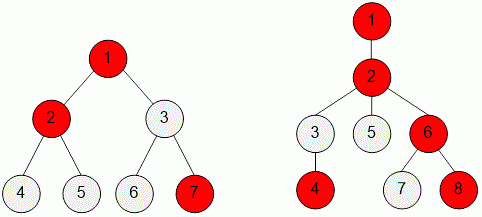
Example
Let’s consider the trees from the first and second examples.

In the first example, Kefa can pass through only one consecutive vertex with a cat. He will be able to reach the restaurants located at vertices and .
In the second example, Kefa can pass through two consecutive vertices with cats. He will be able to reach the restaurants located at vertices and .
The location of the cats is stored in the array . The tree is stored in the adjacency list .
vector<int> cats; vector<vector<int> > g;
The dfs function performs a depth-first search from vertex and returns the number of restaurants that can be reached from this vertex (under the condition that no more than consecutive vertices with cats are encountered on the path to them). The parent of vertex is the vertex . The number of consecutive vertices with cats encountered up to and including vertex is .
int dfs(int v, int prev, int cnt)
{If more than consecutive cats are already encountered, further depth-first search from vertex is not continued.
if (cnt > m) return 0;
If we are at a leaf, increase the number of accessible restaurants.
if (g[v].size() == 1 && prev != -1) return 1;
In the variable count the number of restaurants reachable from vertex .
int res = 0;
Iterate over all edges originating from vertex . If the vertex is a parent of , do not move to this vertex.
for (int to : g[v])
if (to != prev)
{If there is no cat at the vertex , set . Otherwise, assign . The variable stores the number of consecutive vertices with cats up to and including vertex .
int c = (cats[to] == 0) ? 0 : cnt + 1;
Start a depth-first search from vertex .
res += dfs(to, v, c);
}Return the result.
return res; }
The main part of the program. Read the input data.
scanf("%d %d", &n, &m);
cats.resize(n + 1);
for (i = 1; i <= n; i++)
scanf("%d", &cats[i]);Construct a tree.
g.resize(n + 1);
for (i = 1; i < n; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}Print the result. The dfs function, called from vertex , returns the answer to the problem. Since vertex has no parent, we pass the value as the second parameter. Starting from vertex , we have encountered cats.
printf("%d\n", dfs(1, -1, cats[1]));Python implementation
The dfs function performs a depth-first search from vertex and returns the number of restaurants that can be reached from this vertex (under the condition that no more than consecutive vertices with cats are encountered on the path to them). The parent of vertex is the vertex . The number of consecutive vertices with cats encountered up to and including vertex is .
def dfs(v, prev, cnt):
If more than consecutive cats are already encountered, further depth-first search from vertex is not continued.
if cnt > m:
return 0If we are at a leaf, increase the number of accessible restaurants.
if len(g[v]) == 1 and prev != -1:
return 1In the variable count the number of restaurants reachable from vertex .
res = 0
Iterate over all edges originating from vertex . If the vertex is a parent of , do not move to this vertex.
for to in g[v]:
if to != prev:If there is no cat at the vertex , set . Otherwise, assign . The variable stores the number of consecutive vertices with cats up to and including vertex .
c = 0 if cats[to] == 0 else cnt + 1
Start a depth-first search from vertex .
res += dfs(to, v, c)
Return the result.
return res
The main part of the program. Read the input data.
n, m = map(int, input().split()) cats = [0] + list(map(int, input().split()))
Construct a tree.
g = [[] for _ in range(n + 1)] for _ in range(n - 1): a, b = map(int, input().split()) g[a].append(b) g[b].append(a)
Print the result. The dfs function, called from vertex , returns the answer to the problem. Since vertex has no parent, we pass the value as the second parameter. Starting from vertex , we have encountered cats.
print(dfs(1, -1, cats[1]))
A tree with vertices is given. Vertex is considered the root. There is exactly one simple path between any two vertices.
Let denote the number of edges on the path from vertex to vertex .
Find the number of vertex pairs such that the following equality holds:
Input. The first line contains a single integer — the number of vertices in the tree.
Each of the next lines contains two integers, describing the edges of the tree: the pairs of vertices connected by an edge.
Output. Print a single integer — the number of pairs for which holds.
5 1 2 2 3 2 4 4 5
13
The condition holds for every pair of vertices where is an ancestor of in the depth-first search starting from vertex .
Let us consider an example:

;
;
Let us define the depth of a vertex as the number of vertices on the path from the root (vertex ) to . In the diagram, the depth is written next to each vertex.
Now, fix a vertex and ask the question: how many vertices are there such that the condition is satisfied?
For example, for , there are such vertices: . Note that . Thus, for a fixed vertex , there are exactly suitable vertices .
To solve the problem, we need to compute the depth for each vertex in the tree, and then find the sum of all these depths across the tree.
Example
Let us consider the graph from the example. Next to each vertex, we write its depth.
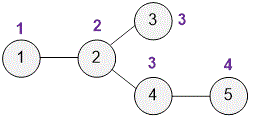
The sum of the depths of all vertices is .
Define the graph's adjacency list as . The depths of the vertices are stored in the array .
vector<vector<int> > g; vector<int> h;
The dfs function computes the depth of each vertex . The parent of vertex is the vertex .
int dfs(int v, int p)
{
for (int to : g[v])Consider the edge . If the vertex is not the parent of vertex , compute its depth and perform a depth first search starting from it.
if (to != p)
{
h[to] = h[v] + 1;
dfs(to, v);
}
return h[v];
}The main part of the program. Read the number of vertices in the tree.
scanf("%d", &n);
g.resize(n + 1);Construct a tree.
for (i = 2; i <= n; i++)
{
scanf("%d %d", &a, &b);
g[a].push_back(b);
g[b].push_back(a);
}Set the depth of vertex to be .
h.resize(n + 1); h[1] = 1;
Start a depth first search from the vertex .
dfs(1, -1);
Compute the answer — the sum of the depths of all vertices.
res = 0; for (i = 1; i <= n; i++) res += h[i];
Print the answer.
printf("%lld\n", res);You are given a binary tree, which is an acyclic connected undirected graph containing vertices and edges. Each vertex has a degree of no more than . The root is the vertex number , with its degree not exceeding .
Unfortunately, the root of the tree is infected. The following process is repeated times:
Huseyn either selects a vertex that is not yet infected (and not yet removed) and removes it along with all its incident edges, or he takes no action.
After that, the infection spreads to every vertex connected by an edge to an already infected vertex (all previously infected vertices remain infected).
Help Huseyn determine the maximum number of vertices he can save from infection (note that removed vertices are not considered saved).
Input. The first line contains the number of vertices in the tree .
Each of the following lines contains two integers and , representing an edge of the tree.
It is guaranteed that the graph is a binary tree with the root at vertex .
Output. Print a single integer — the number of saved vertices.
4 1 2 2 3 2 4
2
7 1 2 1 5 2 3 2 4 5 6 5 7
2
For each vertex , compute the number of vertices in the subtree where it is the root. If are the children of vertex , then
If vertex is a leaf of the tree, then .
Let be the number of saved vertices in the subtree with root , assuming that currently vertex (and only it in the subtree) is infected.
If vertex has only one child , then (the removed vertex is not considered saved).
Let vertex have two children and (each vertex has a degree of at most ). Then we have two options:
Remove and recursively save the vertices in the subtree with root . The number of saved vertices will be sum .
Remove and recursively save the vertices in the subtree with root . The number of saved vertices will be .
Among the two options, choose the one that maximizes the number of saved vertices.
Consider the depth-first search process when examining the edge .

Let be the second child of vertex . We need to compute the value . Let's try to find it using only the vertices and . We know that:
From which it follows that:
Thus,
Iterate over the children of the vertex and compute:
Example
In the first example, Huseyn is able to save two vertices, and , by choosing vertex number as his first move.|
Consider the second example. Next to each vertex , place the labels . The vertices chosen by Huseyn are displayed in green.
For example,
Declare the arrays.
#define MAX 300005 int sum[MAX], dp[MAX]; vector<vector<int>> g;
The function dfs performs a depth-first search starting from vertex . The parent of vertex is .
void dfs(int v, int p = -1)
{Initialize the variables and .
sum[v] = 1; dp[v] = 0;
Perform a depth-first search starting from the children of vertex .
for (int to : g[v])
if (to != p)
{
dfs(to, v);
sum[v] += sum[to];
}Compute the value of .
for (int to : g[v])
if (to != p)
{
dp[v] = max(dp[v], sum[to] - 1); // if 1 son
dp[v] = max(dp[v], dp[to] + sum[v] - sum[to] - 2);
}
}The main part of the program. Read the input data.
scanf("%d", &n);
g.clear(); g.resize(n + 1);
memset(dp, 0, sizeof(dp));
memset(sum, 0, sizeof(sum));
for (i = 1; i < n; i++)
{
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
}Perform a depth-first search starting from vertex .
dfs(1);
Print the answer.
printf("%d\n", dp[1]);