Rekursiyanı araşdırmaq

Bu dərsin məqsədi tələbələrə rekursiya anlayışını tanıtmaq, onun əsaslarını anlamaq və proqramlaşdırmada tətbiqini mənimsəməkdir. Bu dərsin sonunda tələbələr aşağıdakıları bacarmalıdırlar:

• Rekursiyanı və onun əsas xüsusiyyətlərini təyin etmək.

• Rekursiv funksiyaların iş mexanizmini anlamaq.

• Sadə rekursiv alqoritmləri tətbiq etmək.

• Rekursiya üçün uyğun ssenariləri müəyyənləşdirmək.

Giriş:

• Proqramlaşdırmada problem həll etmə texnikaları haqqında qısa bir müzakirə ilə başlayın.

• Real həyat nümunəsi ilə rekursiya anlayışını tanıdın.

• Rekursiyanı bir problemin həlli üçün funksiyanın özünü birbaşa və ya dolayısı ilə çağırdığı proqramlaşdırma texnikası kimi təyin edin.

• Rekursiyanın əsas xüsusiyyətlərini vurğulayın: baza halı, rekursiv hal və özünə istinad.

Rekursiv Funksiyaların Anlaşılması:

• Sadə bir nümunə (faktorial, qüvvət $x^n$ və ya Fibonacci ardıcıllığı) istifadə edərək rekursiv funksiyaların mexanizmini izah edin.

• Rekursiv funksiyaların addım-addım necə işlədiyini göstərərək baza halının əhəmiyyətini vurğulayın.

• Çağırış yığımı (call stack) və onun rekursiv funksiya çağırışlarında necə istifadə edildiyini müzakirə edin.

• Sonsuz rekursiya anlayışını və ondan necə qaçınmağı izah edin.

Rekursiv Alqoritmlərin Tətbiqi:

• Rekursiya üçün uyğun proqramlaşdırma problemləri təqdim edin.

• Tələbələri bu problemləri rekursiya ilə həll etmək üçün cütlərə və ya kiçik qruplara bölün.

• Tələbələri baza halı və rekursiv halı təyin etməyə diqqət edərək sıfırdan rekursiv funksiyalar yazmağa təşviq edin.

• Lazım olduqda tələbələrə bələdçilik etmək və kömək etmək üçün qruplar arasında dolaşın.

Yekunlaşdırma və Təcrübə:

• Hər qrupun rekursiv həllərini sinifə təqdim etmələrini təmin edin.

• Müxtəlif rekursiv yanaşmaların səmərəliliyini və oxunaqlılığını müzakirə edin.

• Məşq zamanı rast gəlinən ümumi çətinliklər və ya yanlış təsəvvürləri həll edin.

• Tələbələrin fərdi və ya qrup şəklində işləmələri üçün əlavə təcrübə problemləri təqdim edin.

Nəticə:

• Dərsdə öyrənilən əsas məqamları ümumiləşdirin, proqramlaşdırmada rekursiyanın gücü və çox yönlülüyünü vurğulayın.

• Tələbələri rekursiyanı öz layihələrində və tapşırıqlarında araşdırmağa təşviq edin.

Ev Tapşırığı:

• Dərsdə öyrənilən anlayışları gücləndirmək üçün spesifik problemlər üçün rekursiv alqoritmlərin tətbiqi və ya kod kitabxanalarında mövcud rekursiv funksiyaların təhlili kimi ev tapşırığı tapşırıqları verin.

Qiymətləndirmə:

• Tələbələrin sinif müzakirələrində iştirakı, rekursiv proqramlaşdırma problemlərini həll etmək bacarığı və rekursiv həlləri izah etməkdəki aydınlığı vasitəsilə başa düşmələrini qiymətləndirin.

• Rekursiya anlayışlarının və tətbiq bacarıqlarının fərdi olaraq mənimsənilməsini ölçmək üçün ev tapşırıqlarını nəzərdən keçirin.

Giriş

Proqramlaşdırmada problem həll etmə texnikaları haqqında qısa bir müzakirə ilə başlayın

Proqramlaşdırmada, problem həll etmə hər dəfə kod yazdığınız zaman istifadə edəcəyiniz əsas bacarıqdır. Rekursiyanın xüsusiyyətlərinə keçməzdən əvvəl, problem həll etmə texnikaları haqqında qısa bir müzakirə aparaq.

Problem həll etməyi bir səyahət kimi düşünün. Problemlə (programınızın həll etməli olduğu bir tapşırıq) başlayırsınız və A nöqtəsindən (problem) B nöqtəsinə (həll) necə çatmağı anlamağa çalışırsınız. Bu səyahət problemi daha kiçik, idarə olunan hissələrə bölməyi, daxil olan və çıxan məlumatları təyin etməyi və arzu olunan nəticəyə çatmaq üçün bir plan qurmağı əhatə edir.

Proqramçılar problemləri effektiv şəkildə həll etmək üçün bir neçə texnikadan istifadə edirlər. Budur, əsas olanlardan bəziləri:

• Problemi Anlamaq: Problemi həll etmədən əvvəl onu tam anlamalısınız. Bu, problem ifadəsini oxumaq və təhlil etmək, daxil olan və çıxan məlumatları təyin etmək və hər hansı bir qeyri-müəyyənliyi aydınlaşdırmaq deməkdir.

• Böl və Fəth et: Bir çox mürəkkəb problem daha kiçik, idarə olunan alt problemlərə bölünərək həll edilə bilər. Böl və fəth et yanaşması hər bir alt problemi ayrı-ayrılıqda həll etməyə və sonra həlləri birləşdirərək daha böyük problemi həll etməyə imkan verir.

• Alqoritmik Düşüncə: Alqoritmlər problemləri həll etmək üçün addım-addım prosedurlardır. Problemlə üzləşdiyiniz zaman həlli məntiqi addımlar ardıcıllığına bölərək alqoritmik düşünməyə çalışın.

• Abstraksiya: Abstraksiya problemin əsas detallarına diqqət yetirmək, lakin əlaqəsiz və ya yayındırıcı məlumatları gözardı etmək deməkdir. Lazımsız detalları soyutlamaqla problemi sadələşdirə və vacib olanlara diqqət yetirə bilərsiniz.

• Təkrar və Rekursiya: Təkrar bir dövr və ya təlimatlar ardıcıllığının təkrarlanması ilə problemi həll etməyi əhatə edir. Digər tərəfdən, rekursiya problemi eyni problemin daha kiçik hallarına bölərək həll etməyi əhatə edir. Həm təkrar, həm də rekursiya proqramlaşdırmada tez-tez rast gəlinən güclü problem həll etmə texnikalarıdır.

Bu problem həll etmə texnikalarına yiyələnməklə, rekursiyanı əhatə edənlər də daxil olmaqla, geniş spektrli proqramlaşdırma problemlərini həll etməyə daha yaxşı hazırlaşacaqsınız. Beləliklə, rekursiyanı daha dərindən araşdırdığımız zaman, bu problem həll etmə strategiyalarını yadda saxlayın — onlar sizin proqramlaşdırma alət dəstinizdə dəyərli alətlər olacaqdır.

Real həyat nümunəsi ilə rekursiya anlayışını tanıdın

Yaxşı, gəlin bir anlıq kodlaşdırmadan uzaqlaşaq və rekursiyanı real həyat nümunələri ilə düşünək. Tutaq ki, qarşınızda Rus matrioşka kuklaları var. Bu kuklalar müxtəlif ölçülərdə olur, hər biri bir-birinin içərisinə yerləşir.

İndi gəlin, dəstdəki hər kuklanı açma prosesini təsvir edə biləcəyimizi düşünək. Siz ən böyük kukla ilə başlayırsınız və onu açdıqda, içərisində daha kiçik bir kukla tapırsınız. Sonra həmin daha kiçik kuklanı açırsınız, içərisində daha da kiçik birini tapırsınız və belə davam edirsiniz, ta ki, ən kiçik kuklaya çatana qədər - içərisində heç bir şey olmayan kukla.

Bu, rekursiv bir proses kimi qəbul edilə bilər. Niyə? Çünki hər bir kukla quruluş baxımından digərlərinə bənzəyir və hər bir kuklanı açma hərəkəti eyni şəkildədir – içəridə daha kiçik bir kuklanın olub olmadığını yoxlamaq.

Proqramlaşdırma baxımından, rekursiya da eyni şəkildə işləyir. Rus matrioşka kuklalarını açmaq əvəzinə, biz funksiyaları və ya metodları "açırıq". Rekursiv funksiya, bir problemi həll etmək üçün ya birbaşa, ya da dolayısı ilə özü-özünü çağıran funksiyadır.

Beləliklə, matrioşka kuklaları ilə olduğu kimi, rekursiya da bir problemi daha kiçik, oxşar alt problemlərə bölərək həll etməyi əhatə edir, ta ki problem o qədər kiçik və sadə olana qədər ki, onu birbaşa həll edə bilirik. Bu ən kiçik, sadə problemin versiyasına baza halı deyirik.

Rekursiyanı Rus matrioşka kuklaları kimi real həyat nümunələri ilə anlamaqla, onun proqramlaşdırmaya necə tətbiq edildiyini və mürəkkəb problemləri aydın və zərif şəkildə həll etmək üçün necə güclü bir vasitə ola biləcəyini görə bilərik. Beləliklə, rekursiyanı daha dərindən araşdırdığımız zaman, bu vizual analoqu yadda saxlayın — anlayışı daha intuitiv şəkildə anlamağınıza kömək edəcəkdir.

Rekursiyanı bir problemin həlli üçün funksiyanın özünü birbaşa və ya dolayısı ilə çağırdığı proqramlaşdırma texnikası kimi təyin edin

İndi rekursiya anlayışını daha sadə terminlərlə izah edək. Təsəvvür edin ki, sizdə müəyyən bir vəzifəni yerinə yetirən funksiyanız var. İndi, bu funksiyanın özünü çağıra biləcəyini desəm nə düşünərdiniz? Bəli, doğru eşitdiniz! Buna rekursiya deyilir.

Rekursiya dövr kimi işləyir, amma şərt ödənənə qədər təlimatlar toplusunu təkrarlamaq əvəzinə, rekursiv funksiya müəyyən bir şərtə, adətən baza halına çatana qədər özünü təkrarlayır.

Gəlin bunu bir nümunə ilə izah edim. Tutaq ki, sizdə $n$ sayından $1$-ə qədər olan rəqəmləri çap edən "countDown" adlı funksiya var. Döngüdən istifadə etmək əvəzinə, "countDown"u rekursiv şəkildə müəyyən edə bilərik. Bu necə işləyir:

• "countDown" funksiyası $n$ adlı bir rəqəmi giriş olaraq qəbul edir.

• Əgər rəqəm $1$-dirsə (baza halı), sadəcə $1$-i çap edir və dayanır.

• Əgər rəqəm $1$-dən böyükdürsə, cari rəqəmi çap edir və sonra özünü daha kiçik rəqəmlə çağırır.

• Bu proses baza halına çatana qədər davam edir, bu zaman o, özünü çağırmağı dayandırır və rekursiya "geri açılır" (unwinds).

def countDown(n):
  # Base case: if n is 1, print it and stop recursion
  if n == 1:
    print(n)
  else:
    # Print current number
    print(n)
    # Call countDown function with the next smaller number
    countDown(n - 1)

# Example usage:
countDown(5)  # Prints numbers from 5 down to 1

Yəni, mahiyyət etibarilə, rekursiya problemi eyni problemin daha kiçik, oxşar alt problemlərinə bölərək həll etməyin bir yoludur və sonra bu alt problemləri yenidən və yenidən eyni funksiyanı çağıraraq həll edir, ta ki problemi birbaşa həll edə biləcəyimiz baza halına çatana qədər.

Rekursiya anlayışı bir az qarışıq ola bilər, amma onun prinsiplərini anlamaqla və təcrübə etməklə, onu proqramlaşdırma alət dəstinizdə güclü bir vasitə kimi istifadə edə biləcəksiniz.

Rekursiyanın əsas xüsusiyyətlərini vurğulayın: baza halı, rekursiv hal və özünə istinad

İndi rekursiyanın nə olduğunu və necə işlədiyini anladığımıza görə, onun əsas xüsusiyyətlərini dərinliklə araşdıraq. Rekursiya yaxşı işləyən bir maşın kimidir — onu düzgün işlətmək üçün xüsusi hissələri var. İndi vurğulayacağımız rekursiyanın üç əsas xüsusiyyəti var: baza halı, rekursiv hal və özünə istinad.

Baza Hali:

• Baza halını rekursiv funksiyamızın dayanma nöqtəsi kimi düşünün. Bu, funksiyaya özünü çağırmağı dayandırmağı və dəyərləri qaytarmağa başlamağı bildirən şərtdir.

• Baza halı olmadan, rekursiv funksiyamız özünü sonsuz şəkildə çağırmağa davam edərdi ki, bu da istəmədiyimiz sonsuz rekursiyaya səbəb olardı!

• Əvvəlki "countDown" funksiyası nümunəmizdə, baza halı $n$ $1$-ə çatanda idi. Bu zaman sadəcə $1$ çap etdik və funksiyanı çağırmağı dayandırdıq.

Rekursiv Hali:

• Rekursiv hal rekursiyanın sehrinin baş verdiyi yerdir. Bu, funksiyamızın özünü çağırdığı hissəsidir.

• Funksiyamız hər dəfə rekursiv halı ilə qarşılaşdıqda, baza halına bir addım daha yaxınlaşırıq. Problemi daha kiçik və daha kiçik alt problemlərə bölürük, ta ki baza halına çatana qədər.

• "countDown" funksiyasında, rekursiv hal $n$ $1$-dən böyük olduqda idi. Cari $n$ dəyərini çap etdik, sonra "countDown" funksiyasını yenidən $n–1$ ilə çağırdıq.

Özünə İstinad:

• Bu xüsusiyyət çox möhtəşəm səslənsə də, əslində çox sadədir. Özünə istinad funksiyamızın özünə istinad etməsi deməkdir.

• Rekursiv funksiyanı müəyyən edərkən, əslində deyirik ki, "Ey, funksiya, lazım olduqda özünü çağıra bilərsən."

• Bu özünə istinad edən təbiət rekursiyanın kompleks problemləri daha kiçik alt problemlərə bölərək həll etməsinə imkan verir.

• "countDown" funksiyasında, özünə istinadı funksiyanın özünü çağırdığı zaman gördük.

Beləliklə, yekun olaraq, rekursiyanın üç əsas xüsusiyyəti var:

1. baza halı, hansı ki, bizə nə zaman dayandırmağı bildirir;

2. rekursiv hal, hansı ki, problemi daha kiçik alt problemlərə bölür;

3. özünə istinad, hansı ki, funksiyanın özünü çağırmasına imkan verir.

Bu xüsusiyyətləri anlamaq və mənimsəmək rekursiyada ustalaşmaq və onu proqramlaşdırma səyahətinizdə effektiv şəkildə istifadə etmək üçün vacibdir.

Rekursiv Funksiyaların Anlaşılması

Sadə bir nümunə istifadə edərək rekursiv funksiyaların mexanizmini izah edin

Gəlin rekursiv funksiyaların mexanizmini sadə bir nümunə istifadə edərək izah edək. Nümunəmiz olaraq bir rəqəmin faktorialını hesablamağı götürək.

Müsbət tam ədədin $n$ faktorialı, $n!$ olaraq qeyd edilir və $n$-dən kiçik və ya bərabər olan bütün müsbət tam ədədlərin hasilidir. Məsələn, $5!$ (beş faktorial kimi oxunur) $5\cdot 4\cdot 3\cdot 2\cdot 1$-ə bərabərdir və bu da $120$-ə bərabərdir.

İndi bunu rekursiv bir funksiya ilə tətbiq edək:

# The function fact computes the factorial of the number n
def fact(n):
  if n == 0: return 1
  return n * fact(n-1)

# The main part of the program. Read the input value of n
n = int(input())

# Compute and print the answer
print(fact(n))

İndi bu rekursiv funksiyanın necə işlədiyini başa düşək:

Baza Hali:

• Faktorial funksiyamızda baza halı $n$ $0$-a bərabər olduqda. Bu hallarda, $0$-ın faktorialının həmişə $1$ olduğunu bilirik. Buna görə $1$ qaytarırıq.

Rekursiv Hali:

• $n$-in hər hansı digər dəyəri üçün ($n$ $1$-dən böyük olduqda), faktorialı rekursiv şəkildə hesablayırıq. Funksiyanı $n-1$ arqumenti ilə çağırırıq və nəticəni $n$-ə vururuq.

• Bu o deməkdir ki, $fact(n)$-i hesablamaq üçün əvvəlcə $fact(n-1)$-i hesablamalı və sonra nəticəni $n$-ə vurmalıyıq. Bu proses baza halına çatana qədər davam edir.

Bir nümunə ilə gəzək:

• $fact(5)$-i hesablamaq istəyiriksə, funksiya $fact(4)$, $fact(3)$, və s. çağıracaq, ta ki baza halına çatana qədər.

• Baza halına ($fact(1)$) çatanda, rekursiv çağırışlar "geri açılmağa" başlayır.

• Hər rekursiv çağırış nəticəsini qaytarır və onu cari $n$ dəyərinə vurur.

• Nəhayət, $fact(5)$-in nəticəsi $fact(4)\cdot 5$ kimi hesablanır, bu da $fact(3)\cdot 4\cdot 5$ kimi daha da hesablanır və s., ta ki son nəticə əldə olunana qədər.

Bu şəkildə rekursiya işləyir! Bu soğan təbəqələrini bir-bir açmağa bənzəyir - bir təbəqə açılır, sonra növbəti təbəqə, ta ki mərkəzə çatana qədər. Bu rekursiv prosesi anlamaq proqramlaşdırmada rekursiv funksiyalarda ustalaşmaq üçün vacibdir.

Rekursiv funksiyaların necə işlədiyini addım-addım göstərin, baza halının əhəmiyyətini vurğulayın

İndi rekursiv funksiyaların necə işlədiyini addım-addım izah edək və baza halının əhəmiyyətini vurğulayaq. Misal olaraq Fibonacci ardıcıllığından istifadə edək. Fibonacci ardıcıllığı, hər bir nömrənin özündən əvvəlki iki nömrənin cəmi olduğu bir sıra nömrələrdir, adətən $0$ və $1$ ilə başlayır. Beləliklə, ardıcıllıq belə gedir: $0,1,1,2,3,5,8,13$ və s.

Fibonacci ardıcıllığının forması belədir:

int tipinə uyğun olan ən böyük Fibonacci nömrəsi budur:

$n\le 40$ üçün int məlumat tipindən istifadə etmək kifayətdir.

Funksiya $fib(n)$ Fibonacci ardıcıllığının $n$-ci nömrəsini hesablasın. O zaman belə bir təkrar əlaqə əlaqəsi var:

İndi Fibonacci nömrələrini hesablamaq üçün rekursiv bir funksiya tətbiq edək:

# The function fib computes the n-th Fibonacci number
def fib(n):
  if (n == 0): return 0
  if (n == 1): return 1
  return fib(n - 1) + fib(n - 2)

# The main part of the program. Read the input value of n
n = int(input())

# Compute and print the answer
print(fib(n))

İndi bu rekursiv funksiyanın necə işlədiyini addım-addım izah edək:

Baza Hali:

• Baza hallar $n$ $0$ və $1$ olduqda. Bu hallarda Fibonacci nömrəsini birbaşa bilirik: $F_0=0$ və $F_1=1$. Bunlar əlavə hesablama tələb etməyən ən sadə hallardır.

Rekursiv Hali:

• $n$-in hər hansı digər dəyəri üçün ($n>1$ olduqda), Fibonacci nömrəsini rekursiv şəkildə hesablayırıq. Bunu edərkən ardıcıllığın əvvəlki iki mövqeyindəki Fibonacci nömrələrini ($fib(n-1)$ və $fib(n-2)$) toplayırıq.

• Bu o deməkdir ki, $fib(n)$-i hesablamaq üçün əvvəlcə $fib(n-1)$ və $fib(n-2)$-i hesablamaq və sonra onların nətic ələrini toplamaq lazımdır. Bu proses baza halına çatana qədər davam edir.

Bir nümunə ilə gəzək:

• $fib(4)$-ü hesablamaq istəyiriksə, funksiya $fib(3)$ və $fib(2)$ çağıracaq.

• $fib(3)$ daha sonra $fib(2)$ və $fib(1)$, $fib(2)$ isə $fib(1)$ və $fib(0)$ çağıracaq.

• $fib(1)$ və $fib(0)$ baza hallarıdır, beləliklə onlar $1$ və $0$ qaytarır.

• $fib(1)$ və $fib(0)$-ın nəticələri olduqdan sonra, $fib(2)$ onları toplayacaq $(0+1=1)$.

• $fib(3)$ də oxşar şəkildə $fib(2)$ və $fib(1)$-in nəticələrini toplayacaq $(1+1=2)$.

• Nəhayət, $fib(4)$ $fib(3)$ və $fib(2)$-ni toplayacaq $(2+1=3)$ və nəticəni əldə edəcəyik $3$.

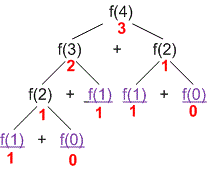
Bu addım-addım proses rekursiv funksiyaların necə işlədiyini göstərir, problemi daha kiçik alt problemlərə bölərək baza hallara çatana qədər və sonra nəticələri birləşdirərək orijinal problemi həll edir. Və gördüyümüz kimi, baza hallar rekursiyanı dayandırmaq və hesablamanın başlanğıc nöqtələrini təmin etmək üçün həlledici rol oynayır.

Çağırış yığımı və onun rekursiv funksiya çağırışlarında necə istifadə edildiyini müzakirə edin

İndi çağırış yığımı anlayışını və onun rekursiv funksiya çağırışlarında necə istifadə edildiyini müzakirə edək. Çağırış yığımını (call stack) yeməkxanadakı boşqab yığını kimi təsəvvür edin. Yeməkxanaya daxil olduqda, bir boşqab götürürsünüz və onu yığının üstünə əlavə edirsiniz. Eyni şəkildə, proqramda bir funksiya çağırıldığında, o funksiya çağırışı haqqında məlumat çağırış yığımına əlavə edilir.

Gəlin bu işin necə getdiyini rekursiv funksiya çağırışları ilə görək:

Funksiya Çağırışları və Çağırış Yığımı:

• Bir funksiya çağırıldığında, çağırış yığımının üstünə həmin funksiya çağırışı haqqında məlumatı saxlamaq üçün yeni bir frame yaradılır. Bu, funksiyanın parametrləri, yerli dəyişənlər və geri dönmə ünvanı - funksiyanın çağırıldıqdan sonra proqramın icrasının davam edəcəyi nöqtəni əhatə edir.

• Hər dəfə yeni bir funksiya çağırıldığında (istər rekursiv, istərsə də adi funksiya çağırışı olsun), çağırış yığımının üstünə yeni bir frame əlavə edilir.

Rekursiv Funksiya Çağırışları:

• Rekursiv funksiya çağırışlarında, funksiya öz bədəni daxilində özünü çağırır. Bu o deməkdir ki, hər rekursiv çağırış çağırış yığımının üstünə yeni bir frame yaradır.

• Rekursiya irəlilədikcə, daha çox frame çağırış yığımına əlavə edilir, hər biri ayrı-ayrı funksiya çağırışını təmsil edir.

• Çağırış yığını bütün bu funksiya çağırışlarını izləyir, proqramın hər funksiya çağırışından sonra haraya qayıtmalı olduğunu təmin edir.

Baza Hali və Yığımın Geri Açılması:

• Nəhayət, rekursiya irəlilədikcə, baza halına çatır. Bu, rekursiyanın sonsuz şəkildə davam etməsinin qarşısını alan dayanma şərtidir.

• Baza halına çatıldığında, funksiya əlavə rekursiv çağırışlar etməyi dayandırır və çağırış yığımı "geri açılmağa" başlayır.

• Hər frame çağırış yığımından çıxarılır və proqram funksiya çağırışının başlanğıc nöqtəsinə qayıdır. Bu proses bütün çağırış yığımı açılana qədər davam edir.

Yaddaş Məsələləri:

• Çağırış yığımı məhdud ölçüyə malikdir və həddindən artıq rekursiya yığımı çox dərin olarsa stack overflow error (çağırış yığımı daşması xətası) ilə nəticələnə bilər.

• Buna görə də, rekursiv funksiyalar yazarkən, sonsuz rekursiyanın qarşısını almaq üçün düzgün baza halının olmasını təmin etmək və yığma daşmasının qarşısını almaq üçün rekursiyanın dərinliyini məhdudlaşdırmaq vacibdir.

Yekun olaraq, çağırış yığımı funksiya çağırışlarını, o cümlədən rekursiv funksiya çağırışlarını idarə etməkdə mühüm rol oynayır. O, funksiya çağırışlarının ardıcıllığını izləyir və proqramın hər bir funksiya çağırışından sonra haraya qayıtmalı olduğunu təmin edir. Çağırış yığımını başa düşmək rekursiyanın necə işlədiyini anlamaq və effektiv və xətasız rekursiv funksiyalar yazmaq üçün vacibdir.

Sonsuz rekursiya anlayışını və ondan necə qaçınmağı izah edin

İndi sonsuz rekursiya anlayışını aydınlaşdırıb və ondan necə qaçınmaq yollarını müzakirə edək.

Sonsuz Rekursiya:

• Sonsuz rekursiya, rekursiv funksiyanın baza halına çatmadan özünü sonsuz şəkildə çağırdığı zaman baş verir.

• Başqa sözlə, funksiya baza halına doğru irəliləmədən özünü təkrar çağırmağa davam edir, nəticədə funksion çağırışlarının sonsuz dövrü yaranır.

• Bu tez bir zamanda mövcud sistem resurslarını tükədir və proqramın çökməsinə və ya sonsuz şəkildə işləməsinə səbəb ola bilər.

Necə Baş Verir:

• Sonsuz rekursiya adətən rekursiv funksiyada düzgün baza halının olmadığında və ya baza halının yanlış olduğunda baş verir.

• Düzgün baza halı və ya baza halına çatmayan yanlış məntiq olmadan funksiya özünü sonsuz şəkildə çağırmağa davam edər.

Nümunə:

Sadə bir nümunə ilə geri sayma funksiyasını nəzərdən keçirək:

def countDown(n):
  # Print current number
  print(n)
  # Call countDown function with the next smaller number
  countDown(n - 1)

# Example usage:
countDown(5)  # Prints numbers from 5 down to minus infinity

Bu halda, rekursiyanı dayandırmaq üçün baza halı yoxdur, buna görə də funksiya $n$-in daha kiçik dəyəri ilə özünü çağırmağa davam edəcək, nəticədə sonsuz rekursiya yaranacaq.

Sonsuz Rekursiyadan Necə Qaçmaq Olar:

• Sonsuz rekursiyadan qaçmaq üçün, hər rekursiv funksiyanın düzgün baza halına malik olduğunu təmin etmək çox vacibdir.

• Baza halı, funksiyanın daha rekursiv çağırışlar etməyi dayandırdığı və nəticəni qaytardığı bir şərt olmalıdır.

• Rekursiv funksiya yazarkən, hər zaman özünüzdən soruşun: "Funksiyanın dayanmasına və nəticəni qaytarmasına səbəb olacaq hansı şərt var?"

• Baza halının əldə olunacağına əmin olun və rekursiv çağırışların ona doğru aparacağını təmin edin.

Düzəldilmiş Nümunə:

• Əvvəlki nümunəni $n$ $0$ olduqda rekursiyanı dayandıran baza halı əlavə edərək düzəldək:

def countDown(n):
  # Base case
  if n == 0: return
  # Print current number
  print(n)
  # Call countDown function with the next smaller number
  countDown(n - 1)

# Example usage:
countDown(5)  # Prints numbers from 5 down to 1

• İndi funksiya $n$ $0$-a çatdıqda özünü çağırmağı dayandıracaq və sonsuz rekursiyadan qaçacaq.

Nəticə olaraq, sonsuz rekursiya rekursiv funksiyanın baza halına çatmadan özünü sonsuz şəkildə çağırdığı zaman baş verir. Ondan qaçmaq üçün, rekursiv funksiyalarınızın rekursiyanı dayandıran və nəticəni qaytaran düzgün baza halına malik olduğunu təmin edin. Fərqli giriş dəyərləri ilə rekursiv funksiyalarınızı test etmək inkişaf zamanı potensial sonsuz rekursiya hallarını tutmağa kömək edə bilər.

Rekursiv Alqoritmlərin Tətbiqi

Rekursiya üçün uyğun proqramlaşdırma problemləri təqdim edin

Gəlin yaxşı tanınan rekursiv alqoritmlər haqqında danışaq.

Problemi $O(n)$ mürəkkəblikli alqoritmdən istifadə edərək həll edə bilərik. Sadə bir for döngüsü yaza bilərik:

# Read the input data
x, n, m = map(int,input().split())

# Initializes a variable res to 1.
# This variable will store the result of x^n mod m
res = 1

# compute the value x^n mod m using n multiplications 
# 1 * x * x * ... * x
for i in range(1,n+1):
  res = (res * x) % m

# print the answer
print(res)

Bu proqram Vaxt Limitini aşır. $n\le 10^9$ olduğundan və bu problemin vaxt limiti sadəcə $1$ saniyə olduğundan, müasir kompüterlərdən istifadə edərək $1$ saniyə ərzində $10^9$ əməliyyatı yerinə yetirə bilməzsiniz.

Çoxaltma prosesini necə sürətləndirə bilərik? Məsələn, $x^{100}$ hesablamaq istəyiriksə, onu $(x^2{)}^{50}$ olaraq bölə bilərik. $x^2$ hesablamaq üçün sadəcə bir vurma istifadə edərək, qüvvəti yarıya qədər azalda bilərik: $100$-dən $50$-ə.

Məsələn, $x^{16}$ tapmaq üçün $16$ vurmadan istifadə etmək əvəzinə, ifadəni belə yenidən yaza bilərik: $x^{16}=(((x^2{)}^2{)}^2{)}^2$, beləliklə sadəcə $4$ vurma həyata keçiririk. Eyni şəkildə, $x^{1024}$ tapmaq üçün sadəcə $10$ vurma yerinə yetirilməlidir.

Əgər qüvvət təkdirsə, məsələn, $n=99$, $x^{99}$ dəyərini $x\cdot x^{98}$ kimi hesablaya bilərik.

Məsələn, $x^{15}=((x^2\cdot x{)}^2\cdot x{)}^2\cdot x$.

Bu da ikilik eksponentasiya metodu, böyük rəqəmlərin qüvvətlərini effektiv şəkildə hesablamaq üçün istifadə edilən bir texnikadır. O, hər hansı bir rəqəmin qüvvətinin $2$ qüvvətlərinin ardıcıllığı kimi ifadə edilə biləcəyi prinsipinə əsaslanır.

Verilən baza $x$ və eksponent $n$ ilə, $n$-i $2$ qüvvətlərinin cəmi kimi ifadə edirik. Məsələn, əgər $n=13$, onu $13=8+4+1$ kimi yaza bilərik. Sonra $x^n$-i hər bir $2$ qüvvətinə yüksəldilmiş $x$ dəyərlərini toplayaraq hesablaya bilərik.

Gəlin $x^{13}$ hesablamaq istəyirik.

• $13$-ü ikilikdə ifadə edək: $13=1101$ ikilik nümayəndəliyində.

• Sonra $x^1$, $x^4$ və $x^8$ (bu $13$-ün ikilik nümayəndəliyindəki dəstək bitlərinə uyğun gəlir) hesablayırıq.

• Nəhayət, bu dəyərləri birləşdirərək çoxaldırıq: $x^{13}=x^1\cdot x^4\cdot x^8$.

Üstünlüklər. İkilik eksponentasiya sadə eksponentasiyaya nisbətən tələb olunan vurmaların sayını azaldır. Xüsusilə böyük eksponentlər üçün effektivdir, çünki $O(n)$ vurmalar əvəzinə sadəcə $O(lo{g}_{2}n)$ vurma tələb edir.

$x^{n}modm$ dəyərini tapmaq üçün aşağıdakı formulu istifadə edəcəyik:

# The myPow function  finds the value of x^n mod m
def myPow(x, n, m):
  if (n == 0): return 1
  if (n % 2 == 0): return myPow((x * x) % m, n / 2, m)
  return (x * myPow(x, n - 1, m)) % m

# The main part of the program. Read the input data
x, n, m = map(int, input().split())

# Compute and print the answer
print(myPow(x, n, m))

Python-da $x^{n}modm$ hesablamaq üçün $pow(x,n,m)$ adlı daxili funksiya var. Əvvəlki kodu aşağıdakı kimi yenidən yaza bilərik:

# Read the input data
x, n, m = map(int, input().split())

# Compute and print the answer
print(pow(x, n, m))

İki tam ədədin Böyük Ortaq Böləni (GCD) $a$ və $b$, hər iki rəqəmi də qalıqsız bölən ən böyük müsbət tam ədəddir.

Nümunə:

• Gəlin iki tam ədədi götürək, $a=12$ və $b=18$.

• $12$-nin bölənləri $1,2,3,4,6$ və $12$-dir.

• $18$-in bölənləri $1,2,3,6,9$ və $18$-dir.

• $12$ və $18$-in ortaq bölənləri $1,2,3$ və $6$-dır.

• Bu ortaq bölənlərdən ən böyüyü $6$-dır.

• Buna görə də, $gcd(12,18)=6$.

Xüsusiyyətlər:

• GCD həmişə müsbət tam ədəddir.

• Əgər $a$ və $b$ hər ikisi sıfırdırsa, $gcd(a,b)=0$.

• Əgər $a$ və ya $b$ (və ya hər ikisi) mənfidirsə, $gcd(a,b)$ onların mütləq qiymətlərinin GCD-si ilə eynidir.

• Əgər $a$ və ya $b$ sıfırdırsa, $gcd(a,b)$ sıfır olmayan ədədin mütləq dəyəridir.

• Hər hansı bir rəqəmlə $0$-ın GCD-si həmin rəqəmin öz mütləq dəyəridir.

Tətbiqlər:

• GCD müxtəlif riyazi hesablamalarda, o cümlədən fraksiyaların sadələşdirilməsində və ən azı ümumi böləni tapmaqda istifadə olunur.

• O, RSA kimi kriptoqrafik alqoritmlərdə açar yaratmaq və şifrələmək üçün istifadə olunur.

• O, kompüter elmləri alqoritmlərində, məsələn, iki rəqəmin GCD-sini effektiv şəkildə tapmaq üçün istifadə olunan Evklid alqoritmində istifadə olunur.

Evklid alqoritmi iki tam ədədin GCD-sini tapmaq üçün effektiv bir metoddur. Bu, bir neçə dəfə böyük ədəddən kiçik ədəd çıxarmaqla iki rəqəmin GCD-nin dəyişməz qaldığı prinsipinə əsaslanır.

"Minus" əməliyyatı əvəzinə "mod" əməliyyatından istifadə etsək, hesablamalar daha sürətli olacaq.

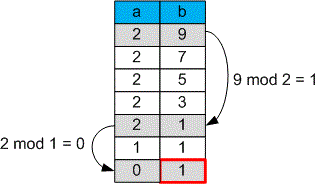
Məsələn, $GCD(1,10^9)$ tapmaq üçün çıxarışdan istifadə edərək $10^9$ əməliyyat yerinə yetirilməlidir. Bununla belə, mod əməliyyatından istifadə edərkən yalnız bir hərəkət kifayətdir.

Verilən iki tam ədəd $a$ və $b$, burada $a\ge b$, aşağıdakı addımları təkrarlayaraq yerinə yetiririk:

• Əgər $b$ sıfırdırsa, GCD $a$-dır.

• Əks halda, $a$-nı $b$ ilə, $b$-ni isə $a$-nın $b$ ilə bölünəndə qalanı ilə əvəz edirik. Bu, $a\leftarrow b$ və $b\leftarrow amodb$ kimi ifadə edilə bilər.

• Bu prosesi $b$ sıfır olana qədər davam etdiririk.

$a$ və $b$-nin GCD-si $b$ sıfır olduqda $a$-nın dəyəridir.

Evklid alqoritmi effektivdir və $O(lo{g}_{2}min(a,b))$ vaxt mürəkkəbliyinə malikdir. Bu, zəmanətli olaraq sona çatır, çünki $b$-nin dəyəri hər iterasiya ilə azalır və nəticədə $b$ sıfır olur.

İki rəqəmin GCD-sini aşağıdakı formula istifadə edərək tapmaq olar:

def gcd(a, b):
  if a == 0: return b
  if b == 0: return a
  if a > b: return gcd(a % b, b)
  return gcd(a, b % a)

# The main part of the program. Read the input data. 
a, b = map(int, input().split())

# Find and print the GCD of two numbers.
print(gcd(a, b))

Verilən formula başqa bir formada ifadə edilə bilər:

def gcd(a, b):
  if b == 0: return a
  return gcd(b, a % b)

# The main part of the program. Read the input data.
a, b = map(int, input().split())

# Find and print the GCD of two numbers.
print(gcd(a, b))

Python-da iki rəqəmin Böyük Ortaq Bölənini hesablamaq üçün $gcd(a,b)$ adlı daxili funksiya var. Əvvəlki kodu aşağıdakı kimi yenidən yaza bilərik:

import math

#  Read the input data.
a, b = map(int, input().split())

# Find and print the GCD of two numbers.
print(math.gcd(a, b))

Problemlər siyahısı

Rekursiv proqramlar:

• 1603. Rəqəmlərin cəmi

• 1658. Faktorial (dərsdə istifadə edilmişdir)

• 2999. Funksiya – 10

• 8609. Rekursiya – 1

• 11249. Rekursiya – 2

Fibonacci nömrələri:

• 3258. Fibonacci ardıcıllığı (dərsdə istifadə edilmişdir)

• 8295. Fibonacci sıra nəsli

GCD / LCM:

• 136. Segment

• 1601. İki rəqəmin GCD-si (dərsdə istifadə edilmişdir)

• 1602. İki tam ədədin LCM-si

• 2214. Funksiya 9

• 7363. Fraksiyaların cəmi

Binomial əmsal:

• 3260. Nə qədər?

Eksponentasiya:

• 273. Modulyar eksponentasiya

• 5198. Modulyar eksponentasiya (dərsdə istifadə edilmişdir)

• 9644. Qüvvətlərin cəmi

• 9646. Qüvvətlərin cəmi 2