Redaksiya

Сonstruct a $0-1$ graph by assigning a weight of $0$ to the existing edges and a weight of $1$ to their reversed edges. Then, run a breadth-first search. The length of the shortest path from vertex $1$ to vertex $n$ will equal the minimum number of edges that need to be reversed.

Example

The graph in the example looks as follows:

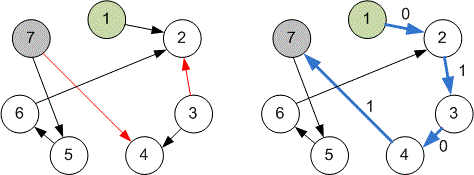
Algorithm realization

Declare the constant infinity.

#define INF 0x3F3F3F3F

Declare the array of shortest distances $dist$ and the adjacency list of the graph $g$. For each edge, store its weight ($0$ or $1$) along with the adjacent vertex.

vector<int> dist;
vector<vector<pair<int, int> > > g;

The bfs function implements breadth-first search from the vertex $start$.

void bfs(int start)
{
  dist = vector<int>(n + 1, INF);
  dist[start] = 0;

  deque<int> q;
  q.push_back(start);

  while (!q.empty())
  {
    int v = q.front(); q.pop_front();
    for (auto edge : g[v])
    {
      int to = edge.first;
      int w = edge.second;
      if (dist[to] > dist[v] + w)
      {
        dist[to] = dist[v] + w;

Depending on the weight of the edge $w$, add vertex $to$ to the end or the front of the queue.

        if (w == 1)
          q.push_back(to);
        else
          q.push_front(to);
      }
    }
  }
}

The main part of the program. Read the input data.

scanf("%d %d", &n, &m);
g.resize(n + 1);
for (i = 0; i < m; i++)
{
  scanf("%d %d", &a, &b);

Assign a weight of $0$ to a directed edge $a\to b$, and a weight of $1$ to the reverse edge.

  g[a].push_back({ b, 0 });
  g[b].push_back({ a, 1 });
}

Start the breadth-first search from the vertex $1$.

bfs(1);

Print the answer — the shortest distance to vertex $n$.

if (dist[n] == INF)
  printf("-1\n");
else
  printf("%d\n", dist[n]);