Redaksiya

Let the array $m$ contain the cutting points: $m_1,...,m_n$. Add the start and end points: $m_0=0$ and $m_{n+1}=l$.

Let the function $f(a,b)$ return the minimal cost of cutting a stick from $m_a$ to $m_b$ considering the necessary cutting points within the segment. There are no cutting points within the segment $[m_a;m_{a+1}]$, so $f(a,a+1)=0$. The solution to the problem will be the value of $f(0,n+1)$. Store the computed values of $f(a,b)$ in the cells of the array $dp[a][b]$.

Let the segment of the stick $[m_a,m_b]$ be cut into several pieces. If the first cut is made at point $m_i(a<i<b)$, the cost of the cut itself will be $m_b-m_a$. Then, the remaining pieces need to be cut at the costs $f(a,i)$ and $f(i,b)$, respectively. Choose $i$ to minimize the total cost:

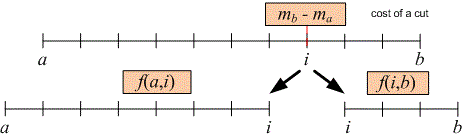
Example

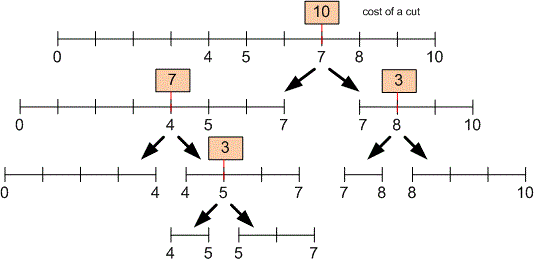
Consider the second test case. Here is one possible way to cut a stick of length $10$ with a cost of $10+7+3+3=23$:

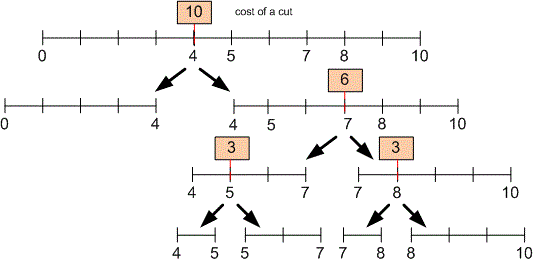
Now, consider the optimal way to cut the stick, which has a cost of $10+6+3+3=22$:

Algorithm implementation

Declare constants and arrays.

#define MAX 55
#define INF 0x3F3F3F3F
int dp[MAX][MAX];
int m[MAX];

The function $f(a,b)$ returns the minimum cost of cutting a piece of stick on the segment $[a;b]$ at the cutting points located inside the segment.

int f(int a, int b)
{

If $a+1=b$, then there are no cutting points within the segment $[a;b]$. Return $0$.

  if (b - a == 1) return 0;

If the value of $f(a,b)$ is already computed, return it.

  if (dp[a][b] != INF) return dp[a][b];

Make a cut at the point $i(a<i<b)$. Compute the cost as follows:

  for (int i = a + 1; i < b; i++)
    dp[a][b] = min(dp[a][b], m[b] - m[a] + f(a, i) + f(i, b));

Return the result $f(a,b)=dp[a][b]$.

  return dp[a][b];
}

The main part of the program. Read the input data for each test case.

while(scanf("%d",&l),l)
{
  scanf("%d",&n);

Add the start and end cutting points: $m_0=0,m_{n+1}=l$.

  m[0] = 0; m[n+1] = l;
  for(i = 1; i <= n; i++)
    scanf("%d",&m[i]);

Initialize the $dp$ array.

  memset(dp,0x3F,sizeof(dp));

Find and print the answer.

  printf("The minimum cutting is %d.\n",f(0,n+1));
}