Redaksiya

The interval $A[i...j]$ will be called good if the numbers in it lie in the range $[A_i;2\cdot A_i]$ inclusive (meaning $A_j\le 2\cdot A_i$).

We implement a sliding window using two pointers $i$ and $j$ and maintain it so that the current interval $[i...j]$ is good, while the interval $[i...j+1]$ is bad.

For example, for the following sequence:

• the intervals $[2;2],[2;3],[2;4]$, and $[2;5]$ are good.

• the intervals $[2;6],[2;7]$ are bad.

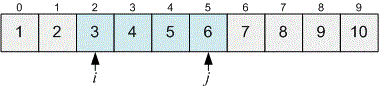
If $A_j\le 2\cdot A_i$, extend the current interval to $А[i...j+1]$. Otherwise, reduce it to $А[i+\mathrm{1...}j]$. Before moving the pointer $i$, print the number of elements lying between $A_i$ and $2\cdot A_i$ inclusive. It equals $j-i$.

The algorithm’s complexity is linear, i.e. $O(n)$.

Example

Let’s consider the movement of pointers for the given example.

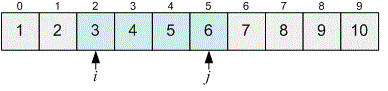
For the given condition $A_j\le 2\cdot A_i$, so we move the pointer $j$ forward.

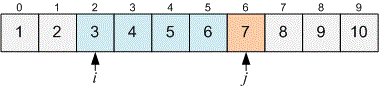
Now $A_j>2\cdot A_i$. We need to move the pointer $i$ forward. However, before moving it, print the number of elements lying between $A_i$ and $2\cdot A_i$ inclusive. It is equal to $j-i=6-2=4$.

Move $j$ forward until $A_j\le 2\cdot A_i$.

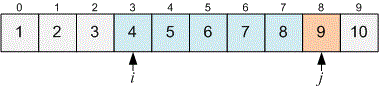
Now $A_j>2\cdot A_i$. Print the answer for $i=3$ (it equals $j-i=8-3=5$) and increase $i$ by $1$.

Algorithm realization

Read the input data.

scanf("%d", &n);
for (i = 0; i < n; i++)
  scanf("%d", &a[i]);

Initialize the pointers $i=j=0$.

i = j = 0;

Move the pointers forward until an answer is found for each value of $i<n$.

while (i < n) // [i..j]
{

If $A_j\le 2\cdot A_i$ (and $j$ has not exceeded the array bounds, meaning $j<n$), extend the current interval by incrementing the pointer $j$.

  if ((j < n) && (a[j] <= 2 * a[i])) j++;
  else
  {

If $A_j>2\cdot A_i$, print the answer for index $i$ and increment $i$ by one.

    printf("%d ", j - i);
    i++;
  }
}

Algorithm realization — binary search, O(n log n)

Read the input data.

scanf("%d", &n);
v.resize(n);
for (i = 0; i < n; i++)
  scanf("%d", &v[i]);

For each index $i<n$, using binary search, find the largest value of the index $x$ such that the numbers from $A_i$ to $2\cdot A_i$ are contained in the interval $[i;x-1]$, and $A_x>2\cdot A_i$. The count of numbers in the interval $[i;x-1]$ equals $x-i$.

for (i = 0; i < n; i++)
{
  x = upper_bound(v.begin(), v.end(), 2 * v[i]) - v.begin();
  printf("%d ", x - i);
}

Java realization

import java.util.*;
 
public class Main
{
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    int n = con.nextInt();
    int m[] = new int[n];
    for(int i = 0; i < n; i++)
      m[i] = con.nextInt();

    int i = 0, j = 0;
    while (i < n) // [i..j]
    {
      if ((j < n) && (m[j] <= 2 * m[i])) j++;
      else
      {
        System.out.print(j - i + " ");
        i++;
      }
    }

    con.close();
  }
}

Python realization

Read the input data.

n = int(input())
lst = list(map(int,input().split()))

Initialize the pointers $i=j=0$.

i = j = 0

Move the pointers forward until an answer is found for each value of $i<n$.

while (i < n): # [i..j]

If $A_j\le 2\cdot A_i$ (and $j$ has not exceeded the array bounds, meaning $j<n$), extend the current interval by incrementing the pointer $j$.

  if (j < n and lst[j] <= 2 * lst[i]):
    j += 1
  else:

If $A_j>2\cdot A_i$, print the answer for index $i$ and increment $i$ by one.

    print(j - i, end=" ");
    i += 1

Python realization — binary search, O(n log n)

from bisect import bisect_right

Read the input data.

n = int(input())
v = list(map(int, input().split()))

For each index $i<n$, using binary search, find the largest value of the index $x$ such that the numbers from $A_i$ to $2\cdot A_i$ are contained in the interval $[i;x-1]$, and $A_x>2\cdot A_i$. The count of numbers in the interval $[i;x-1]$ equals $x-i$.

for i in range(n):
  x = bisect_right(v, 2 * v[i])
  print(x - i, end=" ")