İnteqral Düzbucaqlılar
Gəlin hündürlüyü h və eni w olan, hər ikisi tam ədəd olan düzbucaqlıları nəzərdən keçirək. Belə düzbucaqlılara tam düzbucaqlılar deyirik. Bu məsələdə yalnız geniş tam düzbucaqlıların üzərində dayanırıq, yəni w > h olanları.
Geniş tam düzbucaqlıların sıralanması aşağıdakı qaydada müəyyən edilir. İki geniş tam düzbucaqlı verildikdə,
Diaqonal xətti daha qısa olan kiçik hesab edilir və
Əgər hər iki düzbucaqlının diaqonal xətləri eyni uzunluqdadırsa, hündürlüyü daha qısa olan kiçik hesab edilir.
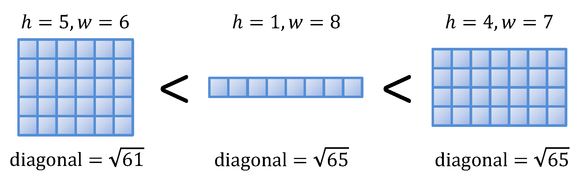
Verilmiş geniş tam düzbucaqlıdan daha böyük olan ən kiçik geniş tam düzbucaqlını tapın.
Giriş verilənləri
Giriş bir neçə məlumat dəstindən ibarətdir. Məlumat dəstlərinin sayı 100-dən çox deyil. Hər bir məlumat dəsti geniş tam düzbucaqlını onun hündürlüyü və eni, yəni h və w, bir sətirdə boşluqla ayrılmış şəkildə təsvir edir.
h w
Hər bir məlumat dəsti üçün h və w (> h) hər ikisi 0-dan böyük və 100-dən çox olmayan tam ədədlərdir.
Girişin sonu boşluqla ayrılmış iki sıfırdan ibarət bir sətirlə göstərilir.
Çıxış verilənləri
Hər bir məlumat dəsti üçün verilmiş düzbucaqlıdan daha böyük olan ən kiçik geniş tam düzbucaqlının hündürlüyü və eni, yəni h və w (> h), təsvir edən iki ədədi bir sətirdə çap edin. Ədədlərin arasında boşluq qoyun. Çıxışda başqa simvollar icazə verilmir.
Girişdə verilmiş hər hansı geniş tam düzbucaqlı üçün, verilmiş düzbucaqlıdan daha böyük olan ən kiçik geniş tam düzbucaqlının eni və hündürlüyü hər ikisi 150-dən çox olmadığı məlumdur.
Bundan əlavə, geniş tam düzbucaqlıların sıralanması diaqonal xətlərin uzunluqlarının müqayisəsi ilə istifadə edilsə də, bu müqayisə diaqonal xətlərin uzunluqlarının kvadratlarının (öz-özünə vurulmuş) müqayisəsi ilə əvəz edilə bilər ki, bu da ehtimal olunan üzən nöqtəli ədədlərin istifadəsi ilə yaranan lazımsız problemlərdən qaçınmağa imkan verir.