Metro

Alqoritmin Təhlili

Mənbədən $v$ təpəsinə, $l$ xəttinə aid olan ən qısa məsafə dist[v][l]-də saxlanılır, burada $1 \leq v \leq 70, 1 \leq l \leq 10$ . Qraf kimi qonşuluq siyahıları kimi saxlanılır. Yön və kənarın qiyməti ilə birlikdə, kənarın yönəldiyi təpəyə aid olan metro xəttinin nömrəsi də saxlanılır.

Biz $s$ stansiyasından, $l in e 1$ xəttindən başlayırıq. Problemin cavabı $f$ təpəsinə, $l in e 2$ xəttinə ən az xərclə ilə çatmaqdır. Təpələr arasında hərəkət edərkən, yoxlama aparılmalıdır: əgər təpələr müxtəlif xətlərə aiddirsə, onda 1 əlavə edilməlidir (keçid etmək üçün).

Dijkstra alqoritmi ilə ( $s$ , $l in e 1$ ) vəziyyətindən ( $f$ , $l in e 2$ ) vəziyyətinə ən qısa məsafələri tapırıq.

Nümunə

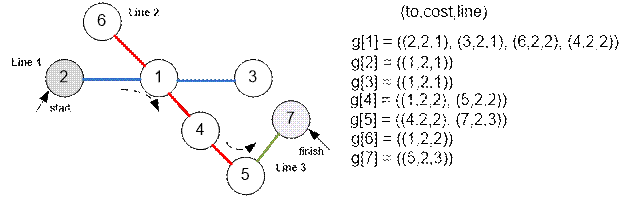
Nümunədə təqdim edilmiş qraf belə görünür:

2 nömrəli stansiyadan 7 nömrəli stansiyaya getmək üçün 4 seqment (8 dəqiqə) və 2 keçid (2 dəqiqə) etmək lazımdır. Ümumi səyahət müddəti 10 dəqiqə çəkəcək.

Alqoritmin Tətbiqi

Qrafda olan təpələrin sayı MAX = 71-dən çox deyil. Xətlərin sayı LINES = 11-dən çox deyil.

#define MAX 71
#define LINES 11

int dist[MAX][LINES];

struct node
{
    int to, cost, line;
    node(int to, int cost, int line) : to(to), cost(cost), line(line) {}
};

bool operator< (node a, node b)
{
    return a.cost > b.cost;
}

vector<vector<node>> g;

// Giriş məlumatlarını oxumaq və qrafı başlatmaq

for (i = 1; i <= l; i++)
{
    scanf("%d ", &u);
    while (scanf("%d%c", &v, &ch))
    {
        g[u].push_back(node(v, 2, i));
        g[v].push_back(node(u, 2, i));
        u = v;
        if (ch == '\n') break;
    }
}

// Ən qısa məsafələr massivini başlatmaq
for (i = 1; i <= n; i++)
    for (j = 1; j <= l; j++)
        dist[i][j] = 2000000000;

// Başlanğıc və son stansiyalar haqqında məlumatı oxumaq
scanf("%d %d %d %d", &s, &line1, &f, &line2);

// Dijkstra alqoritmi
dist[s][line1] = 0;
priority_queue<node, vector<node>> pq;
pq.push(node(s, 0, line1)); // (v, cost, line)

while (!pq.empty())
{
    int cost = pq.top().cost;
    int v = pq.top().to;
    int l1 = pq.top().line;
    pq.pop();

    for (i = 0; i < g[v].size(); i++)
    {
        int to = g[v][i].to;
        int w = g[v][i].cost;
        int l2 = g[v][i].line;
        int tot_cost = cost + w;
        if (l1 != l2) tot_cost += 1;
        if (tot_cost < dist[to][l2])
        {
            dist[to][l2] = tot_cost;
            pq.push(node(to, tot_cost, l2));
        }
    }
}

// Cavabı çıxartmaq
printf("%d\n", dist[f][line2]);