Editorial

Consider a tree with $n$ vertices.

A centroid of a tree is a vertex whose removal results in splitting the tree into connected components, each containing no more than $n /2$ vertices.

The task is to find all centroids of the tree.

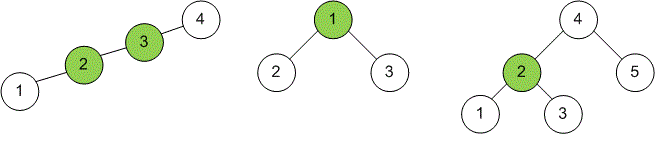
Let’s consider examples of trees and their centroids (marked in green).

Run a depth-first search starting from vertex $v$ , which will calculate the number of vertices in the subtree rooted at vertex $v$ and store this value in $s u b [v]$ . For the given examples, we will indicate the corresponding value of $s u b [v]$ next to each vertex $v$ . In all examples, the depth-first search starts from vertex $1$ .

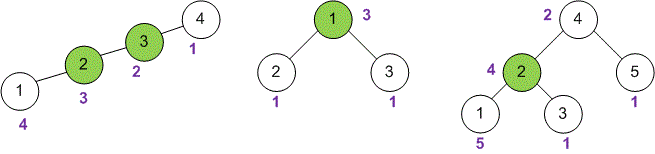
If vertex $v$ has children $t o_{1}, t o_{2}, ..., t o_{k}$ , then

s u b_{v} = 1 + s u b_{t o_{1}} + s u b_{t o_{2}} + ... + s u b_{t o_{k}}

Vertex $v$ is a centroid of the tree if and only if:

for each of its children $t o$ , it holds that $s u b [t o] \leq n /2$ ;
if we remove the subtree rooted at $v$ from the tree, the resulting tree contains no more than $n /2$ vertices: $n - s u b [v] \leq n /2$ ;

For example, in the tree from the right with $n = 5$ vertices, vertex $2$ is a centroid because:

$s u b [4] = 2 \leq n /2$ ;
$s u b [3] = 1 \leq n /2$ ;
$n - s u b [2] = 5 - 4 = 1 \leq n /2$ ;

Example

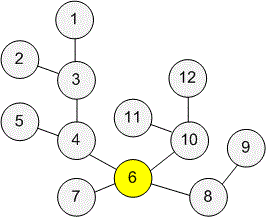
Let's consider the tree from the example. Vertex $6$ is a centroid.

Algorithm realization

We’ll store the graph in the adjacency list $g$ .

vector<vector<int> > g;

The dfs function returns the number of vertices in the subtree rooted at vertex $v$ and saves this value in $s u b [v]$ .

int dfs(int v, int p = -1)
{
  sub[v] = 1;
  for (int to : g[v])
    if (to != p) sub[v] += dfs(to, v);
  return sub[v];
}

The centroid function performs a depth-first search, finds the centroids, and stores them in the $ce n t r$ array.

void centroid(int v, int p = -1)
{

Set $f l a g = 1$ if vertex $v$ is a centroid.

  int flag = 1;

Iterate through the vertices $t o$ , adjacent to $v$ . Consider an edge $v \to t o$ .

  for (int to : g[v])
    if (to != p)
    {

If for a child $t o$ it holds that $s u b [t o] > n /2$ , then $v$ is not a centroid.

      if (sub[to] > n / 2) flag = 0;

If for a child $t o$ it holds that $s u b [t o] < n /2$ , then the subtree rooted at $t o$ does not contain centroids. It makes sense to continue the search in the child $t o$ only if $s u b [t o] \geq n /2$ .

      if (sub[to] >= n / 2) centroid(to, v);
    }

The tree without the subtree rooted at $v$ contains $n - s u b [v]$ vertices. If it contains more than $n /2$ vertices, then $v$ is not a centroid.

  if (n - sub[v] > n / 2) flag = 0;

If vertex $v$ satisfies all the conditions of a centroid, add it to the $ce n t r$ array.

  if (flag) centr.push_back(v);
}

The main part of the program. Read the input data and initialize the arrays.

scanf("%d", &n);
g.resize(n + 1);
sub.resize(n + 1);

Read the input graph.

for (i = 0; i < n - 1; i++)
{
  scanf("%d %d", &a, &b);
  g[a].push_back(b);
  g[b].push_back(a);
}

Run a depth-first search and find the centroids of the tree.

dfs(1);
centroid(1);

Print one of the centroids.

printf("%d\n", centr[0]);

Algorithm realization – second solution

Let’s run a depth-first search $df s (v)$ , that will compute the following values for each vertex $v$ :

$s u b [v]$ contains the number of vertices in the subtree with vertex $v$ ;
$f [v]$ contains the maximum size of a subtree among all subtrees of vertex $v$ , including the subtree containing the parent vertex of $v$ .

Then, the centroid will be the vertex $v$ with the smallest value of $f [v]$ . There may be either one or two such vertices in the tree.

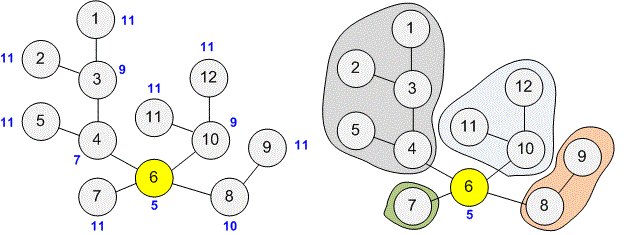
Vertex $v = 6$ is connected to $4$ subtrees, with sizes $1, 2, 3$ and $5$ respectively. The value $f [6] = 5$ contains the maximum size of a subtree.

At the same time, the smallest value in the array $f$ is $f [6] = 5$ . Therefore, vertex $6$ is the centroid.

Let’s consider the labeling of a tree with two centroids.

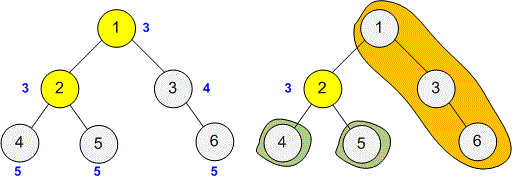
Two vertices have the smallest value in the array $f$ : $f [1] = 3$ and $f [2] = 3$ .

void dfs(int v, int p = -1)
{
  sub[v] = 1;
  f[v] = 0;
  for (int to : g[v])
    if (to != p)
    {
      dfs(to, v);
      sub[v] += sub[to];
      f[v] = max(f[v], sub[to]);
    }
  f[v] = max(f[v], n - sub[v]);
  if ((root == 0) || (f[v] < f[root])) root = v;
}

The main part of the program. Read the input data and initialize the arrays.

scanf("%d", &n);
g.resize(n + 1);
f.resize(n + 1);
sub.resize(n + 1);
for (i = 0; i < n - 1; i++)
{
  scanf("%d %d", &a, &b);
  g[a].push_back(b);
  g[b].push_back(a);
}

Run a depth-first search and print one of the centroids $roo t$ of the tree.

root = 0;
dfs(1);
printf("%d\n", root);

Python realization

Increase the size of the stack.

import sys
sys.setrecursionlimit(300000)

The dfs function returns the number of vertices in the subtree rooted at vertex $v$ and saves this value in $s u b [v]$ .

def dfs(v, p = -1):
  sub[v] = 1
  for to in g[v]:
    if to != p:
      sub[v] += dfs(to, v)
  return sub[v]

The centroid function performs a depth-first search, finds the centroids, and stores them in the $ce n t r$ array.

def find_centroid(v, p = -1):

Set $f l a g = T r u e$ if vertex $v$ is a centroid.

  flag = True

Iterate through the vertices $t o$ , adjacent to $v$ . Consider an edge $v \to t o$ .

  for to in g[v]:
    if to == p: continue

If for a child $t o$ it holds that $s u b [t o] > n /2$ , then $v$ is not a centroid.

    if sub[to] > n // 2:
      flag = False

    if sub[to] >= n // 2:
      find_centroid(to, v)

The tree without the subtree rooted at $v$ contains $n - s u b [v]$ vertices. If it contains more than $n /2$ vertices, then $v$ is not a centroid.

  if n - sub[v] > n // 2:
      flag = False

If vertex $v$ satisfies all the conditions of a centroid, add it to the $ce n t r$ array.

  if flag: centr.append(v)

The main part of the program. Read the input data and initialize the arrays.

n = int(input())
g = [[] for _ in range(n + 1)]
sub = [0] * (n + 1)
centr = []

Read the input graph.

for i in range(n - 1):
  a, b = map(int, input().split())
  g[a].append(b)
  g[b].append(a)

Run a depth-first search and find the centroids of the tree.

dfs(1)
find_centroid(1)

Print one of the centroids.

print(centr[0])

Python realization – second solution

Increase the size of the stack.

import sys
sys.setrecursionlimit(200000)

Let’s run a depth-first search $df s (v)$ , that will compute the following values for each vertex $v$ :

$s u b [v]$ contains the number of vertices in the subtree with vertex $v$ ;
$f [v]$ contains the maximum size of a subtree among all subtrees of vertex $v$ , including the subtree containing the parent vertex of $v$ .

Then, the centroid will be the vertex $v$ with the smallest value of $f [v]$ . There may be either one or two such vertices in the tree.

def dfs(v, p=-1):
  global root
  sub[v] = 1
  f[v] = 0
  for to in g[v]:
    if to != p:
      dfs(to, v)
      sub[v] += sub[to]
      f[v] = max(f[v], sub[to])
  f[v] = max(f[v], n - sub[v])
  if root == 0 or f[v] < f[root]:
    root = v

The main part of the program. Read the input data and initialize the arrays.

n = int(input())
g = [[] for _ in range(n + 1)]
f = [0] * (n + 1)
sub = [0] * (n + 1)

for _ in range(n - 1):
  a, b = map(int, input().split())
  g[a].append(b)
  g[b].append(a)

Run a depth-first search and print one of the centroids $roo t$ of the tree.

root = 0
dfs(1)
print(root)