Editorial

For each number $x$ we’ll store the number of times $freq[x]$ that it occurs in the stack. Let’s choose a map as a data structure for $freq$.

Declare an array of stacks vector<stack<int>> st. Here $st[i]$ stores elements that occur on the stack $i+1$ times (the numbering of cells in the st array starts from zero). The order in which the elements are in $st[i]$ matches the order in which they are pushed onto the stack.

Let the number $x$ be pushed to the stack for the $k$-th time. If the element $st[k–1]$ does not exist, then add (push_back) the element to the $st$ array. Then push $x$ to the top of the stack $st[k–1]$.

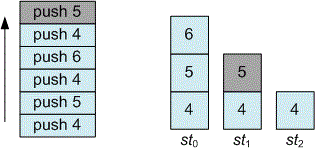
When you delete element, you must pop the item from the top of the last stack.

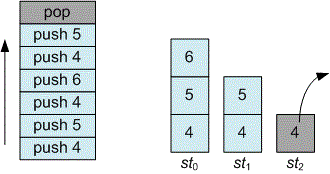
For example, if in the future there are only pop operations, then the elements from the stack will be removed in the following order: $4,5,4,6,5,4$.

Example

Consider the order in which elements are pushed into array of stacks for the next example.

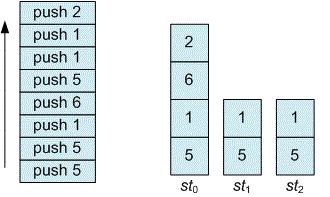
When removed, items will be popped from the stack in the following order: $1,5,1,5,2,6,1,5$.

Algorithm realization

To work with the frequency stack, we declare the FreqStack class.

class FreqStack
{
public:

Declare:

• map $freq$, where $freq[x]$ contains the number of times an element $x$ occurs in the stack

• • array of stacks $st$;

  map<int, int> freq;
  vector<stack<int>> st;

The function push pushes the element $x$ to the stack.

  void push(int x)
  {
    int f = freq[x];
    freq[x] = f + 1;
    if (f == st.size()) st.push_back(stack<int>());
    st[f].push(x);
  }

The function pop pops element from the stack.

  int pop()
  {
    int x = st.back().top();
    st.back().pop();
    if (st.back().empty()) st.pop_back();
    freq[x]--;
    return x;
  }
};

The main part of the program. Read the input data. Simulate the stack.

while (cin >> str)
{
  if (str == "push")
  {
    cin >> n;
    fs.push(n);
  }
  else // pop
    cout << fs.pop() << endl;
}