Editorial

Using depth-first search, compute the XOR sum between vertex $1$ and all other vertices. Store the XOR sum between vertex $1$ and $v$ in $x[v]$. Let $ones$ be the number of ones and $zeroes$ be the number of zeros in the array $x(ones+zeroes=n)$. Then the answer to the problem will be $ones\cdot zeroes$.

Example

Consider the graph provided in the example.

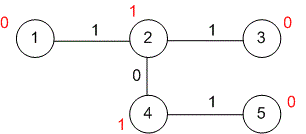
Next to each vertex $v$, the XOR sum $x[v]$ between $1$ and $v$ is written. If $x[v]=x[u]$ for some vertices $v$ and $u$, then the XOR sum between them is equal to $0$, thus contributing $0$ to the total sum. The XOR sum for each pair of vertices $(v,u)$, for which $x[v]\ne x[u]$, contributes $1$ to the total sum.

Therefore, the answer is equal to the number of pairs of vertices $(v,u)$ for which $x[v]\ne x[u]$. This number is equal to $ones\cdot zeroes=2\cdot 3=6$. The pairs of vertices that contribute $1$ to the total sum are: $(1,2),(1,4),(2,3),(2,5),(3,4),(4,5)$.

Algorithm realization

Store the input graph in the adjacency list $g$. Declare an array $x$.

vector<vector<pair<int,int> > > g;
vector<int> x;

The dfs function implements a depth-first search that computes the XOR sum $x[v]$ between vertices $1$ and $v$. The current XOR sum between $1$ and $v$ is represented by $cur\_xor$. The parent of vertex $v$ is $p$.

void dfs(int v, int cur_xor, int p = -1)
{
  x[v] = cur_xor;
  for (auto z : g[v])
  {
    int to = z.first;
    int w = z.second;
    if (to != p) dfs(to, cur_xor ^ w, v);
  }
}

The main part of the program. Read the input graph.

scanf("%d", &n);
g.resize(n + 1);
x.resize(n + 1);

for (i = 1; i < n; i++)
{
  scanf("%d %d %d", &u, &v, &d);
  g[u].push_back(make_pair(v, d));
  g[v].push_back(make_pair(u, d));
}

Start the depth-first search from vertex $1$.

dfs(1, 0, -1);

Compute the number of $zeroes$ and $ones$ in the array $x$.

ones = 0;
for (i = 1; i <= n; i++)
  if (x[i] == 1) ones++;
zeroes = n - ones;

Print the answer.

printf("%lld\n", 1LL * ones * zeroes);

Python realization

The dfs function implements a depth-first search that computes the XOR sum $x[v]$ between vertices $1$ and $v$. The current XOR sum between $1$ and $v$ is represented by $cur\_xor$. The parent of vertex $v$ is $p$.

def dfs(v, cur_xor = 0, p = -1):
  x[v] = cur_xor
  for to, w in g[v]:
    if to != p:
      dfs(to, cur_xor ^ w, v)

The main part of the program. Read the input graph.

n = int(input())
g = [[] for _ in range(n + 1)]
for _ in range(n - 1):
  u, v, d = map(int, input().split())
  g[u].append((v, d))
  g[v].append((u, d))

Initialize the list $x$.

x = [0] * (n + 1)

Start the depth-first search from vertex $1$.

dfs(1)

Compute the number of $zeroes$ and $ones$ in the array $x$.

ones = sum(x)
zeroes = n - ones

Print the answer.

print(ones * zeroes)