Editorial

Let's use the disjoint-set data structure. Initially, each vertex will be placed in a separate set. We will iterate through the edges in decreasing order of their weights. For each edge $(u,v)$, we will run the $Union(u,v)$ function. It will merge the sets containing vertices $u$ and $v$.

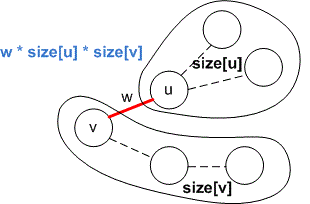
Consider the current edge $(u,v)$ of the tree with weight $w$. Let it merge the sets with sizes $size[u]$ and $size[v]$. All edges in these two sets have weights greater than or equal to $w$. The edge $(u,v)$ is part of $size[u]\cdot size[v]$ different paths. Since the weight $w$ is minimal, the distances of these paths are equal to $w$. Therefore, the contribution of these paths to the sum of distances of all pairs of vertices is $w\cdot size[u]\cdot size[v]$.

Example

Consider the first test.

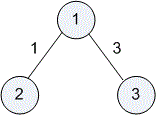
The graph contains three paths:

• $1\to 2$ (distance $1$);

• $1\to 3$ (distance $3$);

• $2\to 1\to 3$ (distance $1$);

The sum of distances between all pairs of vertices is equal to $1+3+1=5$.

Consider the second test.

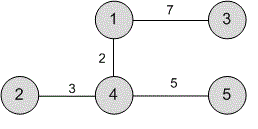
Assign each vertex to a separate set.

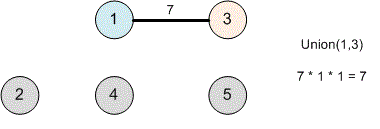
Iterate through the edges in descending order of weight. The first edge will be $(1,3)$. Perform $Union(1,3)$. The distance $7$ has $size[1]\cdot size[3]=1\cdot 1=1$ path (from $1$ to $3$).

The next edge will be $(4,5)$. Perform $Union(4,5)$. The distance $5$ has $size[4]\cdot size[5]=1\cdot 1=1$ path (from $4$ to $5$).

The next edge will be $(2,4)$. Perform $Union(2,4)$. The distance $3$ have $size[2]\cdot size[4]=1\cdot 2=2$ paths (from $2$ to $4$ and from $2$ to $5$).

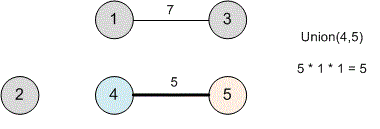
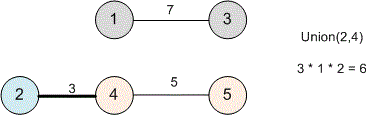
The next edge will be $(1,4)$. Perform $Union(1,4)$. The distance $2$ have $size[1]\cdot size[4]=2\cdot 3=6$ paths $(2\to 4\to 1,4\to 1,5\to 4\to 1,2\to 4\to 1\to 3,4\to 1\to 3,5\to 4\to 1\to 3)$.

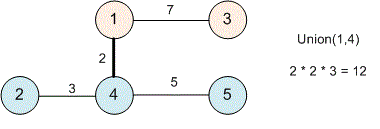
The desired sum of distances is equal to $7+5+6+12=30$.

Algorithm realization

Declare arrays used by the disjoint-set system.

struct Edge
{
  int u, v, cost;
} temp;
vector<Edge> e;
vector<int> parent, ssize;

The cmpGreater function is a comparator that sorts the edges in descending order of weight.

int cmpGreater(Edge a, Edge b)
{
  return a.cost > b.cost;
}

The Repr function returns the representative of the set containing the vertex $v$.

int Repr(int v)
{
  if (v == parent[v]) return v;
  return parent[v] = Repr(parent[v]);
}

The Union function merges sets with elements $x$ and $y$. Implement the heuristic with set sizes.

void Union(int x, int y)
{
  x = Repr(x); y = Repr(y);
  if (x == y) return;
  if (ssize[x] < ssize[y]) swap(x, y);
  parent[y] = x;
  ssize[x] += ssize[y];
}

The main part of the program. Read the number of vertices $n$ in the graph.

scanf("%d", &n);

Initialize the arrays.

parent.resize(n + 1);
ssize.resize(n + 1);
for (i = 0; i <= n; i++)
{
  parent[i] = i;
  ssize[i] = 1;
}

Read the edges of the tree. Store them in the array $e$.

for (i = 0; i < n - 1; i++)
{
  scanf("%d %d %d", &temp.u, &temp.v, &temp.cost);
  e.push_back(temp);
}

Sort the edges in descending order of weights.

sort(e.begin(), e.end(), cmpGreater);

Compute the sum of distances between all pairs of vertices in the variable $res$.

res = 0;

Iterate through the edges. For each edge $(u,v)$ with weight $cost$ call the $Union(u,v)$ function. Add the contribution of all paths with distance $cost$ to $res$.

for (i = 0; i < e.size(); i++)
{
  res += 1LL * e[i].cost * ssize[Repr(e[i].u)] * ssize[Repr(e[i].v)];
  Union(e[i].u, e[i].v);
}

Print the answer.

printf("%lld\n", res);

Python realization

Declare a class $Edge$, describing an edge of the graph.

class Edge:
  def __init__(self, u, v, cost):
    self.u = u
    self.v = v
    self.cost = cost

The cmpGreater function is a comparator that sorts the edges in descending order of weight.

def cmpGreater(a, b):
    return a.cost > b.cost

The Repr function returns the representative of the set containing the vertex $v$.

def Repr(v):
  if v == parent[v]: return v
  parent[v] = Repr(parent[v])
  return parent[v]

The Union function merges sets with elements $x$ and $y$. Implement the heuristic with set sizes.

def Union(x, y):
  x = Repr(x)
  y = Repr(y)
  if x == y: return
  if ssize[x] < ssize[y]:
    x, y = y, x
  parent[y] = x
  ssize[x] += ssize[y]

The main part of the program. Read the number of vertices $n$ in the graph.

n = int(input().strip())

Initialize the lists.

parent = list(range(n + 1))
ssize = [1] * (n + 1)
e = []

Read the edges of the tree. Store them in the list $e$.

for _ in range(n - 1):
  u, v, cost = map(int, input().split())
  e.append(Edge(u, v, cost))

Sort the edges in descending order of weights.

e.sort(key=lambda x: x.cost, reverse=True)

Compute the sum of distances between all pairs of vertices in the variable $res$.

res = 0

Iterate through the edges. For each edge $(u,v)$ with weight $cost$ call the $Union(u,v)$ function. Add the contribution of all paths with distance $cost$ to $res$.

for edge in e:
  res += edge.cost * ssize[Repr(edge.u)] * ssize[Repr(edge.v)]
  Union(edge.u, edge.v)

Print the answer.

print(res)