Disk Sort

You are given $n+1$ rods and $3n$ disks. Initially, each of the first $n$ rods contains exactly $3$ disks. Each of the disks has one of $n$ colors (identified by numbers from $1$ to $n$). Moreover, there are exactly $3$ disks of each of the $n$ colors. The $(n+1)$-th rod is empty.

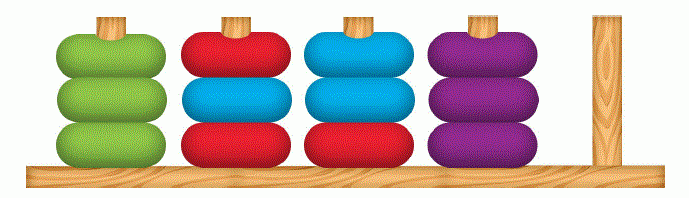
At each step we can select two rods $a$ and $b(a\ne b)$ such that $a$ has at least $1$ disk and $b$ has at most $2$ disks, and move the topmost disk from rod $a$ to the top of rod $b$. Note that no rod is allowed to contain more than $3$ disks at any time.

Your goal is to sort the disks. More specifically, you have to do a number of operations (potentially $0$), so that, at the end, each of the first $n$ rods contains exactly $3$ disks of the same color, and the $(n+1)$-th rod is empty.

Find out a solution to sort the disks in at most $6n$ operations. It can be proven that, under this condition, a solution always exists. If there are multiple solutions, any one is accepted.

Input

The first line contains a positive integer $n(1\le n\le 1000)$. The next $3$ lines contain $n$ positive integers $c_{i,j}(1\le i\le 3,1\le j\le n,1\le c_{i,j}\le n)$ each, the color each of the disks initially placed on the rods. The first of the $3$ lines indicates the upper row, the second line indicates the middle row, and the third line indicates the lower row.

Output

The first line must contain a non-negative integer $k(0\le k\le 6n)$, the number of operations. Each of the following $k$ lines should contain two distinct numbers $a_i,b_i(1\le a_i,b_i\le n+1$, for all $1\le i\le k)$, representing the $i$-th operation (as described in the statement).

Examples