Editorial

Let $s$ be the input string. The substring $s_i...s_j$ is a palindrome if one of the following conditions is satisfied:

• $i\ge j$ (the substring is empty or consists of a single character);

• $s_i=s_j$ and the substring $s_{i+1}...s_{j-1}$ is a palindrome;

Let the function $IsPal(i,j)$ return $1$ if $s_i...s_j$ is a palindrome, and $0$ otherwise. The values of $IsPal(i,j)$ are stored in the cells $pal[i][j]$.

Let the function $f(i,j)$ return the minimum number of cuts required to partition the substring $s_i...s_j$ into palindromes. The values of this function will be stored in the cells of the array $dp[i][j]$. Therefore, the solution to the problem will be $f(0,s.size()-1)$.

Note that $f(i,i)=0$, as a string consisting of a single character is already a palindrome.

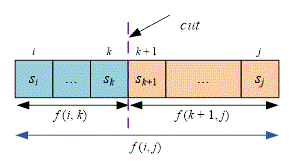
To compute $f(i,j)$, cut the substring $s_i...s_j$ into two parts: $s_i...s_k$ and $s_{k+1}...s_j(i\le k<j)$. Recursively solve the problems on the strings $s_i...s_k$ and $s_{k+1}...s_j$. Look for the value of $k(i\le k<j)$ that minimizes the sum $f(i,k)+f(k+1,j)+1$. The term $+1$ in the sum represents the single cut made between the characters $s_k$ and $s_{k+1}$. Thus, we obtain the following recurrence relation:

Example

For example, for the string "$ababccb$" consisting of $7$ characters, we have:

The sum takes its minimum value at $k=3$:

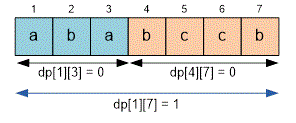
Since the substrings "$aba$" and "$bccb$" are palindromes, $f(1,3)=f(4,7)=0$.

Algorithm implementation

Define the constants, the input string $s$, and the arrays.

#define MAX 1001
#define INF 0x3F3F3F3F
int dp[MAX][MAX], pal[MAX][MAX];
string s;

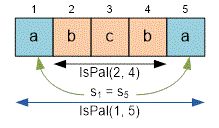
The function $IsPal(i,j)$ checks whether the substring $s_i...s_j$ is a palindrome. The substring $s_i...s_j$ is a palindrome if $s_i=s_j$ and $s_{i+1}...s_{j-1}$ is a palindrome. The values of $IsPal(i,j)$ are stored in the cells of the array $pal[i][j]$.

int IsPal(int i, int j)
{
  if (i >= j) return pal[i][j] = 1;
  if (pal[i][j] != -1) return pal[i][j];
  return pal[i][j] = (s[i] == s[j]) && IsPal(i + 1, j - 1);
}

The function $f(i,j)$ returns the minimum number of cuts required to partition the substring $s_i...s_j$ into palindromes.

int f(int i, int j)
{

If $i=j$, the substring $s_i...s_j$ consists of a single character, and no cuts are needed. If $i>j$, the substring $s_i...s_j$ is considered empty, and no cuts are required.

  if (i >= j) return 0;

If the value $f(i,j)$ is already computed, return the stored value from the $dp[i][j]$.

  if (dp[i][j] != INF) return dp[i][j];

If the substring $s_i...s_j(i<j)$ is a palindrome, there is no need to make any cuts. In this case, the minimum number of cuts is $0$.

  if (IsPal(i, j)) return dp[i][j] = 0;

Cut the substring $s_i...s_j$ into two parts: $s_i...s_k(i\le k)$ and $s_{k+1}...s_j(k+1\le j)$. Then, recursively solve the problems for both parts: $s_i...s_k$ and $s_{k+1}...s_j$. Find the value of $k(i\le k<j)$ for which the sum $f(i,k)+f(k+1,j)+1$ is minimized.

  for (int k = i; k < j; k++)
    dp[i][j] = min(dp[i][j], f(i, k) + f(k + 1, j) + 1);

Return the answer $dp[i][j]=f(i,j)$.

  return dp[i][j];
}

The main part of the program. Read the input string.

cin >> s;

Initialize the arrays.

memset(dp, 0x3F, sizeof(dp));
memset(pal, -1, sizeof(pal));

Compute and print the answer.

res = f(0, s.size() - 1);
cout << res << endl;