Editorial

Consider the size of a rectangle $a \times b$ drawn on the grid. Let's examine how many ways we can choose the value of $a$ . The grid contains $n$ rows of squares, and therefore there are $n + 1$ horizontal lines in the grid. Let's number them from $1$ to $n + 1$ . We choose two lines $i$ and $j (i < j)$ . Drawing a segment between them forms the vertical side a of the rectangle. The number of ways to choose two numbers $i$ and $j (i < j)$ from the set ${1, 2, ..., n + 1}$ is equal to $C_{n + 1}^{2}$ . For example, for $n = 2$ there are $3$ options to choose the vertical side of the rectangle:

Similarly, the grid has $m + 1$ vertical lines. The number of ways to select the horizontal side of a rectangle is $C_{m + 1}^{2}$ .

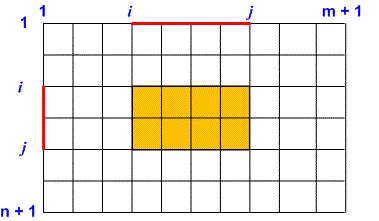
Therefore the number of different rectangles on the grid is equal to

C_{n + 1}^{2} \cdot C_{m + 1}^{2} = \frac{( n + 1 ) \cdot n}{2} \cdot \frac{( m + 1 ) \cdot m}{2}

Example

For a $2 \times 3$ rectangle there are:

$6$ rectangles of size $1 \cdot 1$ ;

$4$ rectangles of size $1 \cdot 2$ ;

$2$ horizontal rectangles $1 \cdot 3$ ;
$3$ vertical rectangles $2 \cdot 1$ ;

$2$ rectangles $2 \cdot 2$ ;
$1$ rectangle $2 \cdot 3$ ;

The total result is $C_{3}^{2} \cdot C_{4}^{2} = 3 \cdot 6 = 18$ rectangles.

Algorithm realization

Since $n, m \leq 1 0^{5}$ , the number of rectangles can be as large as $C_{n + 1}^{2} \cdot C_{m + 1}^{2} \leq (1 0^{5})^{2} \cdot (1 0^{5})^{2} = 1 0^{20}$ . This result is beyond the bounds of a $64$ -bit integer. Therefore, let's implement the solution in Python.

n, m = map(int,input().split())
a = (n + 1) * n // 2
b = (m + 1) * m // 2
res = a * b
print(res)