Editorial

The task is to decompose the tree into connected components with an even number of vertices, while maximizing the number of such components.

We'll perform a depth-first search starting from vertex $1$, which is the root of the tree. For each vertex $v$, we'll determine the number of vertices in the subtree rooted at $v$. If this number is even, we'll remove the edge connecting $v$ to its parent in the depth-first search.

For the root (vertex $1$), the size of the entire tree is even. However, there is no edge connecting vertex $1$ to its parent, so we must subtract $1$ from the result obtained using the above algorithm.

Example

Consider the tree shown in the example. Next to each vertex is the size of the subtree when that vertex is considered as the root. Vertices $1,3$, and $6$ have subtrees with an even number of vertices. Since vertex $1$ is the root and does not have an edge leading to a parent, we remove two edges: $(1,3)$ and $(1,6)$.

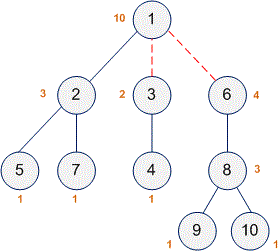
The tree has been decomposed into $3$ connected components, each containing an even number of vertices.

Algorithm realization

Declare the arrays.

#define MAX 101
int g[MAX][MAX], used[MAX];

The dfs function performs a depth-first search starting from vertex $v$ and returns the number of vertices in the subtree rooted at $v$.

int dfs(int v)
{
  used[v] = 1;

In the variable $s$, compute the number of vertices in the subtree rooted at $v$.

  int s = 1;

Iterate over the children $i$ of vertex $v$. Add the values of $dfs(i)$ to $s$.

  for (int i = 1; i <= n; i++)
    if (g[v][i] && !used[i]) s += dfs(i);

If the size of the subtree $s$ is even, remove the edge between $v$ and its parent.

  if (s % 2 == 0) res++;

Return the number of vertices in the subtree rooted at $v$.

  return s;
}

The main part of the program. Read the input data and build the graph.

scanf("%d %d", &n, &m);
for (i = 0; i < m; i++)
{
  scanf("%d %d", &a, &b);
  g[a][b] = g[b][a] = 1;
}

Start a depth-first search from vertex $1$. In the variable $res$, count the number of removed edges.

res = 0;
dfs(1);

Since there is no edge from $1$ to its parent, print $res-1$.

printf("%d\n", res - 1);

Python realization

The dfs function performs a depth-first search starting from vertex $v$ and returns the number of vertices in the subtree rooted at $v$.

def dfs(v):
  used[v] = 1

In the variable $s$, compute the number of vertices in the subtree rooted at $v$.

  s = 1

Iterate over the children $i$ of vertex $v$. Add the values of $dfs(i)$ to $s$.

  for i in range(1, n + 1):
    if g[v][i] and not used[i]:
      s += dfs(i)

If the size of the subtree $s$ is even, remove the edge between $v$ and its parent.

  if s % 2 == 0:
    global res
    res += 1

Return the number of vertices in the subtree rooted at $v$.

  return s

The main part of the program. Read the input data and build the graph.

n, m = map(int, input().split())
g = [[0] * (n + 1) for _ in range(n + 1)]
used = [0] * (n + 1)

for _ in range(m):
  a, b = map(int, input().split())
  g[a][b] = g[b][a] = 1

Start a depth-first search from vertex $1$. In the variable $res$, count the number of removed edges.

res = 0
dfs(1)

Since there is no edge from $1$ to its parent, print $res-1$.

print(res - 1)