Tree Permutations

Once upon a time, Mr. Cool created a tree (an undirected graph without cycles) of n vertices, by assigning to each vertex i > 1 two numbers: p[i] < i - the direct ancestor of vertex i and w[i] - the weight of the edge between vertex i and p[i]. Vertex 1 is the root, so it does not have any ancestors.

You wanted to know what tree did Mr. Cool build, but Mr. Cool refused to tell this, but he gave you a tip:

He wrote all these numbers in one line. That’s how he got array b of length 2 * n - 2.

b = [p[2], w[2], p[3], w[3], ..., p[n-1], w[n-1], p[n], w[n]]

Then he randomly shuffled it. That’s how he got array a, and Mr. Cool presented you with it. Since it is impossible to restore the tree knowing only values of array a, you decided to solve a different problem.

Let’s call a tree k-long, if there are exactly k edges on the path between vertex 1 and n.

Let’s call a tree k-perfect, if it is k-long and the sum of the weights of the edges on the path between vertex 1 and vertex n is maximal among all possible k-long trees that Mr. Cool could build.

Your task is to print the sum of the weights of the edges on the path between vertex 1 and vertex n for all possible k-perfect trees or print -1 if a certain k-long tree could not be built by Mr. Cool.

Input

The first line contains one integer n (2 ≤ n ≤ 10^5) - the number of the vertices in the tree.

The second line contains 2 * n - 2 integers a[1], a[2], ..., a[2n-2] (1 ≤ a[i] ≤ n - 1) - the elements of array a.

Output

In one line, print n - 1 integers w[1], w[2], w[3], ..., w[n-1], where w[k] is the sum of the weights of the edges on the path between vertex 1 and vertex n in a k-perfect tree. If there is no i-long tree, then w[i] should be equal to -1.

Examples

Note

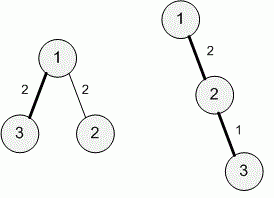
In the first example, the 1-perfect tree is defined by array [1, 2, 1, 2] (i.e. p[2] = 1, w[2] = 2, p[3] = 1, w[3] = 2).

The 2-perfect tree is defined by array [1, 2, 2, 1] (i.e p[2] = 1, w[2] = 2, p[3] = 2, w[3] = 1). Here are illustrations of the 1-perfect tree and the 2-perfect tree respectively (path from vertex 1 to vertex n is drawn with bold lines):

In the second example, there are no k-perfect trees, that can be obtained by permuting array a.

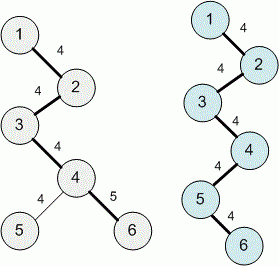
In the third example, only 4-perfect tree and 5-perfect tree can be obtained. These are defined by arrays [1, 4, 2, 4, 3, 4, 4, 4, 4, 5] and [1, 4, 2, 4, 3, 4, 4, 4, 5, 4] respectively. Here are illustrations of them: