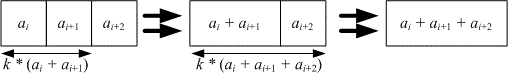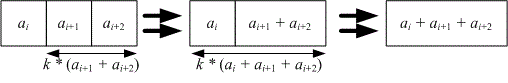Editorial

Let $f (i, j)$ represent the minimum cost to reduce the subarray $[a_{i}, ..., a_{j}]$ to a single element. This value will be stored in the cell $d p [i] [j]$ .

Obviously, $f (i, i) = 0$ .

From the problem statement, it follows that

f (i, i + 1) = k \cdot (a_{i} + a_{i + 1})

Now, let’s compute $f (i, i + 2)$ . Reducing three numbers into one can be done in two ways:

Merge $a_{i}$ and $a_{i + 1}$ with a cost of $k \cdot (a_{i} + a_{i + 1})$ , then merge $a_{i} + a_{i + 1}$ and $a_{i + 2}$ at a cost of $k \cdot (a_{i} + a_{i + 1} + a_{i + 2})$ .
Merge $a_{i + 1}$ and $a_{i + 2}$ with a cost of $k \cdot (a_{i + 1} + a_{i + 2})$ , then merge $a + i$ and $a_{i + 1} + a_{i + 2}$ at a cost of $k \cdot (a_{i} + a_{i + 1} + a_{i + 2})$ .

Thus

f (i, i + 2) = min (k \cdot (a_{i} + a_{i + 1}) + k \cdot (a_{i} + a_{i + 1} + a_{i + 2}), k \cdot (a_{i + 1} + a_{i + 2}) + k \cdot (a_{i} + a_{i + 1} + a_{i + 2}))

Now, let’s consider calculating the value of $f (i, j)$ . To reduce the subarray $[a_{i}, ..., a_{j}]$ to a single element equal to $a_{i} + ... + a_{j}$ , we need to choose some value $p (i \leq p < j)$ . Then, recursively solve the problem for the subarrays $[a_{i}, ..., a_{p}]$ and $[a_{p + 1}, ..., a_{j}]$ , and finally merge the elements $a_{i} + ... + a_{p}$ and $a_{p + 1} + ... + a_{j}$ . The value of $p$ should be chosen in such a way that the total transformation cost is minimized:

f (i, j) = i \leq p < j min (f (i, p) + f (p + 1, j)) + k \cdot (a_{i} + ... + a_{j})

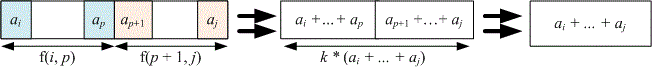
For efficient computation of sums $a_{i} + ... + a_{j}$ use a prefix sum array $p re f$ , where

p re f [i] = a_{1} + ... + a_{i},

so that $a_{i} + ... + a_{j} = p re f [j] - p re f [i - 1]$ .

Algorithm implementation

Let’s declare constants and arrays.

#define MAX 101
#define INF 0x3F3F3F3F
int dp[MAX][MAX], a[MAX], pref[MAX];

The function $f (i, j)$ returns the minimum cost to transform the subarray $[a_{i}, ..., a_{j}]$ into a single element.

int f(int i, int j)
{
  if (dp[i][j] == INF)
    for (int p = i; p < j; p++)
      dp[i][j] = min(dp[i][j], f(i, p) + f(p + 1, j) + (pref[j] - pref[i - 1]) * k);
    return dp[i][j];
}

The main part of the program. Read the input data.

scanf("%d %d", &n, &k);
memset(dp, 0x3F, sizeof(dp));
for (i = 1; i <= n; i++)
{
  scanf("%d", &a[i]);
  dp[i][i] = 0;

Compute the array of prefix sums.

  pref[i] = pref[i - 1] + a[i];
}

Compute and print the answer.

printf("%d\n", f(1, n));

Python implementation

Let’s declare the constant for infinity.

INF = float('inf')

The function $f (i, j)$ returns the minimum cost to transform the subarray $[a_{i}, ..., a_{j}]$ into a single element.

def f(i, j):
  if dp[i][j] == INF:
    for p in range(i, j):
      dp[i][j] = min(dp[i][j], f(i, p) + f(p + 1, j) + (pref[j] - pref[i - 1]) * k)
  return dp[i][j]

The main part of the program. Read the input data.

n, k = map(int, input().split())
a = [0] + list(map(int, input().split()))

Compute the array of prefix sums.

pref = [0] * (n + 1)
for i in range(1, n + 1):
  pref[i] = pref[i - 1] + a[i]

Initialize the $d p$ array.

dp = [[INF] * (n + 1) for _ in range(n + 1)]
for i in range(1, n + 1):
  dp[i][i] = 0

Compute and print the answer.

print(f(1, n))