Editorial

Let $cos t [i]$ be the cost of gasoline in the $i$ -th city. For each pair of cities $i$ and $j$ , add a directed edge from $i$ to $j$ with weight $cos t [i]$ , as well as a directed edge from $j$ to $i$ with weight $cos t [j]$ .

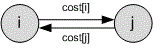
To solve the problem, find the minimum cost path from city $1$ to city $n$ .

Example

Let’s construct the graph given in the first example.

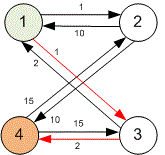
The minimum cost route from vertex $1$ to vertex $4$ is: $1 \to 3 \to 4$ . Its cost is $1 + 2 = 3$ .

Algorithm realization

Store the graph in an adjacency matrix $g$ . The current shortest distances from the starting vertex $1$ to the other vertices are stored in an array $d$ . The array $cos t$ holds the gasoline cost in each city.

#define MAX 110
#define INF 0x3F3F3F3F
int g[MAX][MAX], used[MAX], d[MAX], cost[MAX];

Read the number of cities $n$ and the gasoline cost in each of them.

scanf("%d",&n);
for(i = 1; i <= n; i++)
  scanf("%d",&cost[i]);

Construct a graph representing the costs of traveling between cities.

memset(g,0x3F,sizeof(g));
memset(used,0,sizeof(used));
scanf("%d",&m);
for(i = 1; i <= m; i++)
{
  scanf("%d %d",&a,&b);
  g[a][b] = cost[a];
  g[b][a] = cost[b];
}

Initialize the shortest distances from the first vertex to the other vertices.

memset(d,0x3F,sizeof(d));
d[1] = 0;

Start the loop of Dijkstra's algorithm. In each iteration find the vertex $w$ with the minimum distance $min d$ from the starting vertex.

for(i = 1; i < n; i++)
{
  mind = INF; w = -1;
  for(j = 1; j <= n; j++)
    if (!used[j] && d[j] < mind) {mind = d[j]; w = j;}

If it turns out that $w = - 1$ , then the desired path does not exist, and we exit the loop.

  if (w < 0) break;

Relax all edges originating from vertex $w$ .

  for (j = 1; j <= n; j++)
    if (!used[j]) d[j] = min(d[j], d[w] + g[w][j]);

The shortest distance to vertex $w$ is computed.

  used[w] = 1;
}

Print the answer based on the value of $d i s t [n]$ . If it is infinity, then there is no path to vertex $n$ . Otherwise, print the shortest distance found.

if (d[n] == INF) printf("-1\n");
else printf("%d\n",d[n]);

Java realization

import java.util.*;

public class Main
{
  static final int INFINITY = 2000000000;
  static int g[][], used[], dist[], cost[];	

  static void Relax(int i, int j)
  {
    if (dist[i] + g[i][j] < dist[j])
      dist[j] = dist[i] + g[i][j];
  }
	
  public static void main(String[] args) 
  {
    Scanner con = new Scanner(System.in);
    int n = con.nextInt();
    g = new int[n+1][n+1]; 
    for (int[] row: g) Arrays.fill(row, INFINITY);

    cost = new int[n+1];
    for (int i = 1; i <= n; i++)
      cost[i] = con.nextInt();
    
    used = new int[n+1]; Arrays.fill(used, 0);
    dist = new int[n+1]; Arrays.fill(dist, INFINITY);
    dist[1] = 0;
	
    int m = con.nextInt();
    for (int i = 1; i <= m; i++)
    {
      int a = con.nextInt();
      int b = con.nextInt();
      g[a][b] = cost[a];
      g[b][a] = cost[b];

    }
    
    for (int i = 1; i < n; i++)
    {
      // find vertex w with minimum d[w] among not used vertices
      int min = INFINITY, v = -1;
      for (int j = 1; j <= n; j++)
        if (used[j] == 0 && dist[j] < min) { min = dist[j]; v = j; }

      // no more vertices to add
      if (v < 0) break;

      // relax all edges outgoing from v
      // process edge v -> j
      for (int j = 1; j <= n; j++)
        if (used[j] == 0 && g[v][j] != -1) Relax(v, j);

      // shortest distance to v is found
      used[v] = 1;
    }

    if (dist[n] == INFINITY) System.out.println(-1);
    else System.out.println(dist[n]);

    con.close();
  }
}