Editorial

The problem provides an undirected connected graph. It is necessary to check whether it contains a cycle (which can be turned into a Formula-0 track).

An undirected graph contains a cycle if there is a back edge, i.e., an edge leading to a vertex that is already visited.

Example

The graphs given in the example are as follows:

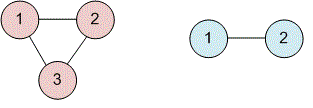
The first graph contains a cycle, while the second does not.

Algorithm realization

The graph is stored in the adjacency matrix $g$. The array used is used to mark the visited vertices.

#define MAX 1010
int g[MAX][MAX], used[MAX];

The dfs function implements depth-first search from vertex $v$. It is necessary to exclude the case when we move from $v$ to its ancestor: the ancestor is already visited, but there is no cycle. To handle this, we will introduce a second parameter $p$ in the dfs function, representing the ancestor of vertex $v$.

void dfs(int v, int p = -1)
{

Mark vertex $v$ as visited.

  used[v] = 1;

Iterate over the vertices $i$ that can be reached from $v$.

  for (int i = 1; i <= n; i++)
  {

Consider all edges except for the one that leads to the ancestor $p$.

    if (i == p) continue;

If there is an edge from $v$ to $i$, and $i$ is already visited ($used[i]=1$), then the graph contains a cycle. Set $flag=1$.

    if (g[v][i] == 1)
    {
      if (used[i] == 1) flag = 1;

Otherwise, continue the depth-first search from vertex $i$.

      else dfs(i, v);
    }
  }
}

The main part of the program. Read the input data.

scanf("%d %d",&n,&m);
memset(g,0,sizeof(g));
memset(used,0,sizeof(used));

Read the input undirected graph. The graph is stored in an adjacency matrix, so repeated roads will be counted only once.

for (i = 0; i < m; i++)
{
  scanf("%d %d",&u,&v);  
  g[u][v] = g[v][u] = 1;
}

Set $flag=0$, which indicates the absence of a cycle in the graph. If a cycle is found, the value of $flag$ will change to $1$.

flag = 0;

Initiate depth-first search from vertex $1$ (according to the problem statement, the graph is connected).

dfs(1);

Based on the value of $flag$, print the result.

if (flag) printf("YES\n");
else printf("NO\n");

Java realization

import java.util.*;

public class Main
{
  static int g[][], used[];
  static int n, m, flag;

  static void dfs(int v, int prev)
  {
    used[v] = 1;
    for(int i = 1; i <= n; i++)
      if ((i != prev) && g[v][i] == 1)
        if (used[i] == 1) flag = 1; else dfs(i,v);
  }
  
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    n = con.nextInt();
    m = con.nextInt();    
    g = new int[n+1][n+1];
    used = new int[n+1];

    for(int i = 0; i < m; i++)
    {
      int u = con.nextInt();
      int v = con.nextInt();
      g[u][v] = g[v][u] = 1; 
    }
    
    flag == 0;
    dfs(1,-1);

    if (flag == 1) System.out.println("YES");
    else System.out.println("NO");
  }
}