Algorithm Analysis

For ease of further calculations, we flip the board from bottom to top. We will number the cells vertically and horizontally from 1. Then, the mouse's route will go from the top left corner – the cell with coordinates $(1,1)$, to the bottom right – the cell with coordinates $(m,n)$. And the movement down the board will be coded with the letter F.

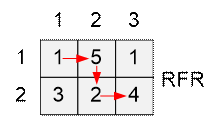
Let the tile with coordinates $(i,j)$ have $a[i][j]$ grains. Let $res[i][j]$ contain the maximum number of grains that can be collected when moving from the top left corner to the cell $(i,j)$. Since the tile $(i,j)$ can be reached either from the tile $(i–1,j)$, or from $(i,j–1)$, then

$res[i][j]=max(res[i–1][j],res[i][j–1])+a[i][j]$

It is also possible to do without the array res, performing calculations in the array a itself. We will pass the floor tiles (array cells) from top to bottom and from left to right, setting

$a[i][j]=max(a[i–1][j],a[i][j–1])+a[i][j]$

Initially, all cells of the zeroth row and the zeroth column of the array a are initialized to -1. However, for correct recalculation of the value a[1][1], one of the cells should be zeroed: a[0][1] or a[1][0]. In this case, the new value of the cell a[1][1] will be equal to max(a[0][1], a[1][0]) + a[1][1] = 0 + a[1][1] = a[1][1]. Subsequently, all values of a[i][j] will be recalculated correctly.

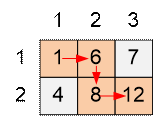
After the calculations, $a[i][j]$ will already contain the maximum number of grains that can be collected upon reaching the tile $(i,j)$. The state of the array a at the end of the calculations:

Algorithm Implementation

The input information about the grains will be stored in the array a. That is, on the tile with coordinates $(i,j)$, there are $a[i][j]$ grains. The mouse's movement route will be stored in the array pos, which has a length of $m+n–1$ ($m$ and $n$ are the floor dimensions).

#define MAX 102
int a[MAX][MAX];
char pos[2MAX];

We read the input data. Since there can also be 0 grains on the tiles, we initialize the array cells with the numbers -1. We flip the board from bottom to top.

scanf("%d %d",&m,&n);
memset(a,-1,sizeof(a));
for(i = 1; i <= m; i++)
    for(j = 1; j <= n; j++)
        scanf("%d",&a[m-i+1][j]);

We recalculate the cells of the array a so that $a[i][j]$ contains the maximum number of grains that can be collected upon reaching the tile $(i,j)$.

a[0][1] = 0;
for(i = 1; i <= m; i++)
    for(j = 1; j <= n; j++)
        a[i][j] = max(a[i-1][j],a[i][j-1]) + a[i][j];

Starting from the tile $(i,j)=(m,n)$, we move to the tile $(1,1)$ recording the mouse's movement route in the array pos. From the tile $(i,j)$, it is necessary to move to $(i–1,j)$ or $(i,j–1)$, depending on which of the values $a[i–1][j]$ or $a[i][j–1]$ is greater.

i = m; j = n; ptr = 0;
while(i + j > 2)
{
    if (a[i-1][j] > a[i][j-1])
    {
        pos[ptr] = 'F';
        i--;
    }
    else
    {
        pos[ptr] = 'R';
        j--;
    }
    ptr++;
}

We print the mouse's movement route.

while(ptr--) printf("%c",pos[ptr]);
printf("\n");