Editorial

The greatest common divisor (gcd) of two integers is defined as the largest non-negative integer that divides both of these integers. For example, $GCD(8,12)=4$.

It is known that $GCD(0,x)=|x|$ (the absolute value of $x$), because $|x|$ is the largest non-negative integer that divides $0$ and $x$. For example, $GCD(-6,0)=6,GCD(0,5)=5$.

To find the gcd of two numbers, you can use an iterative algorithm: subtract the smaller number from the larger one. When one of the numbers becomes $0$, the other one becomes the gcd. For example, $GCD(10,24)=GCD(10,14)=GCD(10,4)=GCD(6,4)=GCD(2,4)=GCD(2,2)=GCD(2,0)=2$.

If instead of the "subtraction" operation, you use the "modulo" operation, the calculations will proceed significantly faster.

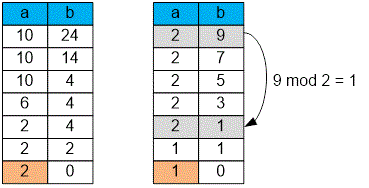
For example, to find $GCD(1,10^9)$ uning subtraction, you would need to perform $10^9$ operations. Using the modulo operation, only one action is required.

The GCD of two numbers can be computed using the formula:

or the same as

The iterative implementation is based on the idea presented in the final recurrence relation:

while (b > 0) :
    compute a = a % b;
    swap the contents of variables a and b;

Algorithm implementation

The gcd function computes the GCD of two numbers.

int gcd(int a, int b)
{
  if (a == 0) return b;
  if (b == 0) return a;
  if (a >= b) return gcd(a % b, b);
  return gcd(a, b % a);
}

The main part of the program. Read the input data.

scanf("%d %d",&a,&b);

Compute and print the GCD of two numbers.

d = gcd(a,b);
printf("%d\n",d);

Algorithm implementation — simplified recursion

The gcd function computes the GCD of two numbers.

int gcd(int a, int b)
{
  return (!b) ? a : gcd(b,a % b);
}

The main part of the program. Read the input data.

scanf("%d %d",&a,&b);

Compute and print the GCD of two numbers.

d = gcd(a,b);
printf("%d\n",d);

Algorithm implementation — iterative

The gcd function computes the GCD of two numbers.

int gcd(int a, int b)
{
  while (b > 0)
  {
    a = a % b;
    int temp = a; a = b; b = temp;
  }
  return a;
}

The main part of the program. Read the input data.

scanf("%d %d",&a,&b);

Compute and print the GCD of two numbers.

d = gcd(a,b);
printf("%d\n",d);

Java implementation

import java.util.*;

public class Main
{
  static int gcd(int a, int b)
  {
    if (a == 0) return b;
    if (b == 0) return a;
    if (a >= b) return gcd(a % b, b);
    return gcd(a, b % a);
  }
    
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    int a = con.nextInt();
    int b = con.nextInt();
    
    int res = gcd(a, b);
    System.out.println(res);
    con.close();
  }
}

Python implementation — recursion

The gcd function computes the GCD of two numbers.

def gcd(a, b):
  if a == 0: return b
  if b == 0: return a
  if a > b: return gcd(a % b, b)
  return gcd(a, b % a)

The main part of the program. Read the input data.

a, b = map(int, input().split())

Compute and print the GCD of two numbers.

print(gcd(a, b))

Python implementation — gcd

To compute the greatest common divisor (GCD) of two numbers, let's use the gcd function built into the Python language.

import math

Read the input data.

a, b = map(int, input().split())

Compute and print the GCD of two numbers.

print(math.gcd(a, b))