Vasyas triangles
Vasya built an equilateral triangle with sides equal to 1, called him and arranged A_1B_1C_1 one side of the axis OX so that its midpoint located exactly at the origin and the vertex A_1 was placed on the positive half-OY. Each subsequent Vasin equilateral triangle has a length of exactly 2 more to the right and placed last, so that one of the peaks coincides with the OX axis at right top of the previous triangle and vertex A_n available in the upper half.
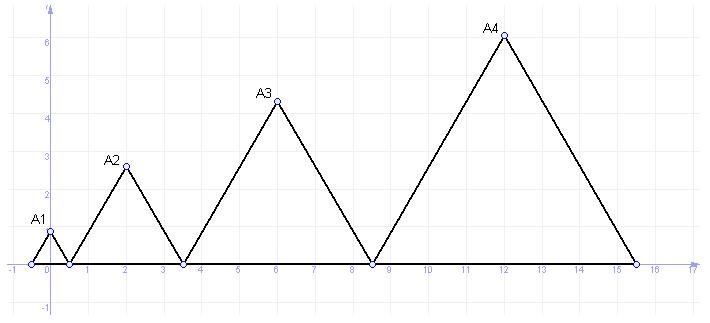
Vasya now interested in the question: what are the coordinates of a vertex A_n n-th triangle? Help him.
Input
The single line of input file specified number of triangle n (1 ≤ n ≤ 10^4).
Output
In a single line of output file output with three characters after the decimal point vertex coordinates A_n X_n and Y_n are interested Vasya triangle, separated by one space.