Basecamp
    Home
    Problems
    Contests
    Courses
    Ranking
    Posts
2403
Strong connectivity
Sign in
StatementDiscussionEditorial

Editorial

Find the number of strongly connected components in the directed graph.

Example

Graphs, given in samples, have the form:

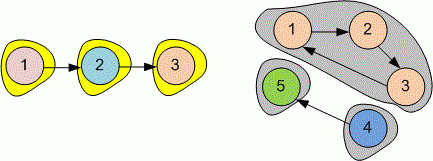
Each of these graphs has 3 strongly connected components.

Algorithm realization

The input graph is stored in the adjacency list g. The inverse graph is stored in the adjacency list gr.

vector<vector<int> > g, gr;
vector<int> used, top;

The function dfs1 implements depth-first search on the input graph. It adds vertices to the array top in the order in which the depth-first search finishes processing them.

void dfs1(int v)
{
  used[v] = 1;
  for (int to : g[v])
    if (!used[to]) dfs1(to);
  top.push_back(v);
}
C++
7 lines
114 bytes

The function dfs2 implements depth-first search on the reversed graph. All vertices traversed during a recursive call of dfs2 belong to one strongly connected component.

void dfs2(int v)
{
  used[v] = 1;
  for (int to : gr[v])
    if (!used[to]) dfs2(to);
}

The main part of the program. Read the input data. Construct the reversed graph.

scanf("%d %d", &n, &m);
g.resize(n + 1);
gr.resize(n + 1);
for(i = 1; i <= m; i++)
{
  scanf("%d %d",&a,&b);
  g[a].push_back(b);
  gr[b].push_back(a);
}
C++
9 lines
163 bytes

Run a depth-first search on the input graph. The order in which the vertices finish processing is stored in the top array.

used.resize(n+1);
for(i = 1; i <= n; i++)
  if (!used[i]) dfs1(i);

Run a depth-first search on the reversed graph. The vertices of the reversed graph should be processed in the order given by traversing the array top from right to left (from end to start). For convenience in further processing, let’s reverse the array top.

used.clear();
used.resize(n + 1);
reverse(top.begin(), top.end());

Use the variable c to count the number of strongly connected components.

c = 0;

Now move through the array top from left to right and call dfs2 from each unvisited vertex.

for (int v : top)
  if (!used[v])
  {
    dfs2(v);
    c++;
  }

Print the number of strongly connected components in the graph.

printf("%d\n",c);

Java realization

import java.util.*;

public class Main
{
  static ArrayList<Integer>[] g, gr;	
  static boolean used[];
  static Vector<Integer> top = new Vector<Integer>();

  static void dfs1(int v)
  {
    used[v] = true;
    for(int i = 0; i < g[v].size(); i++)
    {
      int to = g[v].get(i);
      if (!used[to]) dfs1(to);
    }
    top.add(v);
  }

  static void dfs2(int v)
  {
    used[v] = true;
    for(int i = 0; i < gr[v].size(); i++)
    {
      int to = gr[v].get(i);
      if (!used[to]) dfs2(to);
    }
  }
  
  @SuppressWarnings("unchecked")  
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    int n = con.nextInt();
    int m = con.nextInt();
    
    g = new ArrayList[n+1];
    for(int i = 0; i <= n; i++)
      g[i] = new ArrayList<Integer>();
    gr = new ArrayList[n+1];
    for(int i = 0; i <= n; i++)
      gr[i] = new ArrayList<Integer>();
    
    for (int i = 0; i < m; i++)
    {
      int a = con.nextInt();
      int b = con.nextInt();
      g[a].add(b);
      gr[b].add(a);
    }

    used = new boolean[n+1];
    for(int i = 1; i <= n; i++)
      if (!used[i]) dfs1(i);
    
    used = new boolean[n+1];
    int c = 0;
    for(int i = 1; i <= n; i++)
    {
      int v = top.get(n-i);
      if (!used[v])
      {
        dfs2(v);
        c++;
      }
    }
    
    System.out.println(c);
    con.close();
  }
}
Java
71 lines
1447 bytes

Python realization

The function dfs1 implements depth-first search on the input graph. It adds vertices to the array top in the order in which the depth-first search finishes processing them.

def dfs1(v):
  global g, used, top
  used[v] = True
  for to in g[v]:
    if not used[to]: dfs1(to)
  top.append(v)

The function dfs2 implements depth-first search on the reversed graph. All vertices traversed during a recursive call of dfs2 belong to one strongly connected component.

def dfs2(v):
  global gr, used
  used[v] = True
  for to in gr[v]:
    if not used[to]: dfs2(to)

The main part of the program. Read the input data. Construct the reversed graph.

n, m = map(int, input().split())
g = [[] for _ in range(n + 1)]
gr = [[] for _ in range(n + 1)]

for _ in range(m):
  a, b = map(int, input().split())
  g[a].append(b)
  gr[b].append(a)
Python
8 lines
194 bytes

Run a depth-first search on the input graph. The order in which the vertices finish processing is stored in the top array.

used = [False] * (n + 1)
top = []

for i in range(1, n + 1):
  if not used[i]: dfs1(i)

Run a depth-first search on the reversed graph. The vertices of the reversed graph should be processed in the order given by traversing the array top from right to left (from end to start). For convenience in further processing, let’s reverse the array top.

used = [False] * (n + 1)
top.reverse()

Use the variable c to count the number of strongly connected components.

c = 0

Now move through the array top from left to right and call dfs2 from each unvisited vertex.

for v in top:
  if not used[v]:
    dfs2(v)
    c += 1

Print the number of strongly connected components in the graph.

print(c)
Loading...
Loading...