Editorial

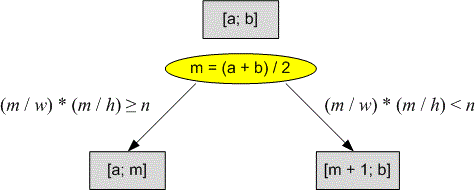
Let $x$ be the required length of the side of the square board. Search for $x$ using binary search. Obviously, $0<x\le max(w,h)\cdot n$. Start the search in the interval $[a;b]=[0;max(w,h)\cdot n]$.

Let $m=(a+b)/2$ be the current length of the side of the board. Since the diploma has a size of $w\cdot h$, the board can accommodate a maximum of $(m/w)\cdot (m/h)$ diplomas. If this number is less than $n$, then the board size is too small, and we set $a=m+1$. Otherwise, we move the right search boundary: $b=m$.

Let the size of the diploma is $w\times h=2\times 3$.

• On a $8\times 8$ board, you can place a maximum of $(8/2)\cdot (8/3)=4\cdot 2=8$ diplomas;

• On a $9\times 9$ board, you can place a maximum of $(9/2)\cdot (9/3)=4\cdot 3=12$ diplomas;

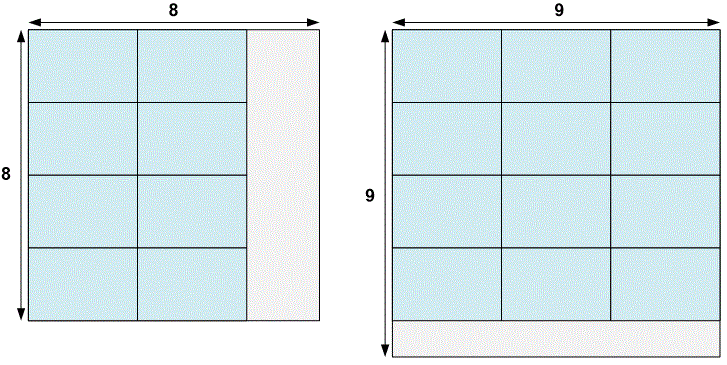
The minimum size of the board’s side, where you can place $10$ diplomas, is $9$.

Algorithm realization

Read the input data.

scanf("%lld %lld %lld", &w, &h, &n);

Set the boundaries of the binary search to $[a;b]=[0;max(w,h)\cdot n]$.

a = 0;
b = max(w, h) * n;

Start the binary search.

while (a < b)
{
  m = (a + b) / 2;

The maximum number of diplomas of size $w\cdot h$ that can be arranged on the board with side length $m$ is $dip=(m/w)\cdot (m/h)$.

  dip = (m / w) * (m / h);
  if (dip < n) a = m + 1;
  else b = m;
}

Print the answer.

printf("%lld\n", b);

Python realization

Read the input data.

w, h, n = map(int, input().split())

Set the boundaries of the binary search to $[a;b]=[0;max(w,h)\cdot n]$.

a = 0
b = max(w, h) * n

Start the binary search.

while a < b:
  m = (a + b) // 2

The maximum number of diplomas of size $w\cdot h$ that can be arranged on the board with side length $m$ is $dip=(m/w)\cdot (m/h)$.

  dip = (m // w) * (m // h)
  if dip < n:
    a = m + 1
  else:
    b = m

Print the answer.

print(b)