Editorial

The task of this problem is to find the longest common subsequence (LCS) of two strings and print it.

Construct an array $dp$, where $dp[i][j]$ represents the length of the LCS of the substrings $x_{[1\dots i]}$ and $y_{[1\dots j]}$. The value $dp[n][m]$ will correspond to the length of the LCS of the original strings ($|x|=n,|y|=m$).

After computing the $dp$ array, reconstruct the LCS by performing a reverse traversal of the matrix $dp$ from cell $(n,m)$ to $(0,0)$. At each position $(i,j)$, we follow the next steps:

• If the characters $x_i$ and $y_j$ match, this character is part of the LCS. Add it to the resulting string $res$, and move diagonally to cell $(i-1,j-1)$, continuing to build the LCS for $x_{[1\dots i-1]}$ and $y_{[1\dots j-1]}$.

• If the characters $x_i$ and $y_j$ do not match, move to the cell with the larger value, either $(i,j-1)$ or $(i-1,j)$. If $dp[i-1][j]$ and $dp[i][j-1]$ are equal, you may choose either cell.

The resulting string $res$ will contain the longest common subsequence of $x$ and $y$.

Example

Let us examine the process of finding the longest common subsequence (LCS) for two strings provided in the example.

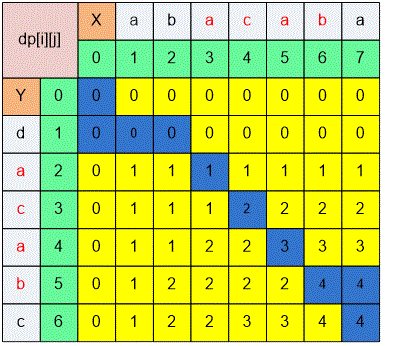
The search for the LCS starts at position $(i,j)=(6,7)$.

$y[6]\ne x[7]$: move to any adjacent cell with the maximum value, for example, $(5,7)$.

$y[5]\ne x[7]$: move to $(5,6)$.

$y[5]=x[6]=$ '$b$': make a diagonal move and include the character '$b$' in the LCS.

Algorithm implementation

Declare the input strings $x$ and $y$. To find their LCS, we'll use the $dp$ array.

#define MAX 1001
int dp[MAX][MAX];
string x, y, res;

Read the input strings. Add a space in front of each of them so that indexing starts from $1$.

cin >> x; n = x.length(); x = " " + x;
cin >> y; m = y.length(); y = " " + y;

Compute the LCS.

for (i = 1; i <= n; i++)
for (j = 1; j <= m; j++)
  if (x[i] == y[j])
    dp[i][j] = dp[i - 1][j - 1] + 1;
  else
    dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

Build the LCS in the string $res$.

i = n; j = m;
while (i >= 1 && j >= 1)
  if (x[i] == y[j])
  {
    res = res + x[i];
    i--; j--;
  }
  else
  {
    if (dp[i - 1][j] > dp[i][j - 1])
      i--;
    else
      j--;
  }

Invert and print the resulting string.

reverse(res.begin(), res.end());
cout << res << endl;