Editorial

Let's fix $j$ (for example $j=12$) and find the number of $i$ such that $i=GCD(i,12)$.

The values of $i$ that satisfy this equation are $i=1,2,3,4,6,12$. So, any $i$ that is a divisor of $12$ satisfies the equation $i=GCD(i,12)$.

The number of such $i$ for which $i=GCD(i,j)$ is equal to the number of divisors $d(j)$ of $j$. Since $1\le j\le n$, we need to find the count of all divisors of numbers from $1$ to $n$. In other words, we need to find the sum $d(1)+d(2)+...+d(n)$. However, calculating $d(n)$ requires factoring the number $n$, so direct computation of this sum takes $O(n)$ time.

Let's look at the sum of divisors in a different way. Among the divisors of numbers from $1$ to $n$, one appears $\lfloor \frac{n}{1}\rfloor$ times, two appears $\lfloor \frac{n}{2}\rfloor$ times, and so on (the divisor $i$ appears $\lfloor \frac{n}{i}\rfloor$ times). The number of required pairs of integers is

This sum can be computed in $O(n)$ time.

Example

For $n=6$ we have the next pairs:

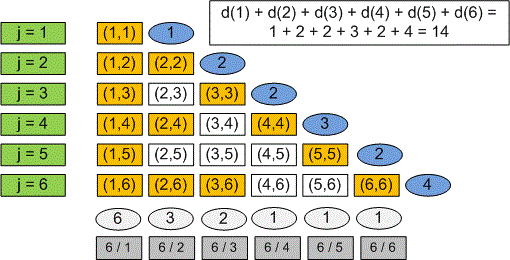
The number of pairs is

Algorithm realization

Read the value of $n$.

scanf("%d",&n);

Compute the answer using the formula and print it.

s = 0;
for(i = 1; i <= n; i++)
  s += n / i;
printf("%d\n",s);

Java realization

import java.util.*;

class Main
{
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    int n = con.nextInt();
    int s = 0;
    for(int i = 1; i <= n; i++)
      s += n / i;
    System.out.println(s);
    con.close();
  }
}

Python realization

Read the value of $n$.

n = int(input())

Compute the answer using the formula and print it.

s = 0
for i in range(1,n+1):
  s += n // i
print(s)