Editorial
Let's create an array as a counter. For each query , we'll perform two operations: and . Thus, the partial sum will equal the number of coins in the -th coin box.
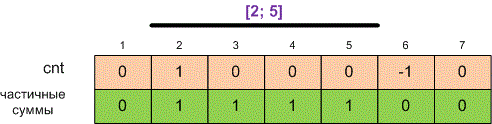
The number of days Roy performs actions is no more than . Each day he puts no more than one coin in each coin box. After completing all the actions, each coin box will contain no more than coins. Create an array of size and assign to the number of coin boxes with coins. To do this, for each partial sum execute .
Now let's find the number of coin boxes that contain at least coins. To do this, compute the partial sums in the array from right to left (that is, from the end). Then the number of coin boxes that contain at least coins equals .
Example

We get the following distribution of coins by coin boxes:

The number of coin boxes with a sum of . Partial sums (counted from right to left) indicate the number of coin boxes with at least coins.

There is one coin box with a sum of (coin box number ), two coin boxes with a sum of (coin boxes numbered and ), three coin boxes with a sum of (coin boxes numbered and ), and one coin box with a sum of (coin box number ).
After computing the partial sums of the array, it can be stated, for example, that there are coin boxes containing at least coin or that there are coin boxes containing at least coins.
Algorithm realization
Declare the arrays.
#define MAX 1000010 int cnt[MAX], coins[MAX];
Read the input data. Construct the array .
scanf("%d %d",&n,&m);
for(i = 0; i < m; i++)
{
scanf("%d %d",&l,&r);
cnt[l]++; cnt[r+1]--;
}Compute the partial sums of the array in the variable . The -th partial sum equals the number of coins in the -th coin box. equals the number of coin boxes with a sum of .
sum = 0;
for(i = 1; i <= n; i++)
{
sum += cnt[i];
coins[sum]++;
}Recompute the partial sums in the array from right to left.
for(i = MAX - 2; i >= 0; i--) coins[i] += coins[i+1];
Read the number of queries . For each query, read the value and print the answer .
scanf("%d",&q);
for(i = 0; i < q; i++)
{
scanf("%d",&x);
printf("%d\n",coins[x]);
}Python realization
Declare the lists.
MAX = 1000010 cnt = [0] * MAX coins = [0] * MAX
Read the input data.
n = int(input()) m = int(input())
Construct the list .
for _ in range(m): l, r = map(int, input().split()) cnt[l] += 1 cnt[r + 1] -= 1
Compute the partial sums of the list in the variable . The -th partial sum equals the number of coins in the -th coin box. equals the number of coin boxes with a sum of .
sum = 0 for i in range(1, n + 1): sum += cnt[i] coins[sum] += 1
Recompute the partial sums in the list from right to left.
for i in range(MAX - 2, -1, -1): coins[i] += coins[i + 1]
Read the number of queries . For each query, read the value and print the answer .
q = int(input()) for _ in range(q): x = int(input()) print(coins[x])