Editorial

Let $a [i] [j]$ be the input table. Let $d p [i] [j]$ represent the maximum sum of numbers along a path from any cell in the first row to the cell $(i, j)$ . Then

d p [i] [j] = ma x (d p [i - 1] [j - 1], d p [i - 1] [j], d p [i - 1] [j + 1]) + a [i] [j]

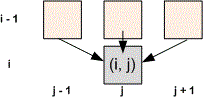
To correctly calculate the values in the first and last columns, set

d p [i] [0] = d p [i] [m + 1] = - \infty

Initialize the first row of the $d p$ array with the values from the first row of the table $a$ :

d p [1] [i] = a [1] [i], 1 \leq i \leq m

The answer to the problem will be the maximum value in the last ( $n$ -th) row of the $d p$ array.

Example

Consider the input example.

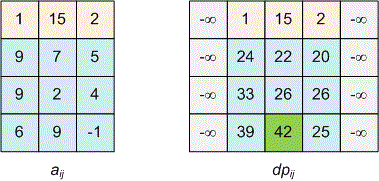
Algorithm implementation

Declare a constant $M I N$ to store the minimum value, as well as arrays $a$ and $d p$ .

#define MAX 202
#define MIN -2000000000
int a[MAX][MAX], dp[MAX][MAX];

Read the input data. The top-left corner of the table will be stored in $a [1] [1]$ . Fill the columns with indices $0$ and $m + 1$ in the $d p$ array with the minimum possible value $M I N$ .

scanf("%d %d", &n, &m);
for (i = 1; i <= n; i++)
{
  dp[i][0] = dp[i][m + 1] = MIN;
  for (j = 1; j <= m; j++)
    scanf("%d", &a[i][j]);
}

Copy the first row of array $a$ into the array $d p$ .

for (i = 1; i <= n; i++)
  dp[1][i] = a[1][i];

Recalculate the maximum sums along paths from the top row to the cell $(i, j)$ and store them in the array $d p$ .

for (i = 2; i <= n; i++)
for (j = 1; j <= m; j++)
  dp[i][j] = max(max(dp[i - 1][j - 1], dp[i - 1][j]), 
                     dp[i - 1][j + 1]) + a[i][j];

Find the largest number in the last ( $n$ -th) row of the $d p$ array.

res = MIN;
for (i = 1; i <= m; i++)
  if (dp[n][i] > res) res = dp[n][i];

Print the answer.

printf("%d\n", res);

Java implementation

import java.util.*;

public class Main
{
  static int a[][], dp[][];
  final static int MIN = -2000000000;
  
  public static void main(String[] args)
  {
    Scanner con = new Scanner(System.in);
    int n = con.nextInt();
    int m = con.nextInt();
    dp = new int[n+1][m+2];
    a = new int[n+1][m+2];
    
    for (int i = 1; i <= n; i++)
    {
      dp[i][0] = dp[i][m + 1] = MIN;
      for (int j = 1; j <= m; j++)
        a[i][j] = con.nextInt();;
    }
    
    for (int i = 1; i <= m; i++)
      dp[1][i] = a[1][i];
    
    for (int i = 2; i <= n; i++)
    for (int j = 1; j <= m; j++)
      dp[i][j] = Math.max(Math.max(dp[i - 1][j - 1], dp[i - 1][j]), dp[i - 1][j + 1]) + a[i][j];

    int res = MIN;
    for (int i = 1; i <= m; i++)
      if (dp[n][i] > res) res = dp[n][i];
    
    System.out.println(res);
    con.close();
  }
}