Metro

Algorithm Analysis

The shortest distance from the source to vertex $v$ , belonging to line $l$ , is stored in dist[v][l], where $1 \leq v \leq 70, 1 \leq l \leq 10$ . The graph is stored as adjacency lists. Along with the direction and cost of the edge, we store the number of the metro line to which the vertex, towards which the edge is directed, belongs.

We start from station $s$ , located on line $l in e 1$ . The answer to the problem is the minimum cost to reach vertex $f$ on line $l in e 2$ . When moving between vertices, a check should be performed: if the vertices belong to different lines, then 1 should be added (to make a transfer).

Using Dijkstra's algorithm, we find the shortest distances from the state ( $s$ , $l in e 1$ ) to ( $f$ , $l in e 2$ ).

Example

The graph presented in the example looks like this:

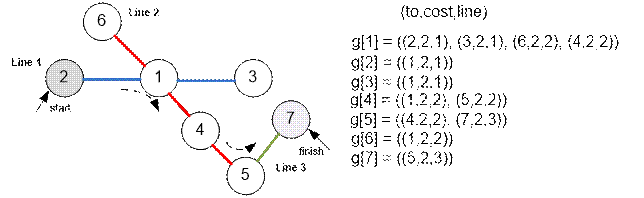
To move from station 2 to station 7, it is necessary to travel 4 segments (8 minutes) and make 2 transfers (2 minutes). The total travel time will take 10 minutes.

Algorithm Implementation

The number of vertices in the graph is no more than MAX = 71. The number of lines is no more than LINES = 11.

#define MAX 71
#define LINES 11

int dist[MAX][LINES];

struct node
{
    int to, cost, line;
    node(int to, int cost, int line) : to(to), cost(cost), line(line) {}
};

bool operator< (node a, node b)
{
    return a.cost > b.cost;
}

vector<vector<node>> g;

// Reading input data and initializing the graph

for (i = 1; i <= l; i++)
{
    scanf("%d ", &u);
    while (scanf("%d%c", &v, &ch))
    {
        g[u].push_back(node(v, 2, i));
        g[v].push_back(node(u, 2, i));
        u = v;
        if (ch == '\n') break;
    }
}

// Initializing the array of shortest distances
for (i = 1; i <= n; i++)
    for (j = 1; j <= l; j++)
        dist[i][j] = 2000000000;

// Reading information about the starting and ending stations
scanf("%d %d %d %d", &s, &line1, &f, &line2);

// Dijkstra's algorithm
dist[s][line1] = 0;
priority_queue<node, vector<node>> pq;
pq.push(node(s, 0, line1)); // (v, cost, line)

while (!pq.empty())
{
    int cost = pq.top().cost;
    int v = pq.top().to;
    int l1 = pq.top().line;
    pq.pop();

    for (i = 0; i < g[v].size(); i++)
    {
        int to = g[v][i].to;
        int w = g[v][i].cost;
        int l2 = g[v][i].line;
        int tot_cost = cost + w;
        if (l1 != l2) tot_cost += 1;
        if (tot_cost < dist[to][l2])
        {
            dist[to][l2] = tot_cost;
            pq.push(node(to, tot_cost, l2));
        }
    }
}

// Outputting the answer
printf("%d\n", dist[f][line2]);