Editorial

Each query $S_{l, r}$ can be performed using a loop with a complexity of $O (n)$ . We have $m \leq 1 0^{6}$ queries and the length of the array is $n \leq 1 0^{6}$ . If each query runs in linear time, we would need no more than $n \times m \leq 1 0^{12}$ operations, which will exceed the Time Limit.

Consider the partial sums of array $a$ :

s_{1} = a_{1}; s_{2} = a_{1} + a_{2}; s_{3} = a_{1} + a_{2} + a_{3}; ... s_{n} = a_{1} + a_{2} + a_{3} + ... + a_{n};

It is possible to compute the values $s_{1}, s_{2}, ..., s_{n}$ in a linear array $s$ in $O (n)$ time.

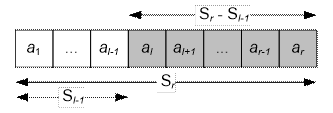
Further note that

S_{l, r} = a_{l} + a_{l + 1} + ... + a_{r} = (a_{1} + ... + a_{l} + a_{l + 1} + ... + a_{r}) - (a_{1} + ... + a_{l - 1}) = s_{r} - s_{l - 1}

So we can answer the query $S_{l, r}$ in constant time.

Example

Let's compute the sum $a_{3} + a_{4} + a_{5}$ for the input example.

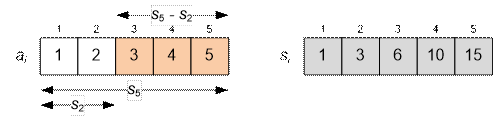
We have: $a_{3} + a_{4} + a_{5} = s_{5} - s_{2} = 15 - 3 = 12.$

Algorithm realization

Declare two working two-dimensional arrays.

#define MAX 1000001
int a[MAX], s[MAX];

Read the input set of numbers into array $a$ , and calculate the partial sums in array $s$ .

scanf("%d",&n); 
s[0] = 0;
for(i = 1; i <= n; i++)
{
  scanf("%d",&a[i]);
  s[i] = s[i-1] + a[i];
}

Process $m$ queries.

scanf("%d",&m);
for(i = 0; i < m; i++)
{
  scanf("%d %d",&b,&c);
  printf("%d\n",s[c] - s[b-1]);
}

Python realization

Read the input data.

n = int(input())
a = [0] + list(map(int, input().split()))

Calculate the partial sums of list $a$ in list $s$ .

s = [0] * (n + 1)
for i in range(1, n + 1):
  s[i] = s[i - 1] + a[i]

Process $m$ queries.

m = int(input())
for _ in range(m):
  b, c = map(int, input().split())
  print(s[c] - s[b - 1])